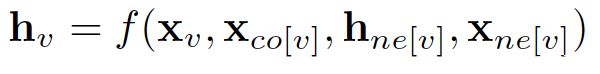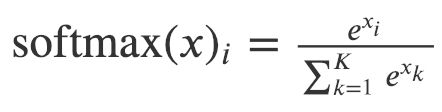GNN

图形神经网络（GNN）主要用于分子应用，因为分子结构可以用图形结构表示。 GNN的有趣之处在于它可以有效地建模系统中对象之间的关系或交互。

近年来，图神经网络(GNN)在社交网络、知识图、推荐系统甚至生命科学等各个领域得到了越来越广泛的应用。GNN在对图节点之间依赖关系进行建模的强大功能，使得与图分析相关的研究领域取得了突破。本文介绍了图神经网络的基本原理，以及两种高级的算法，DeepWalk和GraphSage。

图(Graph)

在讨论GNN之前，我们先来了解一下什么是图。在计算机科学中，图是由顶点和边两部分组成的一种数据结构。图G可以通过顶点集合V和它包含的边E来进行描述。

根据顶点之间是否存在方向依赖关系，边可以是有向的，也可以是无向的。

图 1有向图

顶点也称为节点,在本文中，这两个术语是可以互换。

图神经网络

图神经网络是一种直接作用于图结构上的神经网络。GNN的一个典型应用是节点分类,本质上，图中的每个节点都与一个标签相关联，我们希望预测未标记节点的标签。本文将介绍该论文中描述的算法,

在节点分类问题中，每个节点v都可以用其特征x_v表示并且与已标记的标签t_v相关联。给定部分标记的图G，目标是利用这些标记的节点来预测未标记的节点标签。它通过学习得到每个节点的d维向量（状态）表示为h_v，同时包含其相邻节点的信息。

x_co[v] 代表连接顶点v的边的特征，h_ne[v]代表顶点v的邻居节点的嵌入表示，x_ne[v]代表顶点v的邻居节点特征。f是将输入投影到d维空间的转移函数,由于要求出h_v的唯一解，我们应用Banach不动点理论重写上述方程进行迭代更新。

H和X分别表示所有h和x的连接,通过将状态h_v以及特征x_v传递给输出函数g来计算GNN的输出。

这里的f和g都可以解释为全连接前馈神经网络,L1损失可以直接表述为如下函数：

它可以通过梯度下降进行优化，但是该论文指出的原始GNN有三个主要局限：

1.如果放宽了“固定点”的假设，则可以利用多层感知器来学习更稳定的表示，并删除迭代更新过程。 这是因为在原始方法中，不同的迭代使用转移函数f的相同参数，而不同MLP层中的不同参数允许分层特征提取；

2.不能处理边缘信息（例如知识图谱中的不同边可能表示节点之间的不同关系）；

3. 固定点会限制节点分布的多样化，因此可能不适合学习节点表示。

虽然现在已经提出了几种GNN变体来解决上述问题。 但是他们不是论文的重点。

DeepWalk

DeepWalk是第一个以无监督学习的节点嵌入算法。它在训练过程中类似于词嵌入。它的目的是让图中的节点分布和语料库中的单词分布都遵循幂律，如下图所示：

算法包括两个步骤：

1. 在图中的节点上执行随机游走生成节点序列;

2. 运行skip-gram，根据步骤1中生成的节点序列学习每个节点的嵌入;

在随机游走过程中，下一个节点是从前一节点的邻居统一采样。然后将每个序列截短为长度为2 | w |+1的子序列，其中w表示skip-gram中的窗口大小。如果您不熟悉skip-gram，我之前的博客文章已经向您介绍它的工作原理。

在论文中，分层softmax用于解决由于节点数量庞大而导致的softmax计算成本过高的问题。为了计算每个单独输出元素的softmax值，我们必须为所有元素k计算ek。

图 2 softmax的定义

因此，原始softmax的计算时间是 O(|V|) ，其中其中V表示图中的顶点集。

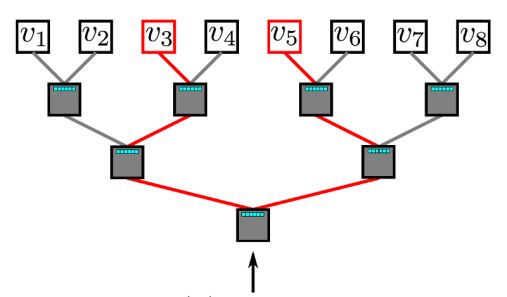
多层的softmax利用二叉树来解决softmax计算成本问题。 在二叉树中，所有叶子节点（上面所说的图中的v1，v2，... v8）都是图中的顶点。 在每个内部节点中（除了叶子节点以外的节点，也就是分枝结点），都通过一个二元分类器来决定路径的选取。 为了计算某个顶点v_k的概率，可以简单地计算沿着从根节点到叶子节点v_k的路径中的每个子路径的概率。 由于每个节点的孩子节点的概率和为1，因此在多层softmax中，所有顶点的概率之和等于1的特性仍然能够保持。如果n是叶子的数量，二叉树的最长路径由O（log（n））限定，因此，元素的计算时间复杂度将减少到O（log | V |）。

图 3多层softmax

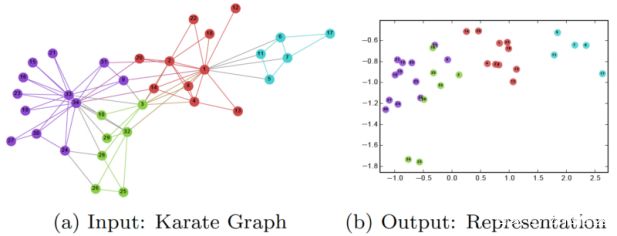
在训练DeepWalk GNN之后，模型已经学习到了每个节点的表示，如下图所示。不同的颜色在输入图中（图a）表示不同标签。 我们可以看到，在输出图中，具有相同标签的节点聚集在一起，而具有不同标签的大多数节点被正确分开。

然而，DeepWalk的主要问题是它缺乏泛化能力。每当有新节点加入到图中时，它必须重新训练模型以正确表示该节点。因此，这种GNN不适用于图中节点不断变化的动态图。

GraphSage

GraphSage提供了解决上述问题的方案，它以归纳方式学习每个节点的嵌入。具体来讲，它将每个节点用其邻域的聚合重新表示。因此，即使在训练期间未出现的新节点，也仍然可以由其相邻节点正确地表示。下图展示了GraphSage的算法过程：

外层for循环表示更新迭代次数，而 h^k_v 表示节点v在迭代第 k次时的本征向量。在每次迭代时，将通过聚合函数，前一次迭代中v和v领域的本征向量以及权重矩阵W^k来更新h^k_v。这篇论文提出了三种聚合函数：

1.均值聚合器：

均值聚合器取一个节点及其邻域的本征向量的平均值。

 

与原始方程相比，它删除了上述伪代码中第5行的连接操作。这种操作可以被视为"skip-connection" ("跳连接")，这篇论文后面将证明其可以在很大程度上提高模型的性能。

2. LSTM聚合器：

由于图中的节点没有任何顺序，因此他们通过互换这些节点来随机分配顺序。

3.池聚合器：

此运算符在相邻顶点集上执行逐元素池化函数。下面显示了最大池的例子：

可以用平均池或任何其他对称池函数替换这种最大池函数。尽管均值池和最大池聚合器性能相似，但是池聚合器（也就是说采用最大池函数）被实验证明有最佳的性能。 论文使用max-pooling作为默认聚合函数。损失函数定义如下：

其中u 和v 共同出现在一定长度的随机游走中，而 v_n 是不与u共同出现的负样本。这种损失函数鼓动节点在投影空间中更靠近嵌入距离更近的节点，而与那些相距很远的节点分离。通过这种方法，节点将获得越来越多其邻域的信息。

GraphSage通过聚合其附近的节点，可以为看不见的节点生成可表示的嵌入位置。它让节点嵌入的方式可以被应用于涉及动态图的研究领域，这类动态图的图的结构是可以不断变化的。例如，Pinterest采用了GraphSage的扩展版本PinSage作为他们的内容探索系统的核心。