卷积

n次多项式 f(x) = [ a0, a1, …, an-1 ]
卷积c(x) = a(x) ⊗ b(x), ci = Σ aj * bi-j

n次多项式可以用n个点来唯一表示，即点值表达式。
范德蒙行列式 * 系数向量 = Y向量

a(x) 表示为

b(x)表示为

c(x)表示为

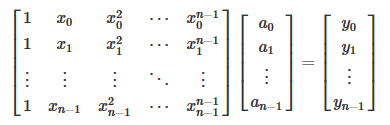
一、hdu 1402

#include
#include
#include
#include
using namespace std;

const int _=200020;
namespace G
{
    const double pi=acos(-1.0);
    struct CX
    {
        double a,b;
        CX(double a=0,double b=0):a(a),b(b){}
        CX operator+(const CX& x)
        {
            return CX(a+x.a,b+x.b);
        }
        CX operator-(const CX& x)
        {
            return CX(a-x.a,b-x.b);
        }
        CX operator*(const CX& x)
        {
            return CX(a*x.a-b*x.b,a*x.b+b*x.a);
        }
    };
    /// 二进制平摊反转
    void swap(CX y[],int len)
    {
        for(int i=1,j=len/2; i1; i++)
        {
            if(istd::swap(y[i],y[j]);
            int k=len/2;
            while(j>=k)
                j-=k,k/=2;
            if(jvoid fft(CX y[],int len,int on)
    {
        swap(y,len);
        for(int i=2; i<=len; i<<=1)
        {
            double x=2*pi*on/i; ///
            CX w(cos(x),sin(x));
            for(int j = 0; j < len; j += i) ///
            {
                CX e(1,0);
                for(int k=j; k2; k++)
                {
                    CX u=y[k];
                    CX v=e*y[k+i/2];
                    y[k]=u+v;
                    y[k+i/2]=u-v;
                    e=e*w;
                }
            }
        }
        if(on==-1)
        {
            for(int i=0;iint sum[_];
    char str1[_],str2[_];
    void go()
    {
        while(~scanf("%s%s",str1,str2))
        {
            int L1=strlen(str1);
            int L2=strlen(str2);
            int len=1;
            while(len2 || len2)len<<=1;
            memset(x1,0,sizeof x1);
            for(int i=0;i1-i]-'0',0);
            }
            memset(x2,0,sizeof x2);
            for(int i=0;i1-i]-'0',0);
            }
            fft(x1,len,1);
            fft(x2,len,1);
            for(int i=0;i1);
            for(int i=0;i0.5;
            for(int i=0;i1]+=sum[i]/10;
                sum[i]%=10;
            }
            len=L1+L2-1;
            while(sum[len]<=0 && len>0)len--;
            for(int i=len;i>=0;i--)
                printf("%c",sum[i]+'0');
            puts("");
        }
    }
}
int main()
{
    G::go();
}

二、

#include
#include
#include
#include
#include
#define ll long long
using namespace std;
const ll _=100010;
const ll mod=998244353;

ll n,a[_];

ll fpow(ll p,ll q)
{
    if(q<0)p=fpow(p,mod-2),q=-q;
    ll ret=1;
    while(q)
    {
        if(q&1)ret=ret*p%mod;
        p=p*p%mod;
        q>>=1;
    }
    return ret;
}
namespace G
{
    /// 二进制平摊反转
    void swap(ll y[],ll len)
    {
        for(ll i=1,j=len/2; i1; i++)
        {
            if(iy[i],y[j]);
            ll k=len/2;
            while(j>=k)
                j-=k,k/=2;
            if(jy[],ll len,ll on)
    {
        swap(y,len);
        for(ll i=2; i<=len; i<<=1)
        {
            //double x=2*pi*on/i; ///
            //CX w(cos(x),sin(x));
            ll w = fpow(3,on*(mod-1)/i);
            for(ll j = 0; j < len; j += i) ///
            {
                //CX e(1,0);
                ll e = 1;
                for(ll k=j; k2; k++)
                {
                    //CX u=y[k];
                    ll u=y[k];
                    //CX v=e*y[k+i/2];
                    ll v=e*y[k+i/2]%mod;
                    //y[k]=u+v;
                    y[k]=(u+v)%mod;
                    //y[k+i/2]=u-v;
                    y[k+i/2]=(u-v+mod)%mod;
                    //e=e*w;
                    e=e*w%mod;
                }
            }
        }
        if(on==-1)
        {
            ll tmp=fpow(len,-1);
            for(ll i=0;iy[i].a/=len;
                y[i]=y[i]*tmp%mod;
        }
    }

    ll x1[_<<2],x2[_<<2];
    ll fac[_],fav[_],two[_],twv[_];
    ll bit[_];
    void Init()
    {
        fac[0]=1;
        for(ll i=1;i<_;i++)
            fac[i]=i*fac[i-1]%mod;
        for(ll i=0;i<_;i++)
            fav[i]=fpow(fac[i],-1);
        two[0]=1;
        for(ll i=1;i<_;i++)
            two[i]=two[i-1]*2%mod;
        for(ll i=0;i<_;i++)
            twv[i]=fpow(two[i],-1);
    }
    void go()
    {
        Init();
        ll cas;scanf("%I64d",&cas);
        while(cas--)
        {
            scanf("%I64d",&n);
            for(ll i=1;i<=n;i++)
                scanf("%I64d",&a[i]);
            sort(a+1,a+n+1,greater());
            for(ll i=0;i<=n;i++)
            {
                x1[i] = two[n-i]*fav[i]%mod;
                x2[i] = a[i]*(i>0 ? fac[i-1] : 0)%mod;
            }
            reverse(x2,x2+n+1);
            ll len=1;
            while(len <= 2*(n+1)) len<<=1;
            for(ll i=n+1;i0;
            fft(x1,len,1);
            fft(x2,len,1);
            for(ll i=0;i*x2[i]%mod;
            fft(x1,len,-1);
            for(ll i=1;i<=n;i++)
                bit[i] = (bit[i-1] + x1[n-i]*twv[i]%mod * fav[i-1]%mod)%mod;
            for(ll i=1;i<=n;i++)
                printf("%I64d ",bit[i]);
            puts("");
        }
    }
}

int main()
{
    G::go();
}