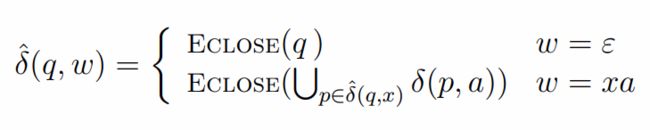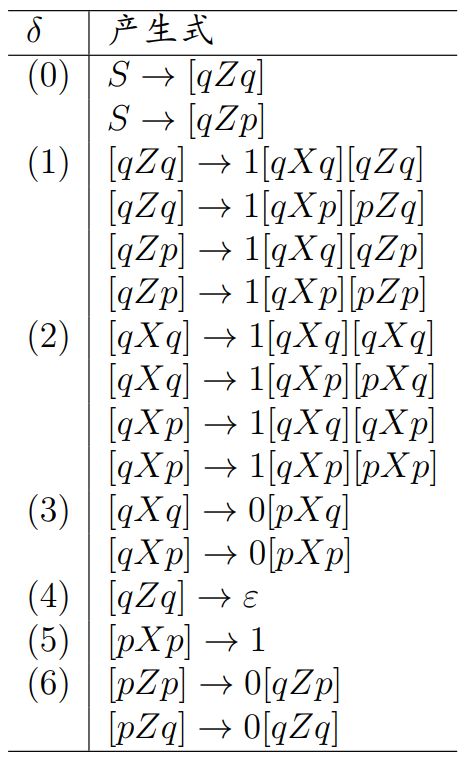形式语言与自动机总结笔记
形式语言与自动机
- MOOC:形式语言与自动机理论
- GitHub课件资源:gzn00417/2020Spring-Formal-Languages-and-Automata
教学大纲
- 正则语言
- 2 有穷自动机
2.1 确定的有穷自动机
2.2 非确定有穷自动机
2.3 带有空转移的非确定有穷自动机 - 3 正则表达式
3.1 正则表达式
3.2 自动机和正则表达式
3.3 正则表达式的代数定律 - 4 正则语言的性质
4.1 正则语言的泵引理
4.2 正则语言的封闭性
4.3 正则语言的判定性质
4.4 自动机最小化
- 2 有穷自动机
- 上下文无关语言
- 5 上下文无关文法
5.1 上下文无关文法
5.2 语法分析树
5.3 文法和语言的歧义性
5.4 文法的化简和范式 - 6 下推自动机
6.1 下推自动机
6.2 下推自动机的语言
6.3 下推自动机与文法的等价性
6.4 确定性下推自动机 - 7 上下文无关语言的性质
7.1 上下文无关语言的泵引理
7.2 上下文无关语言的封闭性
7.3 上下文无关语言的判定性质
- 5 上下文无关文法
- 计算导论
- 8.1 图灵机及其扩展
- 8.2 不可判定性
主要考点
- 构造自动机:DFA、NFA、ε-NFA、PDA、DPDA、TM
- 设计正则表达式/正则文法、上下文无关文法
- 泵引理+封闭性证明不是正则语言
- 等价性转换
- NFA和DFA
- FA和正则表达式
- PDA和CFG
- CNF和GNF
- 语言的接受和设计
文章目录
- 形式语言与自动机
- 教学大纲
- 主要考点
- 1. 确定的有穷自动机(DFA)
- 2. 非确定的有穷自动机(NFA)
- 3. 带有空转移的非确定有穷自动机(ε-NFA)
- 4. DFA和NFA的等价性与转换
- 5. DFA化简:状态等价性和填表算法
- 5.1 等价和可区分
- 5.2 填表算法 Table-Filling Algorithm
- 6. 正则表达式(Regular Express)
- 7. 正则表达式和有穷自动机的等价关系与转换
- 7.1 正则表达式-->自动机
- 7.1.1 并(加号)的转换
- 7.1.2 幂(星号)的转换
- 7.2 自动机-->正则表达式
- 7.2.1 删除状态法
- 7.2.2 归纳法
- 8. 正则语言的性质
- 8.1 泵引理
- 8.2 封闭性
- 9. 上下文无关文法(CFG)
- 9.1 规约
- 9.2 派生
- 9.3 解析树
- 9.4 歧义
- 10. 上下文无关文法的化简
- 10.1 消除无用符号
- 10.2 消除ε产生式
- 10.3 消除单元产生式
- 11. 上下文无关文法的范式
- 11.1 乔姆斯基范式(CNF)
- 11.2 格雷巴赫范式(GNF)
- 12. 下推自动机(PDA)
- 12.1 瞬时描述(ID)
- 12.1.1 转移
- 12.2 下推自动机接受的语言(终态/空栈)
- 13. CFG ⟺ \Longleftrightarrow ⟺PDA(等价性)
- 13.1 CFG ⟹ \Longrightarrow ⟹PDA
- 13.2 PDA ⟹ \Longrightarrow ⟹CFG
- 14. GNF ⟹ \Longrightarrow ⟹PDA
- 15. 确定性下推自动机(DPDA)
- 16 上下文无关语言的泵引理
- 17 上下文无关语言的封闭性
- 17.1 代换
- 17.2 封闭性应用
- 18 上下文无关语言的判定性质
- 18.1 可判定的 CFL 问题
- 18.2 CYK算法
- 18.3 不可判定的 CFL 问题
- 19. 图灵机
- 19.1 瞬时描述(ID)
- 19.2 递归可枚举语言
- 19.3 真减法
- 19.4 乘法
1. 确定的有穷自动机(DFA)
确定的有穷自动机(DFA, Deterministic Finite Automaton) A 为五元组
A = ( Q , Σ , δ , q 0 , F ) A = (Q, Σ, δ, q0, F) A=(Q,Σ,δ,q0,F)
- Q Q Q : 有穷状态集;
- Σ Σ Σ : 有穷输入符号集或字母表;
- δ δ δ : Q × Σ → Q Q × Σ → Q Q×Σ→Q, 状态转移函数;
- q 0 q^0 q0 ∈ Q : 初始状态;
- F ⊆ Q F ⊆ Q F⊆Q : 终结状态集或接受状态集.
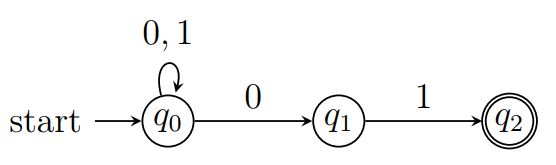
例:请设计 DFA, 在任何由 0 和 1 构成的串中, 接受含有 01 子串的全部串.
- 未发现 01, 即使 0 都还没出现过;
- 未发现 01, 但刚刚读入字符是 0;
- 已经发现了 01
因此 DFA A 的可定义为:
A = ( { q 1 , q 2 , q 3 } , { 0 , 1 } , δ , q 1 , { q 3 } ) A\ = \ (\{ q1,\ q2,\ q3\},\ \{ 0,\ 1\},\ \delta,\ q1,\ \{ q3\}) A = ({q1, q2, q3}, {0, 1}, δ, q1, {q3})
-
其中 δ 为:
δ ( q 1 , 1 ) = q 1 δ(q1, 1) = q1 δ(q1,1)=q1
δ ( q 2 , 1 ) = q 3 δ(q2, 1) = q3 δ(q2,1)=q3
δ ( q 3 , 1 ) = q 3 δ(q3, 1) = q3 δ(q3,1)=q3
δ ( q 1 , 0 ) = q 2 δ(q1, 0) = q2 δ(q1,0)=q2
δ ( q 2 , 0 ) = q 2 δ(q2, 0) = q2 δ(q2,0)=q2
δ ( q 3 , 0 ) = q 3 δ(q3, 0) = q3 δ(q3,0)=q3 -
- 每个状态 q 对应一个节点, 用圆圈表示;
- 状态转移 δ(q, a) = p 为一条从 q 到 p 且标记为字符 a 的有向边;
- 开始状态 q0 用一个标有 start 的箭头表示;
- 接受状态的节点, 用双圆圈表示.
2. 非确定的有穷自动机(NFA)
非确定有穷自动机(NFA, Nondeterministic Finite Automaton) A 为五元组
A = ( Q , Σ , δ , q 0 , F ) A = (Q, Σ, δ, q0, F) A=(Q,Σ,δ,q0,F)
- Q Q Q : 有穷状态集;
- Σ Σ Σ : 有穷输入符号集或字母表;
- δ δ δ : Q × Σ = 2 Q Q \times \Sigma = 2^{Q} Q×Σ=2Q, 状态转移函数;
- q 0 q^0 q0 ∈ Q : 初始状态;
- F ⊆ Q F ⊆ Q F⊆Q : 终结状态集或接受状态集.
与DFA区别
- δ δ δ : Q × Σ = 2 Q Q \times \Sigma = 2^{Q} Q×Σ=2Q
- 转移后为一个状态集合
- 同一个状态在相同的输入下,可以有多个转移状态
- 自动机可以处在多个当前状态
例:接受全部以 01 结尾的串的 NFA.
解:五元组为 A = ( { q 0 , q 1 , q 2 } , { 0 , 1 } , δ , q 0 , { q 2 } ) A\ = \ (\{ q0,\ q1,\ q2\},\ \{ 0,\ 1\},\ \delta,\ q0,\ \{ q2\}) A = ({q0, q1, q2}, {0, 1}, δ, q0, {q2})
转移函数 δ:
- δ ( q 0 , 0 ) = { q 0 , q 1 } \delta(q0,\ 0)\ = \ \{ q0,\ q1\} δ(q0, 0) = {q0, q1}
- δ ( q 1 , 0 ) = ∅ \delta(q1,\ 0)\ = \ \varnothing δ(q1, 0) = ∅
- δ ( q 2 , 0 ) = ∅ \delta(q2,\ 0)\ = \ \varnothing δ(q2, 0) = ∅
- δ ( q 0 , 1 ) = { q 0 } \delta(q0,\ 1)\ = \ \{ q0\} δ(q0, 1) = {q0}
- δ ( q 1 , 1 ) = { q 2 } \delta(q1,\ 1)\ = \ \{ q2\} δ(q1, 1) = {q2}
- δ ( q 2 , 1 ) = ∅ \delta(q2,\ 1)\ = \ \varnothing δ(q2, 1) = ∅
3. 带有空转移的非确定有穷自动机(ε-NFA)
DFA、NFA和ε-NFA性质:
- 自动机在某状态, 读入某个字符时, 可能有多个转移
- 自动机在某状态, 读入某个字符时, 可能没有转移
- 自动机在某状态, 可能不读入字符, 就进行转移
ε-NFA与NFA
- 不读入字符,就进行转移的NFA
- Q × ( Σ ∪ { ε } ) = 2 Q Q \times (\Sigma \cup \left\{ \varepsilon \right\}) = 2^{Q} Q×(Σ∪{ε})=2Q
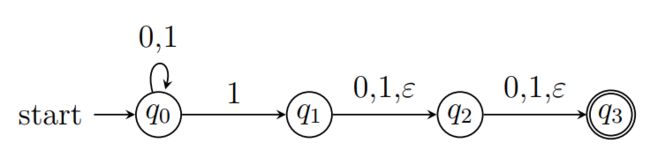
例:语言 L = w ∈ 0 , 1 ∗ ∣ w 倒 数 3 个 字 符 至 少 有 一 个 是 1 L = {w ∈ {0, 1}∗ | w 倒数 3 个字符至少有一个是 1} L=w∈0,1∗∣w倒数3个字符至少有一个是1 的ε-NFA.
此后, 不再明确区分 ε-NFA 和 NFA, 而认为它们都是 NFA.
4. DFA和NFA的等价性与转换
ε − 闭 包 : q 0 → 所 有 q 0 能 到 达 的 状 态 的 集 合 ε-闭包: {q_0} → {所有q_0能到达的状态的集合} ε−闭包:q0→所有q0能到达的状态的集合
记为 E c l o s e ( q ) Eclose(q) Eclose(q)
例:求以下状态的 ε − c l o s u r e ε - closure ε−closure
解:
- E ( 1 ) = { 1 , 2 , 4 , 3 , 6 } E(1) = \{ 1, 2, 4, 3, 6 \} E(1)={1,2,4,3,6}
- E ( 2 ) = { 2 , 3 , 6 } E(2) = \{ 2, 3, 6 \} E(2)={2,3,6}
- E ( 3 ) = { 3 , 6 } E(3) = \{ 3, 6 \} E(3)={3,6}
- E ( 4 ) = { 4 } E(4) = \{ 4 \} E(4)={4}
- E ( 5 ) = { 5 , 7 } E(5) = \{ 5, 7 \} E(5)={5,7}
- E ( 6 ) = { 6 } E(6) = \{ 6 \} E(6)={6}
- E ( 7 ) = { 7 } E(7) = \{ 7 \} E(7)={7}
解:
- 状态转移表和ε-闭包为

- 设置初状态 { q 0 } \{q_0 \} {q0}
- 当输入0时, { q 0 } → { q 0 } \{q_0\} → \{q_0\} {q0}→{q0},不变,则 { q 0 } \{q_0\} {q0}的ε-闭包还是为 { q 0 } \{q_0\} {q0}
- 当输入1时, { q 0 } → { q 0 , q 1 } \{q_0\} → \{q_0, q_1\} {q0}→{q0,q1},则 { q 0 , q 1 } \{q_0, q_1\} {q0,q1}的ε-闭包为 { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3}
- 因此状态转移函数如下
| 0 0 0 | 1 1 1 | |
|---|---|---|
| { q 0 } \{q_0\} {q0} | { q 0 } \{q_0\} {q0} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3} |
- 出现新状态 { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3}
- 当输入0时, { q 0 , q 1 , q 2 , q 3 } → { q 0 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} → \{q_0, q_2, q_3\} {q0,q1,q2,q3}→{q0,q2,q3},则 { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3}的ε-闭包为 { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3}
- 当输入1时, { q 0 , q 1 , q 2 , q 3 } → { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} → \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3}→{q0,q1,q2,q3},则 { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3}的ε-闭包为 { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3}
- 因此状态转移函数如下
| 0 0 0 | 1 1 1 | |
|---|---|---|
| { q 0 } \{q_0\} {q0} | { q 0 } \{q_0\} {q0} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3} | { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
- 出现新状态 { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3}
- 当输入0时, { q 0 , q 2 , q 3 } → { q 0 , q 3 } \{q_0, q_2, q_3\} → \{q_0, q_3\} {q0,q2,q3}→{q0,q3},则 { q 0 , q 3 } \{q_0, q_3\} {q0,q3}的ε-闭包为 { q 0 , q 3 } \{q_0, q_3\} {q0,q3}(红色为原转移,绿色为转移后的闭包)

- 当输入1时, { q 0 , q 2 , q 3 } → { q 0 , q 1 , q 2 , q 3 } \{q_0, q_2, q_3\} → \{q_0, q_1, q_2, q_3\} {q0,q2,q3}→{q0,q1,q2,q3},则 { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3}的ε-闭包为 { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3}
- 当输入0时, { q 0 , q 2 , q 3 } → { q 0 , q 3 } \{q_0, q_2, q_3\} → \{q_0, q_3\} {q0,q2,q3}→{q0,q3},则 { q 0 , q 3 } \{q_0, q_3\} {q0,q3}的ε-闭包为 { q 0 , q 3 } \{q_0, q_3\} {q0,q3}(红色为原转移,绿色为转移后的闭包)
- 因此状态转移函数如下
| 0 0 0 | 1 1 1 | |
|---|---|---|
| { q 0 } \{q_0\} {q0} | { q 0 } \{q_0\} {q0} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3} | { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3} | { q 0 , q 3 } \{q_0, q_3\} {q0,q3} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
- 出现新状态 { q 0 , q 3 } \{q_0, q_3\} {q0,q3}
- 同理,因此状态转移函数如下
| 0 0 0 | 1 1 1 | |
|---|---|---|
| { q 0 } \{q_0\} {q0} | { q 0 } \{q_0\} {q0} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3} | { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3} | { q 0 , q 3 } \{q_0, q_3\} {q0,q3} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| { q 0 , q 3 } \{q_0, q_3\} {q0,q3} | { q 0 } \{q_0\} {q0} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
- 最后,将 q 0 q_0 q0设为初始状态,且将含有原转移终止符( q 3 q_3 q3)的状态设置为终止状态,即 { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1,q_2, q_3\} {q0,q1,q2,q3}、 { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3}、 { q 0 , q 3 } \{q_0, q_3\} {q0,q3}均为终止状态
| 0 0 0 | 1 1 1 | |
|---|---|---|
| → { q 0 } →\{q_0\} →{q0} | { q 0 } \{q_0\} {q0} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| ∗ { q 0 , q 1 , q 2 , q 3 } * \{q_0, q_1,q_2, q_3\} ∗{q0,q1,q2,q3} | { q 0 , q 2 , q 3 } \{q_0, q_2, q_3\} {q0,q2,q3} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| ∗ { q 0 , q 2 , q 3 } * \{q_0, q_2, q_3\} ∗{q0,q2,q3} | { q 0 , q 3 } \{q_0, q_3\} {q0,q3} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
| ∗ { q 0 , q 3 } * \{q_0, q_3\} ∗{q0,q3} | { q 0 } \{q_0\} {q0} | { q 0 , q 1 , q 2 , q 3 } \{q_0, q_1, q_2, q_3\} {q0,q1,q2,q3} |
5. DFA化简:状态等价性和填表算法
5.1 等价和可区分
对于任意两个状态,一定是
- 等价
- 可区分
二者之一
-
- 即:当两个状态为等价时,对于任意一个输入符,转移状态同时为终止状态或同时不是;
- 注:不一定相同
- 因此:不提及两个状态的转移状态是否相同
- 即:当两个状态为等价时,对于任意一个输入符,转移状态同时为终止状态或同时不是;
-
- 即:当两个状态为可区分时(不等价),存在至少一个输入符,转移状态不同时为终止(不同时为非终止)
5.2 填表算法 Table-Filling Algorithm
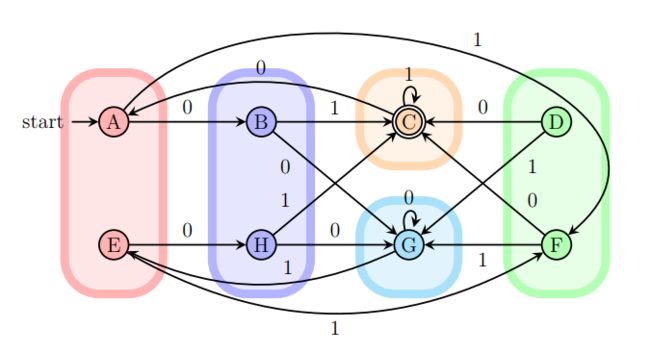
- 直接标记终态和非终态之间的状态对
- 标记所有经过字符 0 到达终态和非终态的状态对
- {D, F }×{A, B, C, E, G, H}- 标记所有经过字符 1 到达终态和非终态的状态对
- {B, H }×{A, C, D, E, F, G}- 此时还有 [A,E], [A,G], [B,H], [D,F], [E,G] 未标记, 只需逐个检查.
- [A,G] 是可区分的, 因为经串 01 到可区分的 [C,E];
- [E,G] 是可区分的, 因为经串 10 到可区分的 [C,H].- [A,E], [B,H] 和 [D,F] 在经过很短的字符串后, 都会到达相同状态,因此都是等价的.
6. 正则表达式(Regular Express)
语言是字符串集合。
语言的运算:并、连接、幂、克林闭包
递归定义:
如果E为字母表,则2上的正则表达式递归定义为:
- 0是一个正则表达式,表示空语言;
- ε ε ε是一个正则表达式,表示语言{e};
- 任意 a ∈ E a∈E a∈E,a是一个正则表达式,表示语言{a};
- 如果正则表达式 r 和 s 分别表示语言 R R R和 S S S,那么 r + s , r s , r ∗ 和 ( r ) r+s,rs, r^*和 ( r ) r+s,rs,r∗和(r)都是正则表达式
- 分别表示语言 R ∪ S , R ⋅ S , R ∗ 和 R R∪S,R·S,R*和R R∪S,R⋅S,R∗和R
优先级:括号>星(*)>连接(×)>加(+)
例:L = {w | w ∈ {0, 1}∗ and w has no pair of consecutive 0’s.}
- 解:1∗(011∗)∗(0 + ε) 或 (1 + 01)∗(0 + ε)
7. 正则表达式和有穷自动机的等价关系与转换
7.1 正则表达式–>自动机
正则表达式到自动机的转换分为以下4种
- 连接(乘法)
- 并(加法)
- 幂(星)
- 闭包
例:正则表达式 ( 0 + 1 ) ∗ 1 ( 0 + 1 ) (0+1)^*1(0+1) (0+1)∗1(0+1)转换为 ε − N F A ε-NFA ε−NFA
7.1.1 并(加号)的转换
7.1.2 幂(星号)的转换
例: ( 0 + 1 ) ∗ (0+1)^* (0+1)∗
7.2 自动机–>正则表达式
若干例题
- 通过7.1的逆向推导得出
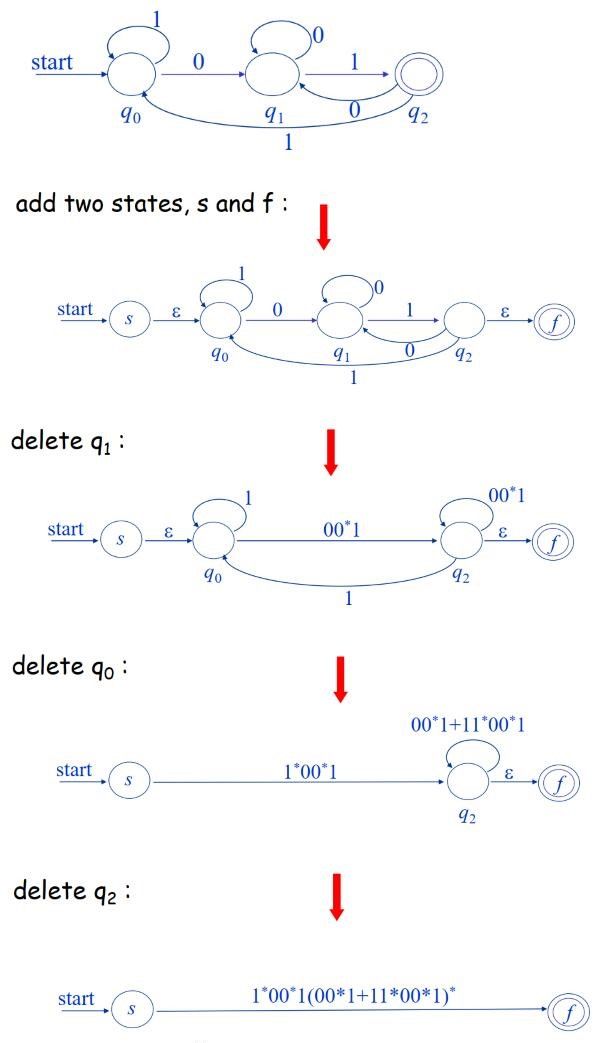
7.2.1 删除状态法
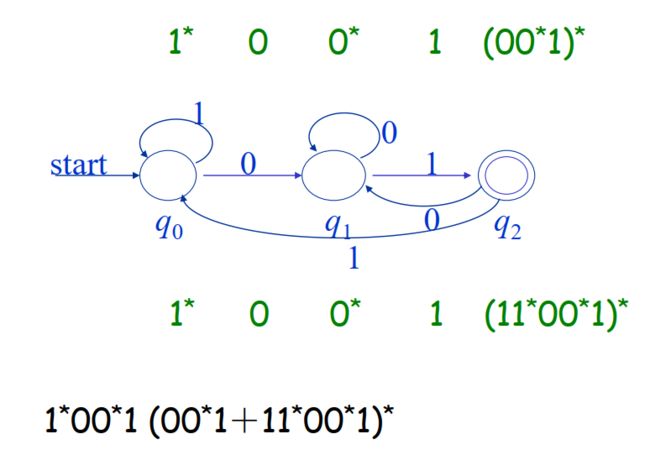
7.2.2 归纳法
- Pick every label on the path from q 0 q_0 q0 to q 2 q_2 q2 ---- one by one
- Form every R e g E x p RegExp RegExp on the path from q 0 q_0 q0 to q 2 q_2 q2 ---- one by one
R i j ( k ) : 0 < = k < = n R_{ij}^{(k)}: 0<=k<=n Rij(k):0<=k<=n: i i i到 j j j路径上的正则表达式
- no inner node is greater than k
8. 正则语言的性质
8.1 泵引理
- 确定一个语言是正则语言?
- 是
- DFA
- NFA
- ε-NFA
- 正则表达式
- 否
- 泵引理,反证法
- 是
即:前 N N N的字符中存在一段可以在该位置循环出现
泵引理只是正则语言的必要条件,只能用来证明某个语言不是正则的
8.2 封闭性
正则语言经某些运算后得到的新语言仍保持正则,称正则语言在这些运算下封闭
正则语言 L 和 M, 在这些运算下封闭
- 并: L ∪ M L \cup M L∪M
- 连接: L M LM LM
- 闭包: L ∗ L^* L∗
- 补: L ‾ \overline{L} L
- 差: L − M L-M L−M
- 交: L ∩ M L \cap M L∩M
- 反转: L R = { w R ∣ w ϵ L } L^{R} = \left\{ w^{R}|w\epsilon L \right\} LR={wR∣wϵL}
- 同态
- 逆同态
考点:能够运用这些性质,结合泵引理证明一个语言是否是正则语言
自动机的转换
- 并:使用 ε − N F A ε-NFA ε−NFA,新建初始状态节点,空转移到原来的初始状态;
- 连接:前者终止状态空转移到后者初始状态;
- 闭包:增加新终止状态,原终止状态空转移到新终止状态以及初始状态;
- 补:终止状态取补
- 差
- 交
- 反转:新增终止状态,原终止状态空转移到新终止状态,然后所有边逆向,是(非)终止状态改为非(是)终止状态;
证明思路
- 略
9. 上下文无关文法(CFG)
定义:上下文无关文法(CFG, 简称文法) G 是一个四元组 G = ( V , T , P , S ) G = (V, T, P, S) G=(V,T,P,S)
- V V V : 变元的有穷集, 变元也称为非终结符或语法范畴;
- T T T: 终结符的有穷集, 且 V ∩ T = ∅;
- P P P: 产生式的有穷集, 每个产生式包括:
- 一个变元, 称为“产生式的头或左部”;
- 一个产生式符号 →, 读作“定义为”;
- 一个 ( V ∪ T ) ∗ (V ∪ T)^* (V∪T)∗中的符号串, 称为“体或右部”;
- S ∈ V S ∈V S∈V:初始符号, 文法开始的地方.
产生
- 产生式 A → α A → α A→α,读作 A 定义为 α
- 如果有多个 A 的产生式 A → α 1 , A → α 2 , ⋅ ⋅ ⋅ , A → α n A → α_1, A → α_2, · · · , A → α_n A→α1,A→α2,⋅⋅⋅,A→αn
- 可简写为 A → α 1 ∣ α 2 ∣ ⋅ ⋅ ⋅ ∣ α n A → α_1 | α_2 | · · · | α_n A→α1∣α2∣⋅⋅⋅∣αn
- 文法中变元 A 的全体产生式, 称为 A 产生式
符号
- 终结符: 0, 1, . . . , a, b, . . .
- 终结符串: . . . , w, x, y, z
- 非终结符: S, A, B, . . .
- 终结符或非终结符: . . . , X, Y, Z
- 终结符或非终结符组成的串: α, β, γ, . . .
例:
- 回文
G = ( A , 0 , 1 , A → ε ∣ 0 ∣ 1 ∣ 0 A 0 ∣ 1 A 1 , A ) G = ({A}, {0, 1}, {A → ε | 0 | 1 | 0A0 | 1A1}, A) G=(A,0,1,A→ε∣0∣1∣0A0∣1A1,A)- L={ w∈{0,1}* | w contains same number of 0’s and 1’s }
R = ( S , 0 , 1 , P , S ) R = ({S }, {0,1}, P, S ) R=(S,0,1,P,S)
P : S → ε ∣ 0 S 1 ∣ 1 S 0 ∣ S S P:S → ε | 0S1 | 1S0 | SS P:S→ε∣0S1∣1S0∣SS
- 从字符串到文法变元的分析过程, 称为递归推理或归约;
归约: 自底向上, 由产生式的体向头的分析 - 从文法变元到字符串的分析过程, 称为推导或派生.
派生: 自顶向下, 由产生式的头向体分析
9.1 规约
例:用算数表达式文法 G e x p G_{exp} Gexp, 将 a ∗ ( a + b 00 ) a ∗ (a + b00) a∗(a+b00) 归约的过程
- E → I
- E → E + E
- E → E ∗ E
- E → (E)
- I → a
- I → b
- I → Ia
- I → Ib
- I → I0
- I → I1
目标:从 a ∗ ( a + b 00 ) a ∗ (a + b00) a∗(a+b00)规约到 E E E
解:
- a ∗ ( a + b 00 ) a ∗ (a + b00) a∗(a+b00)
- I ∗ ( I + b 00 ) I ∗ (I + b00) I∗(I+b00)
- I ∗ ( I + I 00 ) I ∗ (I + I00) I∗(I+I00)
- I ∗ ( I + I 0 ) I ∗ (I + I0) I∗(I+I0)
- I ∗ ( I + I ) I ∗ (I + I) I∗(I+I)
- E ∗ ( E + E ) E ∗ (E + E) E∗(E+E)
- E ∗ E E ∗ E E∗E
- E E E
9.2 派生
- 最左派生
- 最右派生
为限制派生的随意性, 要求只替换符号串中最左边变元的派生过程, 称为最
左派生, 记为
⟹ l m 或 ⟹ lm ∗ \underset{lm}{\Longrightarrow} 或 \overset{*}{\underset{\text{lm}}{\Longrightarrow}} lm⟹或lm⟹∗
只替换最右的, 称为最右派生, 记为
⟹ r m 或 ⟹ rm ∗ \underset{rm}{\Longrightarrow} 或 \overset{*}{\underset{\text{rm}}{\Longrightarrow}} rm⟹或rm⟹∗
任何派生都有等价的最左派生和最右派生
- A ⟹ ∗ w A\overset{*}{\Longrightarrow}w A⟹∗w 当且仅当 A ⟹ lm ∗ w A\overset{*}{\underset{\text{lm}}{\Longrightarrow}}w Alm⟹∗w 当且仅当 A ⟹ rm ∗ w A\overset{*}{\underset{\text{rm}}{\Longrightarrow}}w Arm⟹∗w
- 即:最左和最右派生同时存在或不存在
当 w w w在 L ( G ) L(G) L(G)中时满足:
- w w w仅由终结符组成
- 初始符号 S S S能派生出 w w w
即:
L ( G ) = { w ∣ w ϵ T ∗ , S ⟹ G ∗ w } L\left( G \right) = \left\{ w\ |\ w\epsilon T^{*},\ S\overset{*}{\underset{G}{\Longrightarrow}}w \right\} L(G)={w ∣ wϵT∗, SG⟹∗w}
语言 L 是某个 CFG G 定义的语言, 即 L = L ( G ) L = L(G) L=L(G), 则称 L 为上下文无关语言(CFL, Context-Free Language).
- 上下文无关是指在文法派生的每一步 α A β ⇒ α γ β αAβ ⇒ αγβ αAβ⇒αγβ,符号串 γ 仅根据 A 的产生式派生, 而无需依赖 A 的上下文 α 和 β.
- 如果有两个文法 CFG G1 和 CFG G2,满足L(G1) = L(G2),则称 G1 和 G2 是等价的.
- 句型
- 若 C F G G = ( V , T , P , S ) CFG G = (V, T, P, S) CFGG=(V,T,P,S), 初始符号 S 派生出来的符号串, 称为 G 的句型, 即
- α ∈ ( V ∪ T ) ∗ \alpha \in \left( V \cup T \right)^{*} α∈(V∪T)∗且 S ⟹ ∗ a S\overset{*}{\Longrightarrow}a S⟹∗a
- 如果 S ⟹ lm ∗ α S\overset{*}{\underset{\text{lm}}{\Longrightarrow}}\alpha Slm⟹∗α,称 α \alpha α为左句型
- 如果 S ⟹ rm ∗ α S\overset{*}{\underset{\text{rm}}{\Longrightarrow}}\alpha Srm⟹∗α,称 α \alpha α为右句型
- 只含有终结符的句型, 也称为 G 的句子
- 而 L(G) 就是文法 G 全部的句子
9.3 解析树
CFG G = (V, T, P, S) 的语法分析树(语法树或派生树) 为:
- 每个内节点标记为 V 中的变元符号;
- 每个叶节点标记为 V ∪ T ∪ {ε} 中的符号;
- 如果某内节点标记是 A, 其子节点从左至右分别为X1, X2, · · · , Xn
- 那么 A → X 1 X 2 ⋅ ⋅ ⋅ X n ∈ P A → X1X2 · · · Xn ∈ P A→X1X2⋅⋅⋅Xn∈P
- 若有 Xi = ε, 则 ε 是 A 唯一子节点, 且 A → ε ∈ P
- 语法树的全部叶节点从左到右连接起来, 称为该树的产物或结果. 如果树根节点是初始符号 S, 叶节点是终结符或 ε, 那么该树的产物属于 L(G).
- 语法树中标记为 A 的内节点及其全部子孙节点构成的子树, 称为 A 子树.
CFG G = (V, T, P, S) 且 A ∈ V , 那么文法 G 中
- A ⟹ ∗ α A\overset{*}{\Longrightarrow}\alpha A⟹∗α 当且仅当 G 中存在以 A 为根节点产物为 α 的语法树
- 每棵语法分析树都有唯一的最左 (右) 派生
- 给定 CFG G = (V, T, P, S), A ∈ V , 以下命题等价:
- 通过递归推理, 确定串 w 在变元 A 的语言中
- 存在以 A 为根节点, 产物为 w 的语法分析树
- A ⟹ ∗ w A\overset{*}{\Longrightarrow}w A⟹∗w
- A ⟹ lm ∗ w A\overset{*}{\underset{\text{lm}}{\Longrightarrow}}w Alm⟹∗w
- A ⟹ rm ∗ w A\overset{*}{\underset{\text{rm}}{\Longrightarrow}}w Arm⟹∗w
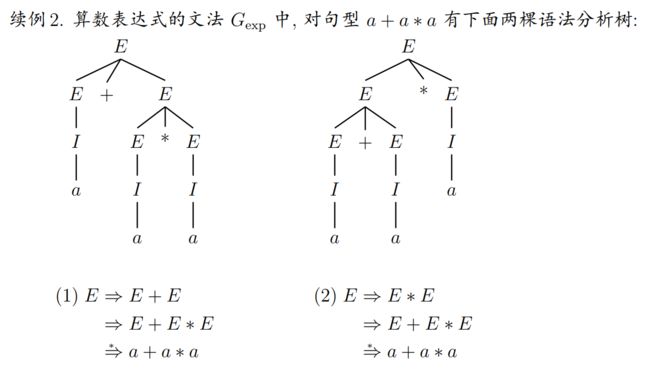
9.4 歧义
有些文法的歧义性, 可以通过重新设计文法来消除
- 定义同样的语言可以有多个文法, 如果 CFL L 的所有文法都是歧义的,那么称语言 L 是固有歧义的
- 定义同样的语言可以有多个文法, 如果 CFL L 的所有文法都是歧义的, 那么称语言 L 是固有歧义的.
- “判定任何给定 CFG G 是否歧义”是一个不可判定问题
10. 上下文无关文法的化简
文法化简的可靠顺序
- 消除ε-产生式;
- 消除单元产生式;
- 消除非产生的无用符号;
- 消除非可达的无用符号.
10.1 消除无用符号
- 无用符号:对文法定义语言没有贡献的符号
- 初始符号在派生过程中能派生的语言,前后为若干终止符、中间的单一符号为可达的;
- 某一符号和前后的若干终止符能够最终派生为均为终止符的语言,则其是产生的;
- 可达 + 产生 = 有用
- 非(有用)= 无用 = 非(可达) 或 非(产生)
步骤:
- 计算“产生的”符号集
- 每个 T 中的符号都是产生的
- A → α ∈ P 且 α 中符号都是产生的, 则 A 是产生的
- 计算“可达的”符号集
- 符号 S 是可达的
- A → α ∈ P 且 A 是可达的, 则 α 中符号都是可达的
- 删除全部含有 “非产生的” 和 “非可达的” 符号的产生式
注:先寻找并消除全部非“产生的”符号,再寻找并消除全部非“可达的”符号,否则可能消除不完整。
- 例:消除如下文法无用符号
S → AB | a
A → b - 解:S → bB | a
10.2 消除ε产生式
步骤:
- 确定“可空变元”
- 如果 A → ε, 则 A 是可空的
- 如果 B → α 且 α 中的每个符号都是可空的,则 B 是可空的
- 确定“可空变元”
- 将含有可空变元的一条产生式 A → X 1 X 2 ⋅ ⋅ ⋅ X n A → X_1X_2 · · · X_n A→X1X2⋅⋅⋅Xn用一组产生式 A → Y 1 Y 2 ⋅ ⋅ ⋅ Y n A → Y_1Y_2 · · · Y_n A→Y1Y2⋅⋅⋅Yn代替,其中
- 若 Xi 不是可空的, Yi 为 Xi
- 若 Xi 是可空的, Yi 为 Xi 或 ε
- 但 Yi 不能全为 ε (否则A为可空变元)
- 将含有可空变元的一条产生式 A → X 1 X 2 ⋅ ⋅ ⋅ X n A → X_1X_2 · · · X_n A→X1X2⋅⋅⋅Xn用一组产生式 A → Y 1 Y 2 ⋅ ⋅ ⋅ Y n A → Y_1Y_2 · · · Y_n A→Y1Y2⋅⋅⋅Yn代替,其中
例:
- 消除 CFG G = ({S, A, B}, {a, b}, P, S) 的 ε-产生式.
S → AB
A → AaA | ε
B → BbB | ε解:
- CFG G′ 为
S → AB | A | B
A → AaA | Aa | aA | a
B → BbB | Bb | bB | b
10.3 消除单元产生式
单元产生式:例如 A → B
步骤:
- 确定“单元对”
- 如果有 A ⟹ ∗ B A\overset{*}{\Longrightarrow}B A⟹∗B, 则称 [ A , B ] [A, B] [A,B] 为单元对
- A → B ∈ P, 则 [A, B] 是单元对
- 若 [A, B] 和 [B, C] 都是单元对, 则 [A, C] 是单元对
- 消除单元产生式
- 删除全部形为 A → B 的单元产生式
- 对每个单元对 [A, B], 将 B 的产生式复制给 A
例:
- 消除文法的单元产生式
S → A | B | 0S1
A → 0A | 0
B → 1B | 1解:
- 单位对为 [S, A] 和 [S, B], 带入得:
S → 0S1
S → 0A | 0
S → 1B | 1
A → 0A | 0
B → 1B | 1
11. 上下文无关文法的范式
11.1 乔姆斯基范式(CNF)
- 每个不带 ε 的 CFL 都可以由这样的 CFG G 定义, G 中每个产生式的形式都为 A → B C A → BC A→BC 或 A → a A → a A→a
- 这里的 A, B 和 C 是变元, a 是终结符.
- 利用 CNF 派生长度为 n 的串, 刚好需要 2n − 1 步
例:
- CFG G = ( S , A , B , a , b , P , S ) G = ({S, A, B}, {a, b}, P, S) G=(S,A,B,a,b,P,S), 产生式集合 P 为:
S → b A ∣ a B S → bA | aB S→bA∣aB
A → b A A ∣ a S ∣ a A → bAA | aS | a A→bAA∣aS∣a
B → a B B ∣ b S ∣ b B → aBB | bS | b B→aBB∣bS∣b- 请设计等价的 CNF 文法.
解:
- CNF 为:
S → C b A ∣ C a B S → CbA | CaB S→CbA∣CaB
A → C a S ∣ C b D 1 ∣ a A → C_aS | C_bD_1 | a A→CaS∣CbD1∣a
D 1 → A A D1 → AA D1→AA
C a → a C_a → a Ca→a
B → C b S ∣ C a D 2 ∣ b B → C_bS | C_aD_2 | b B→CbS∣CaD2∣b
D 2 → B B D2 → BB D2→BB
C b → b C_b → b Cb→b
11.2 格雷巴赫范式(GNF)
- 每个不带 ε 的 CFL 都可以由这样的 CFG G 定义, G 中每个产生式的形式都为 A → a α A → aα A→aα
其中 A 是变元, a 是终结符, α 是零或多个变元的串.
- GNF 每个产生式都会引入一个终结符
- 长度为 n 的串的派生恰好是 n 步
例:
- 将以下文法转换为 GNF.
S → AB
A → aA | bB | b
B → b
解:
- GNF 为
S → aAB | bBB | bB
A → aA | bB | b
B → b
特殊情况:
- 直接左递归
- 间接左递归
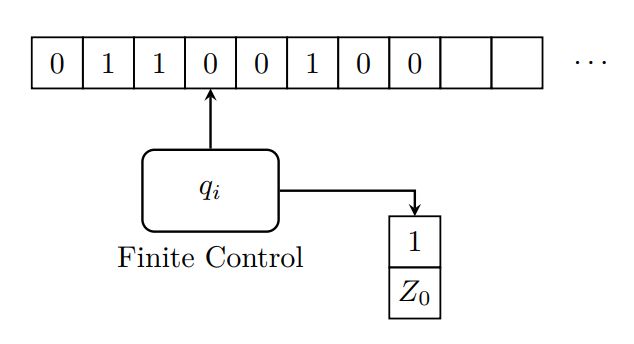
12. 下推自动机(PDA)
下推自动机(PDA, Pushdown Automata) P 为七元组
P = ( Q , Σ , Γ , δ , q 0 , Z 0 , F ) P = (Q, Σ, Γ, δ, q_0, Z_0, F) P=(Q,Σ,Γ,δ,q0,Z0,F)
- Q Q Q, 有穷状态集;
- Σ Σ Σ, 有穷输入符号集;
- Γ Γ Γ, 有穷栈符号集;
- δ : Q × ( Σ ∪ ε ) × Γ → 2 Q × Γ ∗ δ : Q × (Σ ∪ {ε}) × Γ → 2^{Q×Γ^∗} δ:Q×(Σ∪ε)×Γ→2Q×Γ∗, 状态转移函数;
- q 0 ∈ Q q0 ∈ Q q0∈Q, 初始状态;
- Z 0 ∈ Γ − Σ Z_0 ∈ Γ − Σ Z0∈Γ−Σ, 栈底符号;
- F ⊆ Q F ⊆ Q F⊆Q, 接收状态集或终态集.
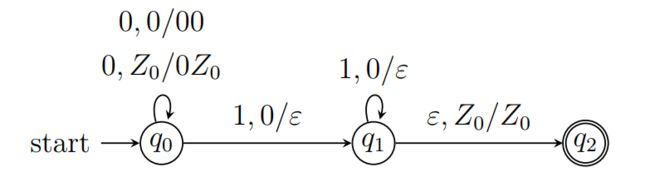
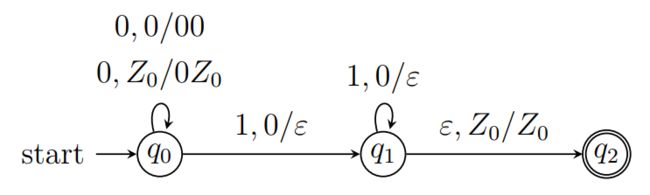
例:设计识别 L 01 = { 0 n 1 n ∣ n ≥ 1 } L_{01} = \{0^n1^n | n ≥ 1\} L01={0n1n∣n≥1} 的 PDA
例:设计识别 L w w r = { w w R ∣ w ∈ ( 0 + 1 ) ∗ } L_{ww^r} = \{ww^R | w ∈ (0 + 1)^∗\} Lwwr={wwR∣w∈(0+1)∗} 的 PDA
12.1 瞬时描述(ID)
为描述 PDA 瞬间的格局, 定义 Q × Σ ∗ × Γ ∗ Q × Σ^∗ × Γ^∗ Q×Σ∗×Γ∗ 中三元组
( q , w , γ ) (q, w, γ) (q,w,γ)
为瞬时描述(ID, Instantaneous Description), 表示此时 PDA 处于状态 q q q, 剩
余输入串 w w w, 栈为 γ γ γ.
12.1.1 转移
在 PDA P P P 中如果 ( p , β ) ∈ δ ( q , a , Z ) (p, β) ∈ δ(q, a, Z) (p,β)∈δ(q,a,Z), 由 ( q , a w , Z α ) (q, aw, Zα) (q,aw,Zα) 到 ( p , w , β α ) (p, w, βα) (p,w,βα) 的变化, 称为瞬时描述(ID)的转移 ⊢ P ⊢_P ⊢P, 记为
( q , a w , Z α ) ⊢ P ( p , w , β α ) (q, aw, Zα) ⊢_P (p, w, βα) (q,aw,Zα)⊢P(p,w,βα)
其中 w ∈ Σ ∗ , α ∈ Γ ∗ w ∈ Σ^∗, α ∈ Γ^∗ w∈Σ∗,α∈Γ∗.
若有瞬时描述(ID) I I I, J J J 和 K K K, 递归定义 ⊢ P ∗ ⊢^*_P ⊢P∗ 为:
- I ⊢ P ∗ I I ⊢^*_P I I⊢P∗I
- 若 I ⊢ P ∗ J I ⊢^*_P J I⊢P∗J, J ⊢ P ∗ K J ⊢^*_P K J⊢P∗K,则 I ⊢ P ∗ K I ⊢^*_P K I⊢P∗K
若 P P P 已知, 可省略, 记为 ⊢ ⊢ ⊢ 和 ⊢ ∗ ⊢^* ⊢∗ .
例:语言 L 01 = { 0 n 1 n ∣ n ≥ 1 } L_{01} = \{0^n1^n | n ≥ 1\} L01={0n1n∣n≥1} 的 PDA, 识别 0011 时的 ID 序列.
解:
( q 0 , 0011 , Z 0 ) ⊢ ( q 0 , 011 , 0 Z 0 ) ⊢ ( q 0 , 11 , 00 Z 0 ) ⊢ ( q 1 , 1 , 0 Z 0 ) ⊢ ( q 1 , ε , Z 0 ) ⊢ ( q 2 , ε , Z 0 ) (q_0, 0011, Z_0) ⊢ (q_0, 011, 0Z_0) ⊢ (q_0, 11, 00Z_0) ⊢ (q_1, 1, 0Z_0) ⊢ (q_1, ε, Z_0) ⊢ (q_2, ε, Z_0) (q0,0011,Z0)⊢(q0,011,0Z0)⊢(q0,11,00Z0)⊢(q1,1,0Z0)⊢(q1,ε,Z0)⊢(q2,ε,Z0)
定理:
-
对 ∀ w ∈ Σ ∗ , ∀ γ ∈ Γ ∗ ∀w ∈ Σ^∗, ∀γ ∈ Γ^∗ ∀w∈Σ∗,∀γ∈Γ∗, 如果
( q , x , α ) ⊢ P ∗ ( p , y , β ) , (q, x, α) ⊢^*_P (p, y, β), (q,x,α)⊢P∗(p,y,β),
那么
( q , x w , α γ ) ⊢ P ∗ ( p , y w , β γ ) (q, xw, αγ) ⊢^*_P (p, yw, βγ) (q,xw,αγ)⊢P∗(p,yw,βγ)
即:在可以转移的两个瞬时描述的剩余输入串后加入相同的剩余输入串、栈后加入相同的栈,仍然可以转移; -
对 ∀ w ∈ Σ ∗ ∀w ∈ Σ^∗ ∀w∈Σ∗, 如果
( q , x w , α ) ⊢ P ∗ ( p , y w , β ) , (q, xw, α) ⊢^*_P (p, yw, β), (q,xw,α)⊢P∗(p,yw,β),
那么
( q , x , α ) ⊢ P ∗ ( p , y , β ) (q, x, α) ⊢^*_P (p, y, β) (q,x,α)⊢P∗(p,y,β)
即:在可以转移的两个瞬时描述的剩余输入串后删除相同的输入串,仍然可以转移;
12.2 下推自动机接受的语言(终态/空栈)
PDA P = ( Q , Σ , Γ , δ , q 0 , Z 0 , F ) P = (Q, Σ, Γ, δ, q_0, Z_0, F) P=(Q,Σ,Γ,δ,q0,Z0,F), 以两种方式接受语言:
- P 以终态方式接受的语言, 记为 L ( P ) L(P) L(P), 定义为 L ( P ) = w ∣ ( q 0 , w , Z 0 ) ⊢ ∗ ( p , ε , γ ) , p ∈ F . L(P) = {w | (q_0, w, Z_0) ⊢^*(p, ε, γ), p ∈ F}. L(P)=w∣(q0,w,Z0)⊢∗(p,ε,γ),p∈F.
- P 以空栈方式接受的语言, 记为 N ( P ) N(P) N(P), 定义为 N ( P ) = w ∣ ( q 0 , w , Z 0 ) ⊢ ∗ ( p , ε , ε ) . N(P) = {w | (q_0, w, Z_0) ⊢^*(p, ε, ε)}. N(P)=w∣(q0,w,Z0)⊢∗(p,ε,ε).
定理及证明(构造)方法:
- 如果 PDA P F P_F PF 以终态方式接受语言 L,那么一定存在 PDA P N P_N PN 以空栈方式接受 L: P F = ( Q , Σ , Γ , δ F , q 0 , Z 0 , F ) P_F = (Q, Σ, Γ, δ_F, q_0, Z_0, F) PF=(Q,Σ,Γ,δF,q0,Z0,F) 构造 P N = ( Q ∪ { p 0 , p } , Σ , Γ ∪ { X 0 } , δ N , p 0 , X 0 , ∅ ) P_N = (Q ∪ \{p_0, p\}, Σ, Γ ∪ \{X0\}, δ_N, p_0, X_0, ∅) PN=(Q∪{p0,p},Σ,Γ∪{X0},δN,p0,X0,∅)
终止状态时,空转移到 p p p、弹栈栈底符号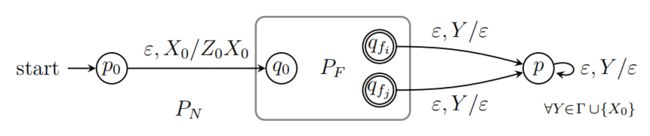
- 反之亦然: P N = ( Q , Σ , Γ , δ N , q 0 , Z 0 , ∅ ) P_N = (Q, Σ, Γ, δ_N, q_0, Z_0, ∅) PN=(Q,Σ,Γ,δN,q0,Z0,∅) 构造 P F = ( Q ∪ { p 0 , p f } , Σ , Γ ∪ { X 0 } , δ F , p 0 , X 0 , { p f } ) P_F = (Q ∪ \{p_0, p_f\}, Σ, Γ ∪ \{X_0\}, δ_F, p_0, X_0, \{p_f\}) PF=(Q∪{p0,pf},Σ,Γ∪{X0},δF,p0,X0,{pf})
空栈时,空转移到新建的终止状态 p f p_f pf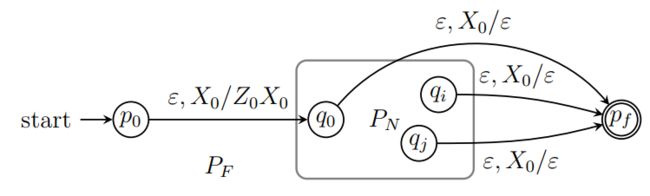
例1:识别 L w w r L_{ww^r} Lwwr 的 PDA P P P , 从终态方式接受, 改为空栈方式接受.
- 解:
用 δ ( q 1 , ε , Z 0 ) = { ( q 1 , ε ) } δ(q_1, ε, Z_0) = \{(q_1, ε)\} δ(q1,ε,Z0)={(q1,ε)} 代替 δ ( q 1 , ε , Z 0 ) = { ( q 2 , Z 0 ) } δ(q_1, ε, Z_0) = \{(q_2, Z_0)\} δ(q1,ε,Z0)={(q2,Z0)} 即可

例2:接受 L = { w ∈ { 0 , 1 } ∗ ∣ w 中 字 符 0 和 1 的 数 量 相 同 } L = \{w ∈ \{0, 1\}^∗ | w 中字符 0 和 1 的数量相同\} L={w∈{0,1}∗∣w中字符0和1的数量相同} 的 PDA
- 栈空时,压栈;
- 栈不空时:
- 若输入符与栈顶相同,压栈;
- 若输入符与栈顶不同,弹栈;
- 栈空为接受状态。
例3:接受 L = { 0 n 1 m ∣ 0 ≤ n ≤ m ≤ 2 n } L = \{0^n1^m | 0 ≤ n ≤ m ≤ 2n\} L={0n1m∣0≤n≤m≤2n} 的 PDA
- 定义:左、中、右、下4个状态
- 左状态:读入0(自身递归转移)
- 转移到中状态:空转移(栈中有0或无0都可)
- 中状态:读入1
- 转移到下状态:(栈中有至少一个0,至少连续2个1)读入一个1,不弹栈
- 下状态转移回来:再读入一个1,弹栈
- 和下状态的一个来回读入2个1
- 自身转移:当1的个数是奇数
- 右状态:空栈,结束
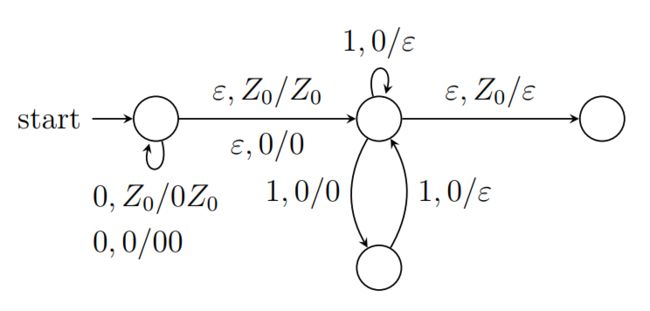
13. CFG ⟺ \Longleftrightarrow ⟺PDA(等价性)
13.1 CFG ⟹ \Longrightarrow ⟹PDA
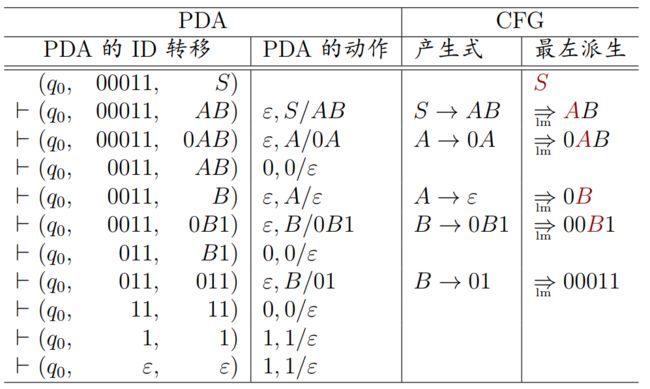
例:设计语言 L = { 0 n 1 m ∣ 1 ≤ m ≤ n } L = \{0^n1^m | 1 ≤ m ≤ n\} L={0n1m∣1≤m≤n} 的 PDA,并转换为CFG
解:
-
CFG G:
S → A B S → AB S→AB
A → 0 A ∣ ε A → 0A | ε A→0A∣ε
B → 0 B 1 ∣ 01 B → 0B1 | 01 B→0B1∣01 -
字符串 00011 的最左派生:
S ⟹ l m A B ⟹ l m 0 A B ⟹ l m 0 B ⟹ l m 00 B 1 ⟹ l m 00011 S \underset{lm}{\Longrightarrow} AB \underset{lm}{\Longrightarrow} 0AB \underset{lm}{\Longrightarrow} 0B \underset{lm}{\Longrightarrow} 00B1 \underset{lm}{\Longrightarrow} 00011 Slm⟹ABlm⟹0ABlm⟹0Blm⟹00B1lm⟹00011
用 PDA 栈顶符号的替换, 模拟文法的最左派生
- 栈顶为变元:输入 ε ε ε,变元派生(如: ε , S → 0 S 1 ε, S → 0S1 ε,S→0S1)
- 栈顶为终结符:输入非空字符,输入串减少,栈顶弹出
13.2 PDA ⟹ \Longrightarrow ⟹CFG
如果 PDA P = ( Q , Σ , Γ , δ , q 0 , Z 0 , ∅ ) P = (Q, Σ, Γ, δ, q_0, Z_0, ∅) P=(Q,Σ,Γ,δ,q0,Z0,∅), 那么构造 CFG G = ( V , Σ , P ′ , S ) G = (V, Σ, P^′, S) G=(V,Σ,P′,S), 其中
V V V 和 P ′ P^′ P′ 为
- V = { [ q X p ] ∣ p , q ∈ Q , X ∈ Γ } ∪ { S } V = \{[qXp] | p,q ∈Q, X ∈ Γ\} ∪ \{S\} V={[qXp]∣p,q∈Q,X∈Γ}∪{S};
- 对 ∀ p ∈ Q ∀p ∈ Q ∀p∈Q, 构造产生式 S → [ q 0 Z 0 p ] S → [q_0Z_0p] S→[q0Z0p];
- 对 ∀ ( p , Y 1 Y 2 ⋅ ⋅ ⋅ Y n ) ∈ δ ( q , a , X ) ∀(p, Y_1Y_2 · · · Y_n) ∈ δ(q, a, X) ∀(p,Y1Y2⋅⋅⋅Yn)∈δ(q,a,X), 构造 ∣ Q ∣ n |Q|n ∣Q∣n 个产生式
[ q X r n ] → a [ p Y 1 r 1 ] [ r 1 Y 2 r 2 ] ⋅ ⋅ ⋅ [ r n − 1 Y n r n ] [qXr_n] → a[pY_1r_1][r_1Y_2r_2] · · · [r_{n−1}Y_nr_n] [qXrn]→a[pY1r1][r1Y2r2]⋅⋅⋅[rn−1Ynrn]
其中 a ∈ Σ ∪ { ε } a ∈ Σ ∪ \{ε\} a∈Σ∪{ε}, X , Y i ∈ Γ X,Y_i ∈ Γ X,Yi∈Γ, 而 r i ∈ Q r_i ∈ Q ri∈Q 是 n n n 次 ∣ Q ∣ |Q| ∣Q∣ 种状态的组合; 若 i = 0 i = 0 i=0, 为 [ q X p ] → a [qXp] → a [qXp]→a.
例:将 PDA P = ({p, q}, (0, 1), {X, Z}, δ, q, Z) 转为 CFG, 其中 δ 如下:
14. GNF ⟹ \Longrightarrow ⟹PDA
如果 GNF 格式的 CFG G = ( V , T , P ′ , S ) G = (V, T, P^′, S) G=(V,T,P′,S), 那么构造 PDA
P = ( { q } , T , V , δ , q , S , ∅ ) P = (\{q\}, T, V, δ, q, S, ∅) P=({q},T,V,δ,q,S,∅)
为每个产生式, 定义 δ 为:
δ ( q , a , A ) = { ( q , β ) ∣ A → a β ∈ P ′ } δ(q, a, A) = \{(q, β) | A → aβ ∈ P^′\} δ(q,a,A)={(q,β)∣A→aβ∈P′}
即:每次读入终结符,将栈中变元进行派生(弹栈+压栈),直到栈中均为终结符。
例:文法 S → a A A , A → a S ∣ b S ∣ a S → aAA, A → aS | bS | a S→aAA,A→aS∣bS∣a 为 GNF 格式, 构造等价的 PDA
15. 确定性下推自动机(DPDA)
如果 PDA P = ( Q , Σ , Γ , δ , q 0 , Z 0 , F ) P = (Q, Σ, Γ, δ, q_0, Z_0, F) P=(Q,Σ,Γ,δ,q0,Z0,F) 满足
- ∀ a ∈ Σ ∪ { ε } ∀a ∈ Σ ∪ \{ε\} ∀a∈Σ∪{ε}, δ ( q , a , X ) δ(q, a, X) δ(q,a,X) 至多有一个动作;
- ∀ a ∈ Σ ∀a ∈ Σ ∀a∈Σ, 如果 δ ( q , a , X ) ≠ ∅ δ(q, a, X) \neq ∅ δ(q,a,X)=∅, 那么 δ ( q , ε , X ) = ∅ . δ(q, ε, X) = ∅. δ(q,ε,X)=∅.
∀ ( q , a , Z ) ∈ Q × Σ × Γ ∀(q, a, Z) ∈ Q × Σ × Γ ∀(q,a,Z)∈Q×Σ×Γ 满足 ∣ δ ( q , a , Z ) ∣ + ∣ δ ( q , ε , Z ) ∣ ≤ 1 |δ(q, a, Z)| + |δ(q, ε, Z)| ≤ 1 ∣δ(q,a,Z)∣+∣δ(q,ε,Z)∣≤1
即:每一个瞬时描述下至多有一个转移状态(可以无动作)
则称 P P P 为确定型下推自动机(DPDA)
-
DPDA P P P 以终态方式接受的语言 L ( P ) L(P) L(P) 称为确定性上下文无关语言(DCFL)
-
注:DPDA 与 PDA 不等价
例:任何 DPDA 都无法接受 L w w r L_{ww^r} Lwwr, 但是可以接受
L w c w r = { w c w R ∣ w ∈ ( 0 + 1 ) ∗ } L_{wcw^r} = \{wcw^R | w ∈ (0 + 1)^∗\} Lwcwr={wcwR∣w∈(0+1)∗}
设计DPDA
DCFL 的重要应用
- 非固有歧义语言的真子集
- 程序设计语言的语法分析器
- LR(k) 文法, Yacc 的基础, 解析时间复杂度为 O(n)
- 如果 L L L 是正则语言, 那么存在 DPDA P P P 以终态方式接受 L L L, 即 L = L ( P ) L = L(P) L=L(P)
- 证明: 显然,DPDA P P P 可以不用栈而模拟任何 DFA。
- 结论: 正 则 语 言 ⊆ D C F L ⊆ C F L 正则语言 ⊆ DCFL ⊆ CFL 正则语言⊆DCFL⊆CFL
- 前缀性质:如果语言 L 中不存在字符串 x 和 y, 使 x 是 y 的前缀, 称语言 L 满足前缀性质.
- DPDA P P P 且 L = N ( P ) L = N(P) L=N(P), 当且仅当 L L L 有前缀性质, 且存在 DPDA P ′ P^′ P′ 使 L = L ( P ′ ) L = L(P ′) L=L(P′).
- DPDA P P P 的 N ( P ) N(P) N(P) 更有限, 即使正则语言 0 ∗ 0^∗ 0∗ 也无法接受
- 但却可以被某个 DPDA 以终态方式接受
DPDA 与歧义文法
DPDA P P P, 语言 L = L ( P ) L = L(P) L=L(P), 那么 L L L 有无歧义的 CFG
- 因此 DPDA 在语法分析中占重要地位
- 但是并非所有非固有歧义 CFL 都会被 DPDA 识别
如 L w w r L_{ww^r} Lwwr有无歧义文法 S → 0 S 0 ∣ 1 S 1 ∣ ε S → 0S0 | 1S1 | ε S→0S0∣1S1∣ε
16 上下文无关语言的泵引理
如果语言 L L L 是 CFL, 那么存在正整数 N N N, 对 ∀ z ∈ L ∀z ∈ L ∀z∈L,
只要 ∣ z ∣ ≥ N |z| ≥ N ∣z∣≥N, 就可以将 z z z 分为五部分 z = u v w x y z = uvwxy z=uvwxy 满足:
- v x ≠ ε vx \neq ε vx=ε (或 ∣ v x ∣ > 0 |vx| > 0 ∣vx∣>0);
- ∣ v w x ∣ ≤ N |vwx| ≤ N ∣vwx∣≤N;
- ∀ i ≥ 0 , u v i w x i y ∈ L ∀i ≥ 0, uv^iwx^iy ∈ L ∀i≥0,uviwxiy∈L.
例:证明 L = { 0 n 1 n 2 n ∣ n ≥ 1 } L = \{0^{n}1^{n}2^{n} | n ≥ 1\} L={0n1n2n∣n≥1} 不是上下文无关语言
解:
- 假设 L L L 是 CFL, 那么存在整数 N, 对 ∀ z ∈ L ( ∣ z ∣ ≥ N ) ∀z ∈ L (|z| ≥ N) ∀z∈L(∣z∣≥N) 满足泵引理.
- 从 L L L 中取 z = 0 N 1 N 2 N z = 0N1N2N z=0N1N2N, 则显然 z ∈ L z ∈ L z∈L 且 ∣ z ∣ = 3 N ≥ N |z| = 3N ≥ N ∣z∣=3N≥N.
- 由泵引理, z z z 可被分为 z = u v w x y z = uvwxy z=uvwxy, 且有 ∣ v w x ∣ ≤ N |vwx| ≤ N ∣vwx∣≤N 和 v x ≠ ε vx \neq ε vx=ε.
- 那么 v w x vwx vwx 可能
- 只包含 0, 1 或 2, 那么 u w y ∉ L uwy \notin L uwy∈/L;
- 只包含 0 和 1, 或只包含 1 和 2, 那么也有 u w y ∉ L uwy \notin L uwy∈/L;
- 与泵引理 u w y = u v 0 w x 0 y ∈ L uwy = uv_0wx_0y ∈ L uwy=uv0wx0y∈L 矛盾, 假设不成立.
- L L L 不是上下文无关的
例:证明 L = { w w ∣ w ∈ 0 , 1 ∗ } L = \{ww | w ∈ {0, 1}^∗\} L={ww∣w∈0,1∗} 不是上下文无关的
(错误的) 证明: 假设 L L L 是 CFL. 取 z = 0 N 1 0 N 1 z = 0^N10^N1 z=0N10N1, 那么 z = u v w x y z = uvwxy z=uvwxy 为
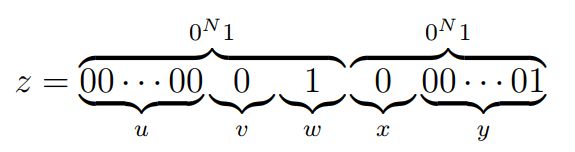
则对任意 i ≥ 0 i ≥ 0 i≥0, 有 u v i w x i y ∈ L uv^iwx^iy ∈ L uviwxiy∈L, 满足泵引理.
(正确的) 证明: 假设 L L L 是 CFL. 取 z = 0 N 1 N 0 N 1 N z = 0^N1^N0^N1^N z=0N1N0N1N, 将 z z z 分为 z = u v w x y z = uvwxy z=uvwxy 时
- 若 v w x vwx vwx 在 z z z 中点的一侧, u v 0 w x 0 y uv_0wx_0y uv0wx0y 显然不可能属于 L L L;
- 若 v w x vwx vwx 包括 z z z 中点, 那么 u v 0 w x 0 y uv_0wx_0y uv0wx0y 为 0 N 1 i 0 j 1 N 0^N1^i0^j1^N 0N1i0j1N, 也不可能属于 L L L.
所以假设不成立, L L L 不是 CFL
17 上下文无关语言的封闭性
封闭
- 并
- 连接
- 闭包
- 同态
- 逆同态
- 反转
不封闭
- 交
- 补运算
17.1 代换
两个字母表 Σ \Sigma Σ 到 Γ \Gamma Γ 的函数 s : Σ → 2 Γ ∗ s\ :\ \Sigma\ \rightarrow 2^{\Gamma^{*}} s : Σ →2Γ∗ 称为代换. Σ \Sigma Σ 中的一个字符 a a a 在 s s s 的作用下为
Γ \Gamma Γ 上的一个语言 L a L_{a} La, 即
s ( a ) = L a s(a)\ = \ La s(a) = La
扩展 s s s 的定义到字符串,
s ( ε ) = ε s(\varepsilon)\ = \ \varepsilon s(ε) = ε
s ( x a ) = s ( x ) s ( a ) s(xa)\ = \ s(x)s(a) s(xa) = s(x)s(a)
再扩展 h h h 到语言, 对 ∀ L ⊆ Σ ∗ \forall\text{L\ } \subseteq \ \Sigma^{*} ∀L ⊆ Σ∗
s ( L ) = ⋃ x ∈ L s ( x ) s(L)\ = \ \bigcup_{x \in L}^{}{s(x)} s(L) = x∈L⋃s(x)
定理:如果有 Σ Σ Σ 上的 CFL L L L 和代换 s s s, 且每个 a ∈ Σ a ∈ Σ a∈Σ 的 s ( a ) s(a) s(a) 都是 CFL, 那么 s ( L ) s(L) s(L) 也是 CFL
即:可以把CFL的每个终结符扩展为一个CFL,生成的语言还是CFL
具体构造方法:
设 CFL L L L 的文法 G = ( V , T , P , S ) G\ = \ (V,\ T,\ P,\ S) G = (V, T, P, S), 每个 s ( a ) s(a) s(a) 的文法 G a = ( V a , T a , P a , S a ) G_{a} = \ (V_{a},\ T_{a},\ P_{a},\ S_{a}) Ga= (Va, Ta, Pa, Sa).
那么 s ( L ) s(L) s(L) 的文法可以构造为
G ′ = ( V ′ , T ′ , P ′ , S ) G'\ = \ (V\ ',\ T\ ',\ P\ ',\ S)\ G′ = (V ′, T ′, P ′, S)
-
V ′ = V ∪ ( ⋃ a ∈ T V a ) V^{'}=V \cup (\bigcup_{a \in T}^{}V_{a}\ ) V′=V∪(⋃a∈TVa )
-
T ′ = ⋃ a ∈ T T a T^{'}=\bigcup_{a \in T}^{}T_{a} T′=⋃a∈TTa
-
P ′ P^{'} P′包括每个 P a P_{a} Pa 和 P P P 中产生式,但是要将 P P P的产生式中每个终结符 a a a均替换为文法 G a G_{a} Ga 的开始符号 S a S_{a} Sa.
17.2 封闭性应用
例: 请证明语言 L L L 不是 CFL L = { w ∈ { a , b , c } ∗ ∣ n a ( w ) = n b ( w ) = n c ( w ) } L = \{w ∈ {\{a, b, c\}}^∗ | n_a(w) = n_b(w) = n_c(w)\} L={w∈{a,b,c}∗∣na(w)=nb(w)=nc(w)},其中 n a ( w ) n_a(w) na(w) 表示 w w w 中 a a a 的个数.
证明:
- 因为 a ∗ b ∗ c ∗ a^∗b^∗c^∗ a∗b∗c∗ 是正则语言,
- 而 L ∩ a ∗ b ∗ c ∗ = { a n b n c n ∣ n ≥ 0 } L ∩ a^∗b^∗c^∗ = \{a^nb^nc^n | n ≥ 0\} L∩a∗b∗c∗={anbncn∣n≥0} 不是 CFL,
- 由 CFL 与正则语言的交还是 CFL, 所以 L L L 不可能是 CFL
18 上下文无关语言的判定性质
18.1 可判定的 CFL 问题
空性: 只需判断文法的开始符号 S 是否为非产生的
有穷性和无穷性:
- 用不带无用符号的 CNF 的产生式画有向图;
- 变元为顶点, 若有 A → BC, 则 A 到 B 和 C 各画一条有向边;
- 检查图中是否有循环.
成员性: 利用 CNF 范式, 有CYK算法检查串 w 是否属于 L
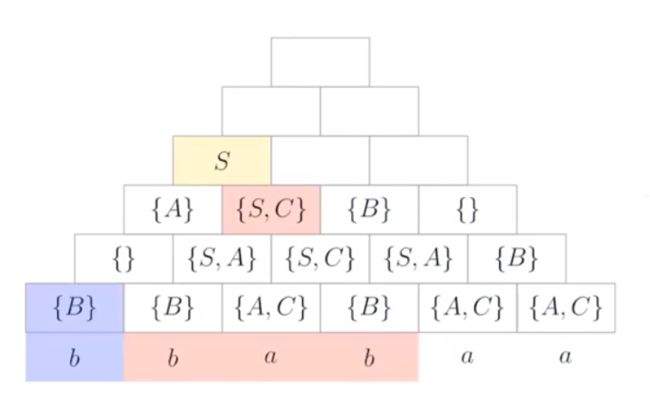
18.2 CYK算法
例:CNF G G G 如下, 用 CYK 算法判断 b b a b a a ∈ L ( G ) bbabaa ∈ L(G) bbabaa∈L(G)?
解:
S → A B ∣ B C S → AB | BC S→AB∣BC
A → B A ∣ a A → BA | a A→BA∣a
B → C C ∣ b B → CC | b B→CC∣b
C → A B ∣ a C → AB | a C→AB∣a
-
因为 S ∈ X 16 = { S , A } S ∈ X_{16} = \{S, A\} S∈X16={S,A}, 所以 b b a b a a ∈ L ( G ) bbabaa ∈ L(G) bbabaa∈L(G)
18.3 不可判定的 CFL 问题
- 判断 CFG G G G 是否歧义的?
- 判断 CFL 是否固有歧义的?
- 两个 CFL 的交是否为空?
- 两个 CFL 是否相同?
- 判断 CFL 的补是否为空? 尽管有算法判断 CFL 是否为空
- 判断 CFL 是否等于 Σ ∗ Σ^∗ Σ∗?
19. 图灵机
- 图灵机(TM, Turing Machine) M M M 为七元组
M = ( Q , Σ , Γ , δ , q 0 , B , F ) M = (Q,\Sigma,\Gamma,\delta,q_0,B,F) M=(Q,Σ,Γ,δ,q0,B,F)
- Q Q Q: 有穷状态集;
- Σ Σ Σ: 有穷输入符号集;
- Γ Γ Γ: 有穷带符号集, 且总有 Σ ⊂ Γ Σ ⊂ Γ Σ⊂Γ;
- δ : Q × Γ → Q × Γ × { L , R } δ: Q × Γ → Q × Γ × \{L, R\} δ:Q×Γ→Q×Γ×{L,R} 转移函数;
- q 0 ∈ Q q_0 ∈ Q q0∈Q: 初始状态;
- B ∈ Γ − Σ B ∈ Γ − Σ B∈Γ−Σ: 空格符号;
- F ⊆ Q F ⊆ Q F⊆Q: 终态集或接受状态集.
与有穷自动机区别:
- 可修改(必须修改,但可以相同)
- 可向左或向右移动输入带
- 有空格符号
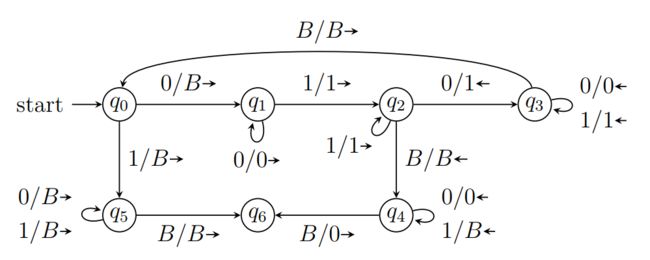
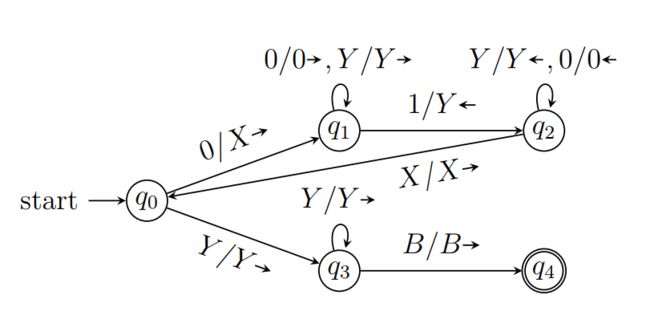
例:设计识别 { 0 n 1 n ∣ n ≥ 1 } \{0^n1^n | n ≥ 1\} {0n1n∣n≥1} 的图灵机
解:
- 每次标记一个0和一个1
- 标记0为X(X=“0已标记”)之后,越过所有未标记的0和已标记的1,将1标记为Y(Y=“1已标记”)
- 无未标记1后向右找到空格B,结束
M = ( { q 0 , q 1 , q 2 , q 3 , q 4 } , { 0 , 1 } , { 0 , 1 , X , Y , B } , δ , q 0 , B , { q 4 } ) M = (\{q0, q1, q2, q3, q4\}, \{0, 1\}, \{0, 1, X, Y, B\}, δ, q_0, B, \{q4\}) M=({q0,q1,q2,q3,q4},{0,1},{0,1,X,Y,B},δ,q0,B,{q4})

19.1 瞬时描述(ID)
图灵机虽有无穷长的带, 但经过有限步, 带上非空内容总是有限的. 因此用全部非空符号、当前状态及带头位置, 定义图灵机的瞬时描述(ID)为
X 1 X 2 ⋅ ⋅ ⋅ X i − 1 q X i X i + 1 ⋅ ⋅ ⋅ X n X_1X_2 · · · X_{i−1}qX_iX_{i+1} · · · X_n X1X2⋅⋅⋅Xi−1qXiXi+1⋅⋅⋅Xn
- 图灵机的当前状态 q q q
- 带头在左起第 i i i 个非空格符 X i X_i Xi 上
- X 1 X 2 ⋅ ⋅ ⋅ X n X_1X_2 · · · X_n X1X2⋅⋅⋅Xn是最左到最右非空格内容
如果 δ ( q , X i ) = ( p , Y , L ) δ(q, Xi) = (p, Y, L) δ(q,Xi)=(p,Y,L), 定义 ID 转移为
X 1 ⋅ ⋅ ⋅ X i − 1 q X i ⋅ ⋅ ⋅ X n ⊢ X 1 ⋅ ⋅ ⋅ X i − 2 p X i − 1 Y X i + 1 ⋅ ⋅ ⋅ X n X_1 · · · X_{i−1}qX_i · · · X_n ⊢ X_1 · · · X_{i−2}pX_{i−1}YX_{i+1} · · · X_n X1⋅⋅⋅Xi−1qXi⋅⋅⋅Xn⊢X1⋅⋅⋅Xi−2pXi−1YXi+1⋅⋅⋅Xn
续例:设计识别 { 0 n 1 n ∣ n ≥ 1 } \{0^n1^n | n ≥ 1\} {0n1n∣n≥1} 的图灵机, 接受 0011 的 ID 序列
解:
q 00011 ⊢ X q 1011 ⊢ X 0 q 111 ⊢ X q 20 Y 1 ⊢ q 2 X 0 Y 1 ⊢ X q 00 Y 1 ⊢ X X q 1 Y 1 ⊢ X X Y q 11 ⊢ X X q 2 Y Y ⊢ X q 2 X Y Y ⊢ X X q 0 Y Y ⊢ X X Y q 3 Y ⊢ X X Y Y q 3 B ⊢ X X Y Y B q 4 B q00011 ⊢ Xq1011 ⊢ X0q111 ⊢ Xq20Y1 ⊢ q2X0Y1 ⊢ Xq00Y1 ⊢ XXq1Y1 ⊢ XXYq11 ⊢ XXq2Y Y ⊢ Xq2XYY ⊢ XXq0YY ⊢ XXYq3Y ⊢ XXYYq3B ⊢ XXYYBq4B q00011⊢Xq1011⊢X0q111⊢Xq20Y1⊢q2X0Y1⊢Xq00Y1⊢XXq1Y1⊢XXYq11⊢XXq2YY⊢Xq2XYY⊢XXq0YY⊢XXYq3Y⊢XXYYq3B⊢XXYYBq4B
19.2 递归可枚举语言
如果 M 是一个图灵机,则 M 接受的语言为
L ( M ) = { w ∣ w ∈ Σ ∗ , q 0 w ⊢ ∗ α p β , p ∈ F , α , β ∈ Γ ∗ } L(M) = \{w | w ∈ Σ^∗, q_0w ⊢*αpβ, p ∈ F, α, β ∈ Γ^∗\} L(M)={w∣w∈Σ∗,q0w⊢∗αpβ,p∈F,α,β∈Γ∗}
如果 L L L 是图灵机 $M $的语言, 即 L = L ( M ) L = L(M) L=L(M), 则称 L L L 是递归可枚举语言.
一般假定, 当输入串被接受时, 图灵机总会停机
然而, 对于不接受的输入, 图灵机可能永远不停止
对接受和不接受的输入, 都保证停机的图灵机, 所接受的语言称为递归语言
19.3 真减法
例:Compute the function nomus (m, n)=max(m-n,0)
解:
19.4 乘法
例:Construct a TM to compute m×n
3 × 2 = 2 + 2 + 2