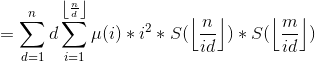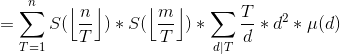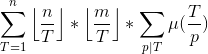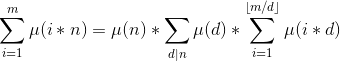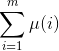莫比乌斯函数
莫比乌斯函数:
其中, pi 表示质数。
性质:
1.
2.
3.
若a,b互质,那么![]()
4.
莫比乌斯反演:
求 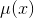 :
:
1. 打表:
//线性筛法求莫比乌斯函数
bool check[MAX+10];
int prime[MAX+10];
int mu[MAX+10];
void Moblus()
{
memset(check,false,sizeof(check));
mu[1] = 1;
int tot = 0;
for(int i = 2; i <= MAX; i++)
{
if( !check[i] ){
prime[tot++] = i;
mu[i] = -1;
}
for(int j = 0; j < tot; j++)
{
if(i * prime[j] > MAX) break;
check[i * prime[j]] = true;
if( i % prime[j] == 0){
mu[i * prime[j]] = 0;
break;
}else{
mu[i * prime[j]] = -mu[i];
}
}
}
}2. 非打表:
ll getmob(ll a){
ll x=a,tmp=a;
int cnt=0,now=0;
for(ll j=2;j*j<=x;j++){
now=0;
if(x%j==0){
while(x%j==0) now++,x/=j;
if(now>1) return 0;
cnt++;
}
}
if(x!=1) cnt++;
return (cnt&1)?-1:1;
}
应用:
1.
这个式子按暴力去算是O(n(1+1/2+1/3+...+1/n)),约等于O(nlogn)的复杂度,往往不能达到要求。可以用数论分块优化成O(n)的复杂度。
本题数论分块方法: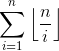 这个形式的式子可用O(sqrt(n))求得,因为该式子只有O(sqrt(n))个值,且若
这个形式的式子可用O(sqrt(n))求得,因为该式子只有O(sqrt(n))个值,且若![]() ,那么在
,那么在 ![]() 范围内
范围内 ![]() 的值均为 k 。因此,先预处理
的值均为 k 。因此,先预处理 ![]() 的前缀和后,本题后面那个累加可以在O(sqrt(n))的复杂度下求得,前面那个累加也可以在O(sqrt(n))下求得,总复杂度为O(n) 。
的前缀和后,本题后面那个累加可以在O(sqrt(n))的复杂度下求得,前面那个累加也可以在O(sqrt(n))下求得,总复杂度为O(n) 。
code:
#include
using namespace std;
typedef long long ll;
const int MAX = 1e7+10;
const ll mod=20101009;
ll n,m;
bool check[MAX];
int prime[MAX];
int mu[MAX];
ll sum[MAX];
void Moblus()
{
memset(check,false,sizeof(check));
mu[1] = 1;
int tot = 0;
for(int i = 2; i <= n; i++)
{
if( !check[i] ){
prime[tot++] = i;
mu[i] = -1;
}
for(int j = 0; j < tot; j++)
{
if(i * prime[j] > n) break;
check[i * prime[j]] = true;
if( i % prime[j] == 0){
mu[i * prime[j]] = 0;
break;
}else{
mu[i * prime[j]] = -mu[i];
}
}
}
sum[0]=0;
for(int i=1;i<=n;i++){
sum[i]=(sum[i-1]+mu[i]*(1ll*i*i%mod)+mod)%mod;
}
}
ll get_g(ll x,ll y)
{
ll tmp1=x*(x+1)/2%mod;
ll tmp2=y*(y+1)/2%mod;
ll ans=tmp1*tmp2%mod;
return ans;
}
ll getlast(ll x,ll y)
{
ll ans=0;
ll pos=0;
for(int i=1;i<=x;i=pos+1){
pos=min(x/(x/i),y/(y/i));
ans=(ans+(sum[pos]-sum[i-1]+mod)%mod*get_g(x/i,y/i)%mod)%mod;
}
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
if(n>m) swap(n,m);
Moblus();
ll ans=0;
ll pos=0;
for(int i=1;i<=n;i=pos+1){
pos=min(n/(n/i),m/(m/i));
ans=(ans+1ll*(i+pos)*(pos-i+1)/2%mod*getlast(n/i,m/i)%mod)%mod;
}
printf("%lld\n",ans);
return 0;
}
如果本题有多组数据,那么还可以O(n)预处理,每次询问O(sqrt(n))。
因为 ![]() 和
和 ![]() 都是积性函数,所以他们的狄利克雷卷积也是积性函数,即
都是积性函数,所以他们的狄利克雷卷积也是积性函数,即![]() 为积性函数,所以可以用线性筛预处理它的前缀和,然后等式前半段通过对
为积性函数,所以可以用线性筛预处理它的前缀和,然后等式前半段通过对 ![]() 的数论分块O(sqrt(n))求得,因此单次询问复杂度O(sqrt(n))。
的数论分块O(sqrt(n))求得,因此单次询问复杂度O(sqrt(n))。
code:
#include
using namespace std;
typedef long long ll;
const int MAX = 1e7+10;
const ll mod=20101009;
ll n,m;
ll sum[MAX],check[MAX],prime[MAX];
void get_sum()
{
memset(check,0,sizeof(check));
sum[1]=1;
int tot=0;
for(int i=2;i<=n;i++){
if(!check[i]){
prime[tot++]=i;
sum[i]=(i-1ll*i*i%mod+mod)%mod;
}
for(int j=0;jm) swap(n,m);
ll pos=0;
ll ans=0;
for(int i=1;i<=n;i=pos+1){
pos=min(n/(n/i),m/(m/i));
ll tmp=((n/i)*(n/i+1)/2%mod)*((m/i)*(m/i+1)/2%mod)%mod;
ans=(ans+(sum[pos]-sum[i-1]+mod)%mod*tmp%mod)%mod;
}
printf("%lld\n",ans);
return 0;
}
2.
求 ![\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=p]](http://img.e-com-net.com/image/info8/c1e4f2668faa4ae98fc42a34ff1100ed.gif) , p为质数,n,m<=1e7,1000组询问 。 (洛谷2257)
, p为质数,n,m<=1e7,1000组询问 。 (洛谷2257)
推导过程略。
后半部分预处理,前半部分数论分块,每次查询O(sqrt(n)) 。
#include
using namespace std;
typedef long long ll;
const int MAX = 10000000;
const ll MOD = 1000000007;
ll mu[MAX+10],prime[MAX+10];
ll sum[MAX];
bool check[MAX+10];
inline int read()
{
int x=0,t=1;register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')t=-1,ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
return x*t;
}
//预处理前缀和
void get_sum()
{
memset(check,false,sizeof(check));
mu[1]=1;
int tot=0;
for(int i=2;i<=MAX;i++){
if(!check[i]){
prime[tot++]=i;
mu[i]=-1;
}
for(int j=0;jm) swap(n,m);
int pos;
ll ans=0;
//数论分块
for(int i=1;i<=n;i=pos+1){
pos=min(n/(n/i),m/(m/i));
ans+=1ll*(n/i)*(m/i)*(sum[pos]-sum[i-1]);
}
printf("%lld\n",ans);
}
return 0;
}
递归终止条件:
m=0:f(m,n)=0
m=1:f(m,n)=![]()
代码:
#include
using namespace std;
typedef long long ll;
const int MAX = 1e7;
ll mu[MAX+10],prime[MAX+10];
bool check[MAX+10];
void get_sum()
{
memset(check,false,sizeof(check));
mu[1]=1;
int tot=0;
for(int i=2;i<=MAX;i++){
if(!check[i]){
prime[tot++]=i;
mu[i]=-1;
}
for(int j=0;jdp;
//杜教筛
ll cal(ll x)
{
if(x<=MAX) return mu[x];
if(dp[x]) return dp[x];
ll pos;
ll tmp=0;
for(ll i=2;i<=x;i=pos+1){
pos=x/(x/i);
tmp+=(pos-i+1)*cal(x/i);
}
return dp[x]=1-tmp;
}
int cnt[5000];
ll val[5000];
ll p[20];
int pnum;
ll u(ll x)
{
return ((cnt[x]&1)?-1:1);
}
ll dfs(ll m,ll n)
{
if(cnt[n]==0) return cal(m);
if(m==0) return 0;
if(m==1) return u(n);
ll ans=0;
//遍历n的所有因子
for(int i=n;;i=(i-1)&n){
ans+=u(i)*dfs(m/val[i],i);
if(!i) break;
}
return ans*u(n);
}
int main()
{
get_sum();
ll m,n;
scanf("%lld%lld",&m,&n);
int fg=0;
pnum=0;
for(ll i=2;i*i<=n;i++){
if(n%i==0){
ll tmp=i*i;
if(n%tmp==0) {fg=1;break;}
p[pnum++]=i; //处理出所有素因子
while(n%i==0) n/=i;
}
}
if(fg){
printf("0\n");
}
else{
if(n>1) p[pnum++]=n;
for(int i=0;i<(1<
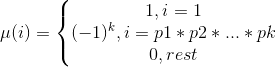
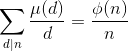
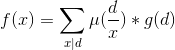
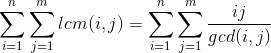
![=\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{d=1}^{n}[gcd(i,j)=d]*\frac{ij}{d}=\sum_{d=1}^{n}\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=d]*\frac{ij}{d}](http://img.e-com-net.com/image/info8/b2bef7941a40429f989e1a4039aab386.gif)
![f(k)=\sum_{i=1}^{x}\sum_{j=1}^{y}[gcd(i,j)=k]*i*j](http://img.e-com-net.com/image/info8/c129a930695347feb0190ad81606989d.gif)

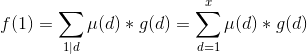
![g(k)=\sum_{k|d}^{ }f(d)=\sum_{k|d}^{ }\sum_{i=1}^{x}\sum_{j=1}^{y}[gcd(i,j)=d]*i*j](http://img.e-com-net.com/image/info8/e9426b8b7ee84e129b9a63185b344993.gif)
![=\sum_{i=1}^{x}\sum_{j=1}^{y}[k|gcd(i,j)]*i*j=\sum_{i=1}^{\left \lfloor \frac{x}{k} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{y}{k} \right \rfloor}[1|gcd(i,j)]*i*j*k^{2}](http://img.e-com-net.com/image/info8/bf9a01898e48477d89c55c5df9a6e1cb.gif)
![=k^{2}\sum_{i=1}^{\left \lfloor \frac{x}{k} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{y}{k} \right \rfloor}[1|gcd(i,j)]*i*j](http://img.e-com-net.com/image/info8/dccf117d2b88471aa8ca12a638fef6ea.gif)