概率与期望的学习
目录
一些公式
P1291 [SHOI2002]百事世界杯之旅
[WOJ3010] 骰子
[WOJ3007] Dumb Bones
[WOJ2276]挑战
[WOJ3806]收集邮票
[WOJ3083] 收集宝石
[WOJ3080]迷宫
[WOJ2658]单机游戏
[WOJ1111] 钉子和小球
简单游戏
P3211 [HNOI2011]XOR和路径
P2473 [SCOI2008]奖励关
[WOJ3481]Slay the Spire (稍难)
[WOJ3804]Easy
[WOJ3805]OSU
P3232 [HNOI2013]游走
一些公式
全概率公式
对于互不相容的事件B, 一个随机事件A
期望
理解一下这个
例:抛一个骰子,求抛到6期望多少次
设Xk为抛k次抛到6的期望
当然, 因为 P(抛到6) 为 1/6, 所以期望自然是6
全期望公式
计算期望的方法:1. 直接计算 2. 递推 或 DP 3. 迭代计算 4. 建立方程组
概率期望的最值问题一般用DP解决
P1291 [SHOI2002]百事世界杯之旅
考虑当前抽的, 有 x/n 的概率与前面的重复, n-x / n 的概率可以使人数多一个
于是当前的期望就是上一步的期望 + 上一步到这一步的期望,也就是 1 / (n-x / n)
//一个不全的代码
#include
using namespace std;
int gcd(int x,int y){ return !y ? x : gcd(y, x%y);}
struct Node{
int x, y;
friend Node operator + (const Node &a, const Node &b){
Node c; int g = gcd(a.y, b.y);
c.y = a.y / g * b.y;
int k1 = a.y / g, k2 = b.y / g;
c.x = a.x * k2 + b.x * k1;
return c;
}
}f[40]; int n;
int main(){
scanf("%d", &n); f[1].x = f[1].y = 1;
for(int i=1; i [WOJ3010] 骰子
f[i][j] 表示投了i次,和为j的个数,最后除以6^n输出就可以了
#include
#define LL long long
using namespace std;
LL tot=1, ans, f[30][200]; int n, x;
LL gcd(LL a,LL b){ return !b ? a : gcd(b, a%b);}
int main(){
scanf("%d%d", &n, &x); f[0][0] = 1;
for(int i=1; i<=n; i++){ tot *= 6;
for(int j=1; j<=i*6; j++){
for(int k=1; k<=6; k++){
if(j - k >= 0) f[i][j] += f[i-1][j-k];
}
}
}
for(int i=x; i<=n*6; i++) ans += f[n][i];
LL g = gcd(tot, ans);
if(ans/g == 0) cout << "0";
else if(ans/g == 1 && tot/g == 1) cout << "1";
else cout << ans/g << "/" << tot/g < [WOJ3007] Dumb Bones
概率 + 最优, 很明显是一个区间DP
我们单纯地考虑一个区间,枚举区间的断点,那么当前区间的期望就是
解释一下,当前位置期望放 1 / (1-pl-pr) 次是显然的,然后左右各期望重构 pl / (1-pl-pr), pr / (1-pl-pr) 次
于是, 我们用 f(k) 表示长度为 k 的区间的答案, 然后枚举中间点更新就可以了
#include
#define N 1050
using namespace std;
double f[N], pl, pr; int n;
double Solve(){
for(int i=0; i<=n; i++) f[i] = 0;
for(int i=1; i<=n; i++){
double ans = 0x3fffffff;
for(int j=0; j [WOJ2276]挑战
如果不考虑碎片的限制, f[i][j] 表示 前i个 有j个成功的概率
![]()
![]()
然后加一维就可以了, 注意到背包容量到 n就足够了,所以第3位只用枚举到n
#include
#define N 205
using namespace std;
int n, a[N], L, K; double f[N][N][N<<1], p[N];
int main(){
scanf("%d%d%d", &n, &L, &K);
for(int i=1; i<=n; i++){
scanf("%lf", &p[i]); p[i] /= 100.0;
}
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
if(K > n) K = n;
f[0][0][K+200] = 1;
for(int i=0; i [WOJ3806]收集邮票
我们先简单地考虑
令 f[i] 表示已经选了i张, 选到n张的期望张数
令g[i] 为已经选了i张, 选到n张的期望价格 ,我们姑且令当前买的价格为1, 后面买的价格都 +1,那么总价格就加了f[i] + 1
#include
#define N 10050
using namespace std;
double f[N], g[N], n;
int main(){
scanf("%lf",&n);
for(int i=n-1; i>=0; i--){
f[i] = f[i+1] + (n / (n-i));
g[i] = f[i+1] + g[i+1] + f[i] * i / (n-i) + (n / (n-i));
} printf("%0.2lf", g[0]); return 0;
} [WOJ3083] 收集宝石
类似前面的套路, f[i][j] 表示 有i种宝石,从j个洞里挖出来的期望
#include
#define N 1005
using namespace std;
double f[N][N], n, s;
int main(){
scanf("%lf%lf", &n, &s);
for(int i=n; i>=0; i--){
for(int j=s; j>=0; j--){
if(i==n && j==s) continue;
if(j+1 <= s) f[i][j] += (f[i][j+1] * (i/n) * (1-j/s)) / (1 - (i/n) * (j/s));
if(i+1 <= n) f[i][j] += (f[i+1][j] * (1-i/n) * (j/s)) / (1 - (i/n) * (j/s));
if(j+1 <= s && i+1 <= n) f[i][j] += (f[i+1][j+1] * (1-i/n) * (1-j/s)) / (1 - (i/n) * (j/s));
f[i][j] += 1 / (1 - (i/n) * (j/s));
}
} printf("%0.4lf", f[0][0]);
} [WOJ3080]迷宫
题目明确了图是一棵树, 我们把蓝宝石作为根, 就是求每个点到根的期望
我们先考虑每个点到父亲的期望, 不妨设为 f(u)
加上父亲的1步, ![]()
设到根的期望为 E(u)
![]()
#include
#define N 6000
#define M 55
using namespace std;
int first[N], nxt[N], to[N], tot;
char Map[M][M]; int n, m, rt, E[N], f[N], sum, cnt;
int pos(int i,int j){ return (i-1) * n + j;}
int fx[5] = {0, 1, -1, 0, 0};
int fy[5] = {0, 0, 0, 1, -1};
void add(int x,int y){nxt[++tot] = first[x], first[x] = tot, to[tot] = y;}
void dfs(int u, int fa){
f[u] = 1;
for(int i=first[u];i;i=nxt[i]){
int t = to[i]; if(t == fa) continue;
dfs(t, u); f[u] += f[t] + 1;
} if(!fa) f[u] = 0;
}
void dfs2(int u,int fa){
E[u] = f[u] + E[fa];
for(int i=first[u];i;i=nxt[i]){
int t = to[i]; if(t == fa) continue; dfs2(t, u);
} sum += E[u];
}
int main(){
scanf("%d%d", &n, &m); cnt = m * n;
for(int i=1; i<=n; i++) scanf("%s", Map[i]+1);
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
if(Map[i][j] == 'X'){ cnt--; continue;}
if(Map[i][j] == '*') rt = pos(i, j);
for(int k=1; k<=4; k++){
int x = i + fx[k], y = j + fy[k];
if(x>=1 && x<=n && y>=1 && y<=m && Map[x][y] != 'X'){
add(pos(i, j), pos(x, y));
}
}
}
} dfs(rt, 0); dfs2(rt, 0); printf("%0.2lf",sum / (cnt*1.0));
return 0;
} [WOJ2658]单机游戏
f[i][j] 表示还剩i张红和j张黑的期望
记得小于0了就变成0
#include
#define N 1050
using namespace std;
int n, m; double f[N][N];
int main(){
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++){
f[i][0] = i;
for(int j=1; j<=m; j++){
f[i][j] = (i / ((i+j) * 1.0) * (f[i-1][j] + 1)) + (j / ((i+j) * 1.0) * (f[i][j-1] - 1));
f[i][j] = max(f[i][j], 0.0);
}
} printf("%0.8lf", f[n][m]);
} [WOJ1111] 钉子和小球
不妨放下来2 ^ n 个球, f[i][j] 表示到 i, j的方案数, 转移刷表就可以了
#include
#define N 1005
#define LL long long
using namespace std;
LL f[N][N], tot; int n, m;
char Map[N][N];
LL gcd(LL a, LL b){ return !b ? a : gcd(b, a%b);}
int main(){
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++){
for(int j=1; j<=i; j++) scanf("%s",&Map[i][j]);
} f[1][1] = tot = (1ll << n);
for(int i=1; i<=n; i++){
for(int j=1; j<=i; j++){
if(Map[i][j] == '.') f[i+2][j+1] += f[i][j];
else{
f[i+1][j] += f[i][j] / 2;
f[i+1][j+1] += f[i][j] / 2;
}
}
} LL g = gcd(tot, f[n+1][m+1]);
cout << f[n+1][m+1] / g << "/" << tot / g;
return 0;
}
简单游戏
所谓简单游戏,相信大家小时候都玩过,就是那种掷出股子子,然后按掷的步数走的游戏。
现在有一个n(1≤n≤100)个格子的游戏,一些格子上有指令。指令分成若干种,如下:
0—空指令 -1—陷阱,到了这里后要掷出六才能继续向前,注意不是向前六步,而是要再掷一次决定步数。 -2—停一次
其它数字 ---- 转移指令,走到数字所代表的格子
走到陷阱中是很难出来的,因此大家都不希望走到陷阱里。
玩一次游戏走到陷阱里的平均次数到底是多少呢?这个问题将由你来解决。
[输入格式]
第一行n,表示游戏的格数。
第二行有n个数,表示每个格子的指令(第一个和最后一个都没有指令)。注意如果某次走到的位置达到或超过最后一个格子,
都表示游戏结束。
[输出格式] 输出走到陷阱里的平均次数。保留3位小数。
[样例输入] 4 0 -1 2 0 [样例输出] 0.400
不会做先建图, 每个点朝可以到达的点连边, 边权为走这条边的概率
我们用 Ei 表示到达过Ei的概率
![]()
解得 E2 = 0.4
高斯消元就可以了, 所有陷阱的E的和就是答案
#include
#define N 500
using namespace std;
int first[N], nxt[N], to[N], tot; double w[N];
int n, vis[N]; double a[N][N];
void add(int x,int y,double z){
if(y > n) return;
nxt[++tot] = first[x], first[x] = tot;
to[tot] = y, w[tot] = z;
}
void gauss(){
for(int i=1; i<=n; i++){
int k = i;
for(int j=i+1; j<=n; j++)
if(fabs(a[j][i]) > fabs(a[k][i])) k = j;
for(int j=i; j<=n+1; j++) swap(a[k][j], a[i][j]);
double res = a[i][i];
for(int j=i; j<=n+1; j++) a[i][j] /= res;
for(int j=1; j<=n; j++){
if(j != i){
double tmp = a[j][i];
for(int k=i; k<=n+1; k++) a[j][k] -= a[i][k] * tmp;
}
}
}
}
int main(){
scanf("%d", &n);
for(int i=1; i<=n; i++){
int x; scanf("%d",&x);
if(x == 0 || x == -2){
for(int k=1; k<=6; k++) add(i+k, i, 1.0/6);
}
else if(x == -1){
vis[i] = 1;
for(int k=1; k<=6; k++) add(i+k, i, 1.0/6);
}
else add(x, i, 1);
} a[1][n+1] = -1;
for(int i=1; i<=n; i++){
for(int e=first[i];e;e=nxt[e]){
int t = to[e]; a[i][t] = w[e];
} a[i][i] = -1;
} gauss(); double ans = 0;
for(int i=1; i<=n; i++)
if(vis[i]) ans += a[i][n+1] / a[i][i];
printf("%0.2lf",ans); return 0;
} P3211 [HNOI2011]XOR和路径
异或一般按位考虑
我们令E(x) 位当前位,到n 的异或和位1的概率
高斯消元就可以了
#include
#define N 105
#define M 20050
using namespace std;
int first[N], nxt[M], to[M], w[M], tot;
int n, m, du[N], Max;
double a[N][N], ans;
void add(int x, int y,int z){
nxt[++tot] = first[x], first[x] = tot;
to[tot] = y, w[tot] = z, du[y]++;
}
void gauss(){
for(int i=1; i<=n; i++){
int k = i;
for(int j=i+1; j<=n; j++)
if(fabs(a[j][i]) > fabs(a[k][i])) k = i;
for(int j=1; j<=n+1; j++) swap(a[k][j], a[i][j]);
double res = a[i][i];
for(int j=i; j<=n+1; j++) a[i][j] /= res;
for(int j=1; j<=n; j++){
if(j == i) continue;
double tmp = a[j][i];
for(int k=i; k<=n+1; k++) a[j][k] -= tmp * a[i][k];
}
}
}
int main(){
scanf("%d%d", &n, &m);
for(int i=1; i<=m; i++){
int x, y, z; scanf("%d%d%d", &x, &y, &z);
if(x == y) add(x, y, z);
else add(x, y, z), add(y, x, z);
Max = max(Max, z);
}
for(int i=1; i<=Max; i<<=1){
memset(a, 0, sizeof(a));
for(int j=1; j P2473 [SCOI2008]奖励关
题目要求最优, 这启示我们用DP来解决
f [u][S] 表示选了u个,状态为S的期望
如果可以选i
否则
#include
#define N 105
#define M (1<<15)
using namespace std;
double f[N][M], val[N];
int s[N], n, k;
double dfs(int u,int S){
if(u >= k) return 0;
if(f[u][S] != -1) return f[u][S];
double res = 0;
for(int i=1; i<=n; i++){
if((s[i] & S) == s[i]) res += max(dfs(u+1, S|(1<<(i-1))) + val[i], dfs(u+1, S));
else res += dfs(u+1, S);
}
return f[u][S] = res / (n*1.0);
}
int main(){
scanf("%d%d", &k, &n);
for(int i=1; i<=n; i++){
scanf("%lf", &val[i]);
int x; while(1){
scanf("%d", &x); if(!x) break;
s[i] |= (1<<(x-1));
}
} for(int i=0; i<=k; i++) for(int j=0; j<=(1< [WOJ3481]Slay the Spire (稍难)
首先得会暴力,我们dfs全排列一下,然后对于当前选出来的数,我们令选i张强化卡, m-i张攻击卡,有个很明显的贪心就是
当 i >= k 时, 选k-1张强化卡,1张攻击卡
当 i < k 时,选 i 张强化卡,k-i张攻击卡
这启示我们先将卡牌按攻击力与强化值从大到小排序, 然后怎么做呢?只能用DP计数了
我们令F(i,j) 表示随机选i个,从i个中选j个强化卡的期望倍数
G(i,j) 表示表示随机选i个,从i个中选j个强化卡的期望攻击力
这样还是不能转移
我们可以枚举最后出现的位置r
其中 f (j,r) 表示选j个, 最后一个在r的期望,因为最后的都在r,所以后面的i-j个只能在n-r个位置中全排列
现在考虑如何处理 f,g, 考虑当前位接到哪个后面
对于g, 考虑当前值有多少贡献
前缀和优化可以O(n^2), 然后不用处理全部的F, G,要哪些处理哪些
#include
#define N 3050
#define Mod 998244353
#define LL long long
using namespace std;
LL f[N][N], g[N][N], c[N][N], Sf[N], Sg[N];
int T, n, m, k, a[N], b[N];
void prework(){
for(int i=0; i<=N-50; i++){
c[i][0] = 1;
for(int j=1; j<=i; j++){
c[i][j] = (c[i-1][j] + c[i-1][j-1]) % Mod;
}
}
}
void Init(){
memset(f, 0, sizeof(f));
memset(g, 0, sizeof(g));
memset(Sf, 0, sizeof(Sf));
memset(Sg, 0, sizeof(Sg));
}
bool cmp(int a,int b){ return a > b;}
LL F(int a, int b){
LL ans = 0;
for(int i=b; i<=n; i++){
ans = (ans + c[n-i][a-b] * f[b][i] % Mod) % Mod;
} return ans;
}
LL G(int a,int b){
LL ans = 0;
for(int i=b; i<=n; i++){
ans = (ans + c[n-i][a-b] * g[b][i] % Mod) % Mod;
} return ans;
}
int main(){
scanf("%d", &T); prework();
while(T--){
scanf("%d%d%d", &n, &m, &k); Init();
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
for(int i=1; i<=n; i++) scanf("%d", &b[i]);
sort(a+1, a+n+1, cmp); sort(b+1, b+n+1, cmp);
f[0][0] = 1;
for(int i=1; i<=n; i++) f[1][i] = a[i], g[1][i] = b[i];
for(int i=2; i<=n; i++){
for(int j=i; j<=n; j++){
Sf[i-1] = (Sf[i-1] + f[i-1][j-1]) % Mod;
f[i][j] = Sf[i-1] * a[j] % Mod;
Sg[i-1] = (Sg[i-1] + g[i-1][j-1]) % Mod;
g[i][j] = (Sg[i-1] + (b[j] * c[j-1][i-1]) % Mod) % Mod;
}
}
LL ans = 0;
for(int i=0; i<=m && i<=n; i++){ // 选i张强化牌
if(m - i > n) continue;
if(i >= k) ans = (ans + F(i, k-1) * G(m-i, 1) % Mod) % Mod;
else ans = (ans + F(i, i) * G(m-i, k-i) % Mod) % Mod;
} printf("%lld\n", ans);
} return 0;
} [WOJ3804]Easy
L(x)表示期望长度,E(x) 表示期望价值,分情况转移就可以了
#include
#define N 300050
using namespace std;
double L[N], E[N];
int n; char s[N];
int main(){
scanf("%d%s", &n, s+1); L[n+1] = E[n+1] = 0;
for(int i=n; i>=1; i--){
if(s[i] == 'o'){
L[i] = L[i+1] + 1;
E[i] = E[i+1] + 2 * L[i+1] + 1;
}
if(s[i] == 'x'){
L[i] = 0; E[i] = E[i+1];
}
if(s[i] == '?'){
L[i] = (L[i+1] + 1) / 2.0;
E[i] = E[i+1] + (2 * L[i+1] + 1)/ 2.0;
}
} printf("%0.4lf", E[1]); return 0;
} [WOJ3805]OSU
跟上道题差不多,唯一需要注意的是平方的期望不是期望的平方,所以还有维护L^2的期望
#include
#define N 100050
using namespace std;
double L[N], E[N], L2[N], p[N]; int n;
int main(){
scanf("%d", &n); L[n+1] = E[n+1] = 0;
for(int i=1; i<=n; i++) scanf("%lf",&p[i]);
for(int i=n; i>=1; i--){
L2[i] = p[i] * (L2[i+1] + 2 * L[i+1] + 1);
E[i] = p[i] * (E[i+1] + 3 * L2[i+1] + 3 * L[i+1] + 1) + (1 - p[i]) * E[i+1];
L[i] = p[i] * (L[i+1] + 1);
} printf("%0.1lf", E[1]); return 0;
} P3232 [HNOI2013]游走
由于经过某条变的概率不好算,而且边太多,我们转换为求每个点的概率
点1与点n有些特殊, 由于"游走"是从点1开始,则计算点1期望时实际期望应该是原期望+1
若有点和n相连,那么在计算期望时是不需要将其算入的,因为到了点n的时候是不会继续"游走"了
#include
#define N 505
#define M (N*N*2)
using namespace std;
int first[N], nxt[M], to[M], du[N], tot;
void add(int x,int y){
nxt[++tot] = first[x], first[x] = tot;
to[tot] = y, du[y]++;
}
int n, m, x[M], y[M];
double a[N][N], val[N], p[M];
void gauss(){
for(int i=1; i<=n; i++){
int k = i;
for(int j=i+1; j<=n; j++)
if(fabs(a[j][i]) > fabs(a[k][i])) k = j;
for(int j=1; j<=n+1; j++) swap(a[i][j], a[k][j]);
double res = a[i][i];
for(int j=i; j<=n+1; j++) a[i][j] /= res;
for(int j=1; j<=n; j++){
if(i == j) continue;
double tmp = a[j][i];
for(int k=i; k<=n+1; k++) a[j][k] -= tmp * a[i][k];
}
}
for(int i=1; i<=n; i++) val[i] = a[i][n+1] / a[i][i];
}
int main(){
scanf("%d%d", &n, &m);
for(int i=1; i<=m; i++){
scanf("%d%d",&x[i], &y[i]);
add(x[i], y[i]); add(y[i], x[i]);
}
n--; a[1][n+1] = 1;
for(int i=1; i<=n; i++){ a[i][i] = 1;
for(int e = first[i]; e; e=nxt[e]){
int t = to[e]; if(t <= n)
a[i][t] = -1.0 / du[t]*1.0;
}
} gauss();
for(int i=1; i<=m; i++){
if(x[i] <= n) p[i] += val[x[i]] / du[x[i]];
if(y[i] <= n) p[i] += val[y[i]] / du[y[i]];
} sort(p+1, p+m+1);
double ans = 0;
for(int i=1; i<=m; i++){
ans += p[i] * (m-i+1);
} printf("%0.3lf", ans); return 0;
}
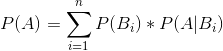





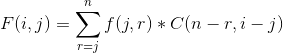

![f(i,j)=a[j]*\sum_{r=i-1}^{j-1}f(i-1,r)](http://img.e-com-net.com/image/info8/4602c85fba82405ba9e50d770ce12a0d.gif)
![g(i,j)=a[j]*C(j-1,i-1)+\sum_{r=i-1}^{j-1}g(i-1,r)](http://img.e-com-net.com/image/info8/0a37551810ae47239b70601dd0386b26.gif)