算法分析与设计:图的搜索算法
一、图的两种基本遍历
1. 邻接矩阵与邻接表
图的储存方式通常有两种:邻接矩阵和邻接表。
● 邻接矩阵
最简单的图的表示方式。它通过一个二维数组模拟矩阵,来储存图的信息。
对于无权图,矩阵元素a[i][j]标识顶点 i 到顶点 j 的邻接信息。若为1则邻接;为0则不邻接。
对于带权图,矩阵元素a[i][j]标识顶点 i 到顶点 j 的权值,并通常用 ∞ (INT_MAX) 标志不邻接的顶点权值。
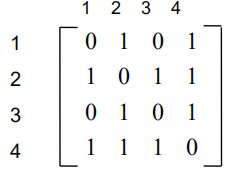

在稀疏图中,邻接矩阵会造成矩阵空间的大量浪费,这时可以采用压缩策略(如十字链表法)来储存矩阵。
//邻接矩阵定义
struct Graph{
int **arcs; //矩阵
int *vexs; //顶点向量
int vernum; //顶点数
int arcnum; //弧数
};
● 邻接表
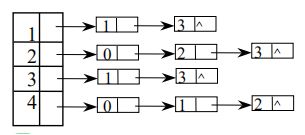
为方便地找到邻接点,我们将每个顶点的边用一个单链表储存,并连接在源顶点的头结点上。所有的头结点保存在一个一维数组中,这样就可以得到若干个存有图内信息的单链表。如此得到的整个数据结构叫做邻接表。
//邻接表的定义
struct arcNode{ //弧结点的定义
int adjVex; //邻接的另一个顶点的编号或下标
arcNode *nextArc; //源顶点的下一条弧
};
struct vexNode{ //顶点结点的定义
int number; //顶点编号
arcNode *firstArc; //该顶点的第一条弧
};
struct Graph{
vexNode *vexs; //顶点数组
int vexnum;
int arcnum;
};
● 两者的比较
| 优点 | 缺点 | |
|---|---|---|
| 邻接矩阵 | 适合查找两点之间是否相连,并得到两点之间权值 | 寻找某一个点的邻接顶点需要搜索整行或整列 |
| 邻接表 | 容易查找某一个顶点的所有邻接点 | 判断顶点间是否相邻需要搜索一个单链表 |
邻接表易于根据一个顶点,找到它所有邻接的顶点,因此它很适合用于图的搜索算法中。下面的算法均使用邻接表储存图。
2. 广度优先搜索遍历
● 基本思想
广度优先搜索简称BFS,是从图中一个源顶点v0出发,找到源顶点所有的邻接点,然后再对所有找到邻接顶点,找到它们各自的邻接顶点。到v0距离短(经过定点少)的顶点更优先被遍历,就好像根据当前顶点的宽广度(邻接的顶点数)向外扩散一样。
为使算法对非连通图也有效,我们可以在每次搜索后检查顶点情况,将未访问的顶点作为下一个源顶点继续搜索。
为实现广度优先搜索,我们可以使用队列来保存需要搜索的顶点。
为避免对顶点的重复遍历,另设一个数组,标记顶点是否被遍历过。
算法描述如下:
- 给定一个图和起始顶点,标记起始顶点并入队列
- 从队列中弹出一个顶点,并查找其所有的邻接顶点;被查找到的顶点若已被标记,则舍弃;否则标记并入队列
- 重复步骤2,直到队列为空
● 算法实现
//BFS
void traverseBFS(Graph G, int start, bool *isVisited) //利用队列搜索
{
queue<int> q;
q.push(start);
isVisited[start] = true;
visit(start); //遍历时期望做的操作
while(!q.empty()){
int v = q.front();
q.pop();
arcNode *p = G.vexs[v].firstArc;
while(p != nullptr){
if(!isVisited[p->adjVex]){
visit(p->adjVex);
isVisited[p->adjVex] = true;
q.push(p->adjVex);
}
p = p -> nextArc;
}
}
}
void BFS(Graph G) //BFS函数,可以遍历非连通图
{
bool isVisited[G.vexnum] = {false};
for(int i = 0;i < G.vexNum;i++){ //检查顶点
if(!isVisited[i])
traverseBFS(G,i,isVisited);
}
}
● 时间复杂度
设顶点数为V,弧数为E。BFS中for循环需要执行V次,而traverseBFS中最内层的语句需要执行E次(搜索整个邻接表)。
因此广度优先搜索的时间复杂度为O(V+E)。
3. 深度优先搜索遍历
● 基本思想
深度优先搜索简称DFS,是从图中一个源顶点V0出发,找到它的一个邻接点,若邻接点未被访问过,则进入该邻接点,并继续找它的邻接点;若一个点的邻接点全部被访问过,则回溯到上一顶点,找它的下一邻接点。这一算法的过程就好像往图的深处搜索一样。
为实现深度优先搜索,可以使用栈来保存顶点,也可以采用递归的方式。
类似于BFS,需要一个数组标记顶点是否被遍历过。
算法描述如下:
- 给定一个图和起始顶点,标记起始顶点并入栈(入递归函数)
- 找到栈顶顶点的下一个邻接点:若未访问,标记并入栈(递归);否则舍弃
- 若顶点没有下一个邻接点,弹出顶点,回溯至上一顶点
- 重复步骤2,直到栈为空
● 算法实现
- 递归方式
//DFS Rec
void traverseDFSRec(Graph G,int v,bool *isVisited) //递归函数
{
isVisited[v] = true;
visit(v);
arcNode *p = G.vexs[v].firstArc;
while(p != nullptr){
if(!isVisited[p->adjVex])
traverseDFSRec(G,p->adjVex,isVisited);
p = p->nextArc;
}
}
void DFS(Graph G) //DFS函数
{
bool isVisited[G.vexnum] = {false};
for(int i = 0;i < G.vexnum;i++){ //检查顶点
if(!isVisited[i])
traverseDFS(G,i,isVisited);
}
}
- 栈方式
在栈方式中,需要另设一个数组,标记各个栈内元素当前搜索的位置
//DFS Stack
void traverseDFS(Graph G,int start, bool *isVisited) //栈方式深度优先搜索
{
stack<int> s;
arcNode *iterators[G.vexnum];
for(int i = 0;i < G.vexnum;i++){ //初始化迭代器数组
iterators[i] = G.vexs[i].firstArc;
}
s.push(start);
isVisited[start] = true;
visit(start);
while(!s.empty()){
int v = s.top();
if(iterators[v] != nullptr){ //迭代器不为空,栈顶元素可找到下一邻接点
int adj = iterators[v]->adjVex;
if(!isVisited[adj]){ //邻接点未访问
s.push(adj);
isVisited[adj] = true;
visit(adj);
}
iterators[v] = iterators[v]->nextArc;
}
else{ //迭代器为空,弹出栈顶元素
s.pop();
}
}
}
void DFS(Graph G) //DFS函数
{
bool isVisited[G.vexnum] = {false};
for(int i = 0;i < G.vexnum;i++){ //检查顶点
if(!isVisited[i])
traverseDFSRec(G,i,isVisited);
}
}
● 时间复杂度
设顶点数为V,弧数为E。DFS中for循环需要执行V次。对于递归方式和栈方式,需要while循环内语句共执行E次。
因此深度优先搜索的时间复杂度为O(V+E)。
二、典型问题
有向无环图的拓扑排序
● 问题描述
不存在回边的有向图称为有向无环图,简称DAG图。
DAG图有特殊的一类AOV网,其定义为:顶点表示活动,弧表示活动间的优先关系的有向无环图。
AOV网常用于工程的计划和管理等方面。要判断工程能否有效运行,就是要求解拓扑排序。
所谓拓扑排序,就是分析AOV网络,将活动的优先次序以线性方式列出来的过程。
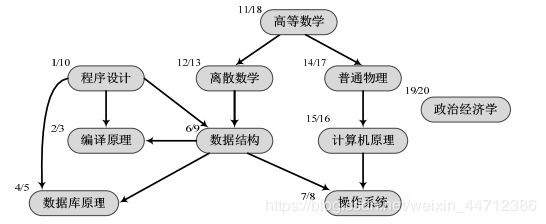
● 基本思想
拓扑排序有两种处理的办法:一是每次在图中查找入度为0的顶点;二是利用深度优先得到一个反向的拓扑顺序。
● 算法实现
//方法一:查找入度为0的顶点
int* topLogicalSort(Graph G)
{
bool isVisited[G.vexnum] = {false};
int inDeg[G.vexnum] = {0};
//获取入度
for(int i = 0;i < G.vexnum;i++){
arcNode* p = G.vexs[i].firstArc;
while(p != nullptr){
inDeg[p->adjVex]++;
p = p->nextArc;
}
}
int* ans = new int[G.vexnum];
int index = 0;
//开始排序
while(index < G.vexnum){
int cur = -1;
for(int i = 0;i < G.vexnum;i++){ //找到入度为0的顶点
if(!isVisited[i] && inDeg[i] == 0){
cur = i;
break;
}
}
if(cur == -1) //排序不可推进,说明存在环
return nullptr;
ans[index] = cur; //写入答案
++index;
isVisited[cur] = true;
arcNode* p = G.vexs[cur].firstArc;
while(p != nullptr){ //将写入的点删除,更新入度
inDeg[p->adjVex]--;
p = p->nextArc;
}
}
return ans;
}
//方法二:深度优先
int* topLogicalSortDFS(Graph G)
{
bool isVisited[G.vexnum] = {false};
arcNode *iterators[G.vexnum];
for(int i = 0;i < G.vexnum;i++){ //初始化迭代器数组
iterators[i] = G.vexs[i].firstArc;
}
int *ans = new int[G.vexnum];
stack<int> s;
int index = G.vexnum - 1;
for(int i = 0;i < G.vexnum;i++){
if(!isVisited[i]){
isVisited[i] = true;
s.push(i);
while(!s.empty()){
int v = s.top();
if(iterators[v] != nullptr){
int adj = iterators[v]->adjVex;
if(!isVisited[adj]){
s.push(adj);
isVisited[adj] = true;
}
iterators[v] = iterators[v]->nextArc;
}
else{ //结束点
s.pop();
ans[index--] = v;
}
}
}
}
return ans;
}