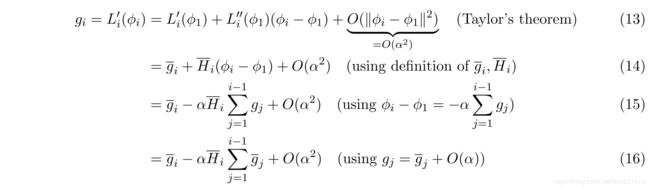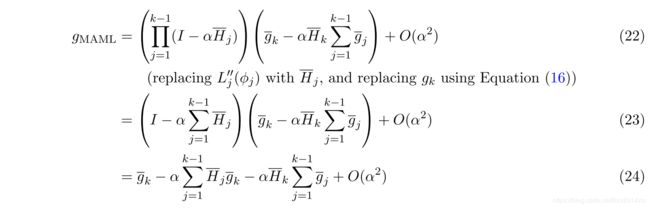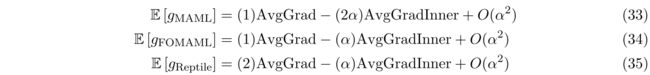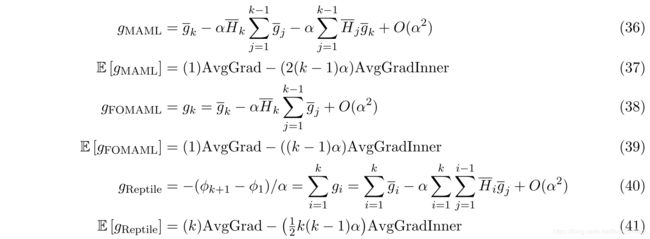Reptile

Paper : On First-Order Meta-Learning Algorithms
Code :

摘要

作者仿照FOMAML(一阶近似MAML)的方法提出了Reptile算法进行元学习，Reptile与FOMAML同样只利用了一阶梯度信息，但是理论分析了Reptitle可以使用SGD对二阶梯度信息进行近似，因此相比MAML取得了更优的结果。本文的理论分析部分值得一看。

算法

MAML求解的问题形式化的表示为

$$\underset{\varphi }{\min }{\mathbb{E}}_{\mathcal{T}}[{\mathcal{L}}_{\mathcal{T}}(U_{\mathcal{T}}^{(k)}(\varphi ))]$$

其中 $U_{\mathcal{T}}^{(k)}$ 表示使用任务 $\mathcal{T}$ 中采样的数据对模型初始化参数 $\varphi$ 更新了 k 次之后的结果。对于MAML算法来说，求解的问题简化为如下的形式

$$\underset{\varphi }{\min }{\mathbb{E}}_{\mathcal{T}}[{\mathcal{L}}_{\mathcal{T},\text{test}}(U_{\mathcal{T},\text{train}}(\varphi ))]$$

MAML算法求得的梯度下降的梯度为

$$\begin{gathered} {g}_{\text{MAML}}=\frac{\partial }{\partial \varphi }{\mathcal{L}}_{\mathcal{T},\text{test}}(U_{\mathcal{T},\text{train}}(\varphi ))=U_{\mathcal{T},\text{train}}^{\prime }(\varphi ){\mathcal{L}}_{\mathcal{T},\text{test}}^{\prime }(\varphi ) \\ \text{where }\varphi =U_{\mathcal{T},\text{train}}(\varphi ) \end{gathered}$$

对于FOMAML，有 $U_{\mathcal{T},\text{train}}^{\prime }(\varphi )=1$

Reptitle 算法则使用了不止一步SGD的一阶梯度结果对原问题进行求解，算法如下

一张直观的理解Reptile算法的图如下所示

多任务并行版本的更新公式如下所示

$$\varphi \leftarrow \varphi +\frac{ϵ}{n}\sum _{i=1}^n({\varphi }_i-\varphi )$$

理论分析

作者从两个角度给出了Reptitle生效的理论解释

Leading Order Expansion of the Update

假定对于训练中的一个任务 $\mathcal{T}$，梯度下降 k 次的过程中损失函数分别定义为 ${\mathcal{L}}_1...{\mathcal{L}}_k$，给出如下定义

对 $g_i$ 进行Taylor展开到 $O({\alpha }^2)$

考虑MAML算法的梯度，其中 $U_i(\varphi )=\varphi -\alpha L_i^{\prime }(\varphi )$，因此有

简化考虑，假设 $k=2$ ，有下式

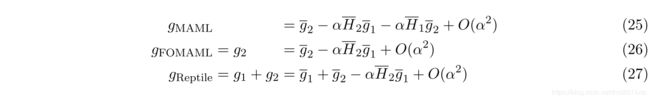
对梯度 $g$ 求期望，可以将式子中的每项的期望分为两种

• AvgGrad : $\text{AvgGrad}={\mathbb{E}}_{\mathcal{T},1}[{\overline{g}}_1]={\mathbb{E}}_{\mathcal{T},2}[{\overline{g}}_2]$
  (-AvgGrad) 的方向指向初始化参数 $\varphi$ 向联合训练问题的最小值。
• AvgGradInner :
  $$\begin{gathered} \text{AvgGradInner}={\mathbb{E}}_{\mathcal{T},1,2}[{\overline{H}}_1{\overline{g}}_2]={\mathbb{E}}_{\mathcal{T},1,2}[{\overline{H}}_2{\overline{g}}_1]=\frac{1}{2}{\mathbb{E}}_{\mathcal{T},1,2}[{\overline{H}}_2{\overline{g}}_1+{\overline{H}}_1{\overline{g}}_2] \\ =\frac{1}{2}{\mathbb{E}}_{\mathcal{T},1,2}[\frac{\partial }{\partial {\varphi }_1}({\overline{g}}_1\cdot {\overline{g}}_2)] \end{gathered}$$
  (-AvgGradInner) 的方向是增加给定任务的不同mini-batch的梯度之间的内积，从而提高泛化的方向。

因此，在 $k=2$ 的前提下，有

扩展到 $k$ 的场景

Finding a Point Near All Solution Manifolds

作者认为，Reptile 聚合得到的解在欧式空间内接近每一个任务的最优解的流形。假设 ${\mathcal{W}}_{\mathcal{T}}$ 表示任务 $\mathcal{T}$ 的最优参数，我们希望找到 $\varphi$ 使得距离每个最优解的流形的期望最小，即

$$\underset{\varphi }{\min }{\mathbb{E}}_{\mathcal{T}}[\frac{1}{2}D(\varphi ,{\mathcal{W}}_{\mathcal{T}}{)}^2]$$

作者试图证明Reptitle近似相当于在该优化目标上进行SGD算法。

给定非病态集合 $S\subset {\mathbb{R}}^d$，几乎对于所有的 $\varphi \in {\mathbb{R}}^d$，平方距离 $D(\varphi ,S{)}^2$ 的梯度是 $2(\varphi -P_S(\varphi ))$，$P_S(\varphi )$ 表示 $S$ 上离 $\varphi$ 最近的点，因此有

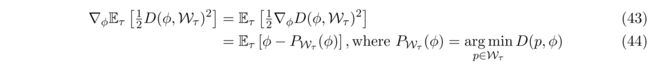
Reptile可以理解为每次从任务分布中抽样，进行SGD更新

实际上，我们不能精确地计算 $P_{{\mathcal{W}}_{\tau }}(\varphi )$ ，它被定义为 $L_{\tau }$ 的最小值。 但是，我们可以使用梯度下降来部分最小化这种损失。

实验

2-step Reptile明显比 2-step FOMAML差，这可以用2-step Reptile 相对于AvgGrad减轻了AvgGradInner权重的事实来解释（公式(34)和(35)）。 最重要的是，随着小批量的增加，所有方法都得到了改进。 当使用所有梯度的总和Reptile算法而不是仅使用最终梯度的FOMAML算法时，这种改进更为显着。

作者还探讨了算法对内循环超参数 mini-batch 的敏感性，并说明了如果错误地选择了mini-batch，则FOMAML的性能将显着下降。

实验着眼于shared-tail FOMAML与 seperate-tail FOMAML之间的区别，在 shared-tail FOMAML中，最终的内循环 mini-batch 与之前的内循环mini-batch 来自相同的数据分布（将任务数据划分为训练集和测试集）；seperate-tail FOMAML 中最终mini-batch 来自一组不相交的数据。确实，我们发现，分开尾的FOMAML比分享尾的FOMAML好得多。当用于计算元梯度的数据 $g_{\text{FOMAML}}=g_k$ 与早期训练的 mini-batch 明显重叠时，shared-tail FOMAML的性能会降低；但是，Reptile和seperate-tail FOMAML保持性能，并且对内循环超参数不是很敏感。

以上发现有几种可能的解释。一个假设是，shared-tail FOMAML的性能较差，因为在样本上执行几个内循环步骤后，该样本的损失梯度并未包含有关该样本的非常有用的信息。 换句话说，最初的几个SGD步骤可能会使模型接近局部最优值，然后进一步的SGD步骤可能会在该局部最优值附近反弹。

总结

作者提出了几个改进的方向

• 了解SGD在多大程度上可以自动优化泛化，以及是否可以在非元学习任务中放大此效果
• 在强化学习设置中应用Reptile
• 探索是否可以通过为分类器使用更深层次的体系结构来提高Reptile的少样本学习性能
• 探索正则化是否可以提高少样本学习性能，因为当前训练和测试错误之间存在很大差距
• 在少样本密度模型上评估Reptile