离散型随机变量,二项分布,泊松分布,几何分布(概统2.知识)
离散型随机变量,二项分布,泊松分布,指数分布,几何分布(概统2.知识)
1.0-1分布 。例如抛硬币,正面朝上设为1,反面朝上设为0
分布律为
| 结果随机变量X | 1 | 0 |
|---|---|---|
| 概率 P | p | 1-p |
2.二项分布
例如n次射击,每次只有射中与射不中两种结果,求n次射击恰好射中k次的概率。
设射中次数为随机数X,
二项分布就是独立事件n重伯努利试验,每次试验只有A发生与不发生两种结果,求n次试验中恰好发生k次的概率。
伯努利概型在前面博文已经写过,请参看前面博文:独立性,重复独立事件,伯努利概型(概统1)
P{X=k} = $C_{n}{k}p{k}q^{n-k}, $k=0,1,2,…n
q=1-p;
记为 X~B(n,p)
二项分布的最大k值问题,请看博文:计算二项分布最大值,二项分布推导泊松分布,几何分布(概统2.证明)
3.泊松分布
由前面二项分布,当n趋于无穷大,p又趋于0时,可以由二项分布推导出泊松分布。
3.1)泊松分布第一种:单位时间内发生的次数是常数,事件按固定的时间频率发生
为什么具有单位时间内平均发生次数特点的事件可以看做泊松分布? 、
理解方式:可以将”单位时间“无限分割,这样n等分就无限多,每个等分就无限小,无限小的时间事件发生的概率趋向于0,于是这就是一个{ n → ∞ , p → 0 n\to\infty, p\to0 n→∞,p→0}
的问题,同时,n*p=单位时间平均发生次数= λ \lambda λ
例如, 某医院平均每小时出生3个婴儿,接下来1小时,至少出生2个婴儿的概率是多少?
设随机变量为X
P {X=k} = ( λ t ) k k ! e − λ t \frac{(\lambda t)^{k} }{k!} e^{-\lambda t} k!(λt)ke−λt, k=0,1,2,…
其中 λ \lambda λ表示单位时间内,发生结果的平均次数。
X为随机变量,k表示t时间内发生结果的次数。
所以上面公式的意思就是:已知单位时间内,
发生结果的平均次数为 λ \lambda λ(如每小时出生3个婴儿),
求t时间内(t小时内),发生k次结果的概率(出生k个婴儿的概率)。
随机变量X代表出生婴儿的个数,P {X=k} 代表出生k个婴儿的概率,
λ \lambda λ为已知数,代表平均单位时间出生婴儿的个数。
求t时间内出生k个婴儿的概率:P {X=k} ,
直观理解,当然是单位时间出生 λ \lambda λ个婴儿的概率最大。
t是单位时间的倍数,如果t取1,公式就变成:
P {X=k} = ( λ ) k k ! e − λ \frac{(\lambda )^{k} }{k!} e^{-\lambda } k!(λ)ke−λ, k=0,1,2,…
称X为服从参数为 λ \lambda λ的泊松分布,记为 X~$\pi (\lambda ) $ ,或者 X~$P(\lambda ) $
[例题3.1] - 某医院平均每小时出生3个婴儿,
1)) 接下来2小时,一个婴儿都不出生的概率是多少?
2)) 接下来1小时,至少出生2个婴儿的概率是多少?
3)) 接下来的15到30分钟,会有婴儿出生的概率是多少?
解:
1)) 满足事件按固定时间频率发生的条件。
P {X=k} = ( λ t ) k k ! e − λ t \frac{(\lambda t)^{k} }{k!} e^{-\lambda t} k!(λt)ke−λt, k=0,1,2,…
接下来2小时:t=2
λ \lambda λ=发生频率=3,
一个婴儿都不出生:k=0,
P {X=0,t=2} = ( 3 ∗ 2 ) 0 0 ! e − 3 ∗ 2 \frac{(3*2 )^{0} }{0!} e^{-3*2} 0!(3∗2)0e−3∗2 = e − 6 ≈ e^{-6} \approx e−6≈ 0.0025 = 0.25% ;
所以说,接下来2小时,一个婴儿都不出生的概率不到1%;
2)) 接下来1小时:t=1
λ \lambda λ=发生频率=3,
P{X>=2,t=1}=1-P{X=0,t=1}-P{X=1,t=1};
P{X=0,t=1} = ( 3 ∗ 1 ) 0 0 ! e − 3 ∗ 1 \frac{(3* 1)^{0} }{0!} e^{-3* 1} 0!(3∗1)0e−3∗1 = e − 3 e^{-3} e−3;
P{X=1,t=1} = ( 3 ∗ 1 ) 1 1 ! e − 3 ∗ 1 \frac{(3* 1)^{1} }{1!} e^{-3* 1} 1!(3∗1)1e−3∗1 = 3 e − 3 3e^{-3} 3e−3;
P{X>=2,t=1}=1-P{X=0,t=1}-P{X=1,t=1} = 1 − e − 3 − 3 e 3 = 1 − 4 ∗ e − 3 1-e^{-3}-3e^{3} =1 - 4*e^{-3} 1−e−3−3e3=1−4∗e−3
≈ 0.8009 ≈ 80 \approx 0.8009 \approx 80% ≈0.8009≈80
所以说接下来1小时,很大概率至少出生2个婴儿 。因为平均每小时出生3个婴儿,因此,接下来1小时里,最有可能发生的概率就是平均概率(就等于 λ \lambda λ),也印证了后面一个问题:在泊松分布中,k取 λ \lambda λ时,P{X=k}有最大值。
3)) 接下来的15到30分钟,会有婴儿出生的概率是多少?
有婴儿出生的概率=有1个到无限个的概率 ,用它的反面来计算,
有1个到无限个的概率 = 1 - 有0个出生的概率
P{X>=1} = 1 - P{X=0}
因为t的单位是小时,15分钟换算成小时=0.25小时,30分钟换算成小时=0.5小时
P{X=0,t=0.25} = ( 3 ∗ 0.25 ) 0 0 ! e − 3 ∗ 0.25 \frac{(3* 0.25)^{0} }{0!} e^{-3* 0.25} 0!(3∗0.25)0e−3∗0.25 = e − 3 ∗ 0.25 e^{-3* 0.25} e−3∗0.25 ;
P{X=0,t=0.50} = ( 3 ∗ 0.50 ) 0 0 ! e − 3 ∗ 0.50 \frac{(3* 0.50)^{0} }{0!} e^{-3* 0.50} 0!(3∗0.50)0e−3∗0.50 = e − 3 ∗ 0.50 e^{-3* 0.50} e−3∗0.50 ;
P{X>=1,t=0.25} = 1 - P{X=0,t=0.25} = 1 - e − 0.75 e^{-0.75} e−0.75 ;
P{X>=1,t=0.50} = 1 - P{X=0,t=0.50} = 1 - e − 1.5 e^{-1.5} e−1.5 ;
接下来的15到30分钟的时间段的概率=Px
=P(X>=1,t=0.5) - P(X>=1,t=0.25) = e − 0.75 − e − 1.5 e^{-0.75} - e^{-1.5} e−0.75−e−1.5 = 0.2492%
3.2)泊松分布第二种:大数据样本,样本总数N很大,每个个体发生的概率p很小,N*p是一个常数,等于一段时间内平均总体发生次数
N*p = λ \lambda λ,N是个体数目,样本总数,p是每个个体发生的概率,每个个体发生的概率很小,比如机器故障,汽车路过路口时发生故障, λ \lambda λ就是一定时间内发生的总平均概率。
例如, 交通路口,高峰时段有1000辆车路过路口,每辆车出故障的概率为0.001 。
这些类型的实例是n很大,p很小,n*p等于一个常数,因此可以用泊松分布。
P {X=k} = ( λ ) k k ! e − λ \frac{(\lambda )^{k} }{k!} e^{-\lambda } k!(λ)ke−λ, k=0,1,2,…
称X为服从参数为 λ \lambda λ的泊松分布,记为 X~$\pi (\lambda ) $ ,或者 X~$P(\lambda ) $
[例题3.2] 某交通路口,高峰时段有1000辆车路过路口,每辆车出故障的概率为0.0001,
1)) 求发生事故的概率分布。
2)) 求某段时间内同时发生两次以上事故的概率是多少?
解:
1)) 此题 n =1000, p=0.0001, np=0.1
符合n很大,p趋于0,np= λ \lambda λ ,所以X服从泊松分布
发生事故的概率分布律为
P{X=k} = λ k k ! ∗ e − λ \frac{\lambda^k}{k!} * e^{-\lambda} k!λk∗e−λ = 0. 1 k k ! ∗ e − 0.1 \frac{0.1^k}{k!} * e^{-0.1} k!0.1k∗e−0.1
2)) 某一段时间内发生两次以上的事故的概率,为两次到无限次的概率之和,
用减去0次和1次计算。
P{X>=2}=1-P{X=0}-P{X=1}
= 1 - 0. 1 0 0 ! ∗ e − 0.1 \frac{0.1^0}{0!} * e^{-0.1} 0!0.10∗e−0.1 - 0. 1 1 1 ! ∗ e − 0.1 \frac{0.1^1}{1!} * e^{-0.1} 1!0.11∗e−0.1
= 1 - 1.1 ∗ e 0 . 1 1.1*e^0.1 1.1∗e0.1 = 0.0045
3.3)总结泊松分布适用情形,泊松分布的特征
泊松分布可看作是单位时间、单位面积或单位容积中颗粒数或某罕见事件发生数的概率分布
泊松分布的特征,见【概率论与数理统计.2.随机变量。应用】-- 泊松分布的特征与应用
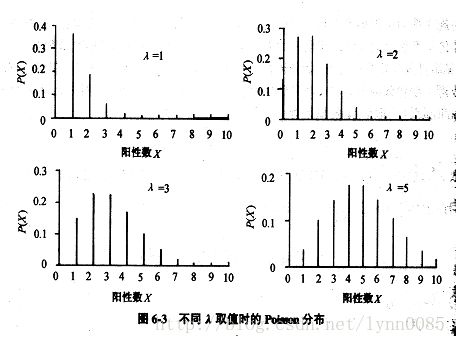
泊松分布的图形示意
由图形看出,泊松分布的特征:
1))泊松分布的图形只取决于平均数 λ \lambda λ
2))当 λ \lambda λ很小时,图形是很偏的,但当 λ \lambda λ增大时,图形逐渐趋向正态,当 λ \lambda λ=20时,泊松分布接近正态,当 λ \lambda λ>50时,可以认为是正态分布。
3))由泊松分布的图形示例,可以看得出来,k值在 λ \lambda λ附近时,概率最大,
即 k = λ k=\lambda k=λ,P{X=k}等于峰值**
3.4 )泊松分布公式与 自然数 的定义 e
参考前面博文【基础数学】–对自然数e的理解,e的证明,e的计算
e x e^{x} ex = ∑ i = 0 ∞ ( x ) i i ! \sum_{i=0}^{\infty}\frac{(x)^{i}}{i!} ∑i=0∞i!(x)i
e x e^{x} ex = 1+x+ ( x ) 2 2 ! + ( x ) 3 3 ! + . . . + ( x ) n 1 n ! \frac{(x)^2}{2!}+\frac{(x)^3}{3!} + ... +(x)^{n}\frac{1}{n!} 2!(x)2+3!(x)3+...+(x)nn!1
===
近似计算(e<4)的情况,e的指数越大,后面的项越大,越需要多项展开):
e x e^{x} ex = 1+x+$\frac{(x)2}{2}+\frac{(x)3}{6} + \frac{(x)^4}{24} +\frac{(x)^5}{120} $=====
思考问题:
e x e^{x} ex的泰勒级数展开多项式中,哪一项的值最大?
答案是:x等于多少就是哪项值最大,恰好第x项的值最大。
可以参考前面博文对自然数e的理解,e的证明,e的计算(基础)
物理意义:单位时间内事件发生的次数最大可能性就是平均概率。
===
比如x=1,第一项最大 x=1。
x=2: 第一项及第二项 都是最大 ( x ) 2 2 = 2 2 2 = 2 \frac{(x)^2}{2}=\frac{2^2}{2}=2 2(x)2=222=2;
x=3,第三项 最大 ( x ) 3 6 = 3 3 6 \frac{(x)^3}{6}=\frac{3^3}{6} 6(x)3=633=4.73;
x=4,第四项 最大 ( x ) 4 24 = 4 4 24 = 256 24 \frac{(x)^4}{24}=\frac{4^4}{24}=\frac{256}{24} 24(x)4=2444=24256=12;
以此类推…
可以看到 λ k k ! \frac{\lambda^{k} }{k!} k!λk 其实就是 e λ e^{\lambda} eλ 的第k项。
也就是等于说,P{X=k}的概率,就是 e λ e^{\lambda} eλ 的第k项 的占比例。
泊松分布,P{X=k}的值,就是 e λ e^{\lambda} eλ 的第k项 的占比例, 那么 k=?时,P{X=k}最大? 从定义上说, λ {\lambda} λ 表示单位时间发生次数的平均数,或者表示 N*p 总共发生故障数。
从直观上理解,单位时间最有可能发生的次数当然是平均数,也就是 k = λ {\lambda} λ 时, P{X= λ {\lambda} λ} 取得最大值。
4.指数分布
网上所介绍的指数分布的引出,也是从泊松分布引申而来的,可以看做是泊松分布的特殊形态, 就是令X=0,事件一个都不发生,求P{N(t)}的分布
即: "求事件发生的时间间隔”
P{X=0, N(t)} = ( λ t ) 0 0 ! ∗ e − λ t = e − λ t \frac{(\lambda t)^0}{0!} * e^{-\lambda t} = e^{-\lambda t} 0!(λt)0∗e−λt=e−λt
”在t 时间内出现一个以上的概率“
P{X>0, N(t)} = $1 - e^{-\lambda t} $;
比如前面的[例题3.1] ,关注第3))个问题,
3)) 接下来的15到30分钟,会有婴儿出生的概率是多少?
P{X>=1, 0.25< t<= 0.50} = (1- e − 1.5 e^{-1.5} e−1.5) - (1 - e − 0.7.5 e^{-0.7.5} e−0.7.5) =
e − 0.7.5 e^{-0.7.5} e−0.7.5 - e − 1.5 e^{-1.5} e−1.5 = 0.2492%
- 泊松分布关注的问题是:t 时间内,发生k次的概率分布
P{X=k, N(t)} = ( λ t ) k k ! ∗ e − λ t \frac{(\lambda t)^k}{k!} * e^{-\lambda t} k!(λt)k∗e−λt
=== - 指数分布是泊松分布X=0的特殊项,关注的问题是: 事件发生的时间间隔
P{X=0, N(t)} = ( λ t ) 0 0 ! ∗ e − λ t = e − λ t \frac{(\lambda t)^0}{0!} * e^{-\lambda t} = e^{-\lambda t} 0!(λt)0∗e−λt=e−λt
或者:在t 时间内,出现一个以上的概率
P{X>0, N(t)} = $1 - e^{-\lambda t} $;
5.几何分布
几何分布也是从二项分布引申而来。实际背景是重复独立试验下首次成功的概率(n重伯努利试验,首次成功的 n 值)
举例:射击n次,首次射中时的n值。
有放回地抽取样品,首次抽到次品时的抽取次数。
几何分布公式(事件首次发生的n值分布):
P{X=n} = p ( 1 − p ) n − 1 p(1-p)^{n-1} p(1−p)n−1 ;
纪为 X~G§
二项分布到几何分布的推导见二项分布最大值,推导出泊松分布,几何分布((概统2.证明)