图(Graph):是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
线性表中我们把元素叫元素,树中叫结点,在途中数据元素我们则称为顶点(Vertex)。
线性表可以没有数据元素,称为空表,树中可以没有结点,叫空树,图中强调顶点集合V要有穷且非空。
有向边:若从顶点Vi到Vj的边有方向,则称这条边为有向边,也称为弧(Arc),用有序偶
简单图:在图结构中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
无向完全图:在无向图中,如果任意两个顶点间都存在边,则称该图为无向图。含有n个顶点的无向完全图有n*(n-1)/2条边。
有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边。
稀疏图和稠密图:这里的稀疏图和稠密图是模糊的概念,都是相对而言的,通常认为边或弧数小于n*logn(n是顶点个数)的图称为稀疏图,反之称为稠密图。
带权的图通常称为网(Network):图的边或弧带有与它相关的数字,这种与图的边或弧相关的树叫权(Weight)。
假设有两个图G1=(V1,E1)和G2=(V2,E2),如果V2⊆V1,E2⊆E1,则称G2为G1的子图(Subgraph)。
对于无向图G=(V,E),如果边(V1,V2)∈E,则称顶点V1和V2互为邻接点(Adjacent),即V1和V2相邻。边(V1,V2)依附(incident)于顶点V1和V2,或者说边(V1,V2)与顶点V1和V2相关联。
顶点V的度(Degree)是和V相关联的边的数目,记为TD(V)。
路径的长度是路径上的边或弧的数目。
第一个顶点到最后一个顶点相同的路径称为回路或环(Cycle)。
序列中顶点不重复出现的路径叫简单路径,除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路,称为简单回路或简单环。
图的遍历:
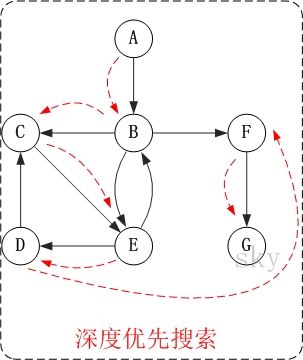
深度优先搜索:假设初始状态是图中所有顶点未曾被访问,则深度优先搜索可从图中某个顶点发v 出发,访问此顶点,然后依次从v 的未被访问的邻接点出发深度优先遍历图,直至图中所有和v 有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
广度优先搜索:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
这是我推荐的图的遍历的博客:https://www.cnblogs.com/skywang12345/p/3711483.html
这周我打算开始复习前面的内容,巩固一下已经遗忘的知识。