Step1：模型 16个相机参数（内参、外参、畸变参数）

16个相机参数

摘要：本文首先介绍了针孔相机模型，然后推导四个坐标轴变换的关系，引出R、T、K、D中包含相机的5个内参，6个外参，5个畸变参数。相机的标定是从空间点及其对应的像素点，获得相机的位置信息和内部参数信息的过程，16个相机参数的总结为此提供了模型基础。

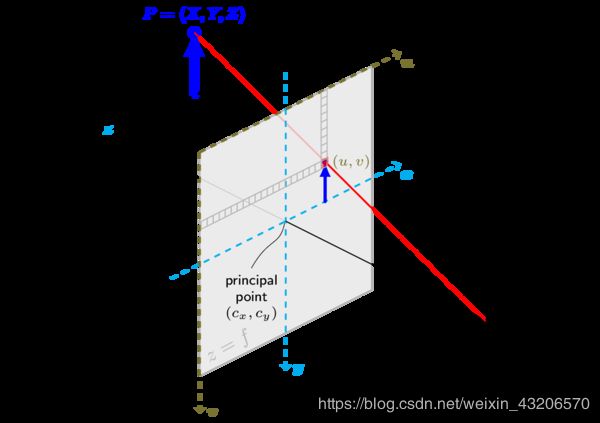
一、针孔相机模型

相机中有四个坐标系，分别为{world}，{camera}，{image}，{pixel}

• {world}为世界坐标系，可以任意指定$x_w$轴和$y_w$轴
• {camera}为相机坐标系，原点位于小孔，z轴与光轴重合，$x_c$轴和$y_c$轴平行投影面
• {image}为图像坐标系，原点位于光轴和投影面的交点，$x_p$轴和$y_p$轴平行投影面
• {pixel}为像素坐标系，从小孔向投影面方向看，投影面的左上角为原点$O_p$${}_i$${}_x$，uv轴和投影面两边重合

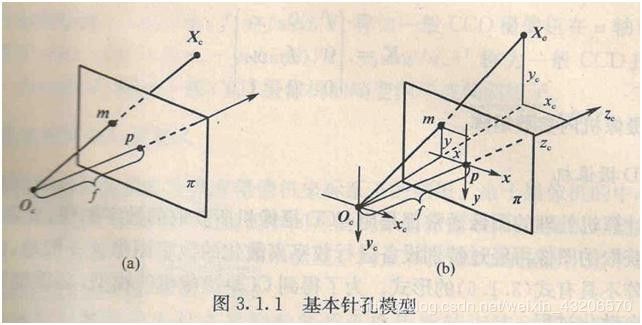
图片说明：{camera}：O${}_c$-x${}_c$y${}_c$z${}_c$，相机中心点Oc，焦距f。{picture}：O-xy，像平面π。主轴：从$O_c$出发，垂直于像平面的射线 。主点：主轴与像平面的交点p。

二、四个坐标轴的变换关系

介绍如何从世界坐标轴，通过相机坐标轴和像面坐标轴，得到像素坐标轴的变换的过程，即$world:P_w=(x_w,y_w,z_w{)}^T$----->$camera:P_c=(x_c,y_c,z_c{)}^T$------>$image:m=(x_p,y_p,1{)}^T$----->$pixel:Pix=(u,v,1{)}^T$

2.1 从{world}到{camera}

设某点在{world}中的坐标为$Pw=(x_w,y_w,z_w{)}^T$，在{camera}中的坐标为$Pc=(x_c,y_c,z_c{)}^T$。则
$$P_c=\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]P_w$$
其中，R为正交旋转矩阵，
$$R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$
T为平移矩阵，$$T={\left[\begin{array}{ccc}{t}_x& t_y& t_z\end{array}\right]}^T$$

2.2 从{camera}到{image}

设空间点$X_c$在{camera}下：$P_c=(xc,yc,zc,1{)}^T$，其像点m在{image}的齐次坐标为$m=(x_p,y_p,1{)}^T$。由图中相似三角形可得，
$$\{\begin{array}{c}{x}_p=\frac{f{x}_c}{z_c}\\ \\ y_p=\frac{f{y}_c}{z_c}\end{array}$$
写成矩阵表示为，
$$z_{c}m=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]P_c$$
实际中，主点可能不在图像坐标系原点，若主点在图像坐标系中的坐标为$$p=(x_0,y_0,1{)}^T$$
则
$$z_{c}m=\left[\begin{array}{c}fx\\ fy\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& x_0& 0\\ 0& f& y_0& 0\\ 0& 0& 1& 0\end{array}\right]P_c$$

2.3 从{image}到{pixel}

假设一个像素的长和宽分别为dx，dy，设像素坐标$Pix=(u,v,1{)}^T$，则
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}1/d_x& 0& 0\\ 0& 1/d_y& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_p\\ y_p\\ 1\end{array}\right]$$
结合{camera}到{image}的变换，则{camera}到{pixel}的变换矩阵K为
$$K=\left[\begin{array}{ccc}1/d_x& 0& 0\\ 0& 1/d_y& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}f& 0& x_0\\ 0& f& y_0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]$$
其中，$f_x=f/dx$,$f_y=f/dy$,称为相机在u轴和v轴方向上的尺度因子。
相机主点为$(u_0，v_0{)}^T=(x_0/dx，y_0/dy{)}^T$

2.4 综合：从{world}到{pixel}

四个坐标系的变换过程：$world:P_w=(x_w,y_w,z_w{)}^T$----->$camera:P_c=(x_c,y_c,z_c{)}^T$----->$image:m=(x_p,y_p,1{)}^T$----->$pixel:Pix=(u,v,1{)}^T$，
矩阵表示为：
$$z_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K\cdot \left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$$

2.5 畸变参数

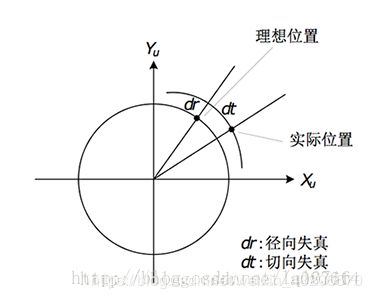
2.5.1 径向畸变

径向畸变（桶形畸变和枕形畸变）产生原因：光线在远离透镜中心的地方偏折更大。矫正公式：
$$x_{corrected}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$$$y_{corrected}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$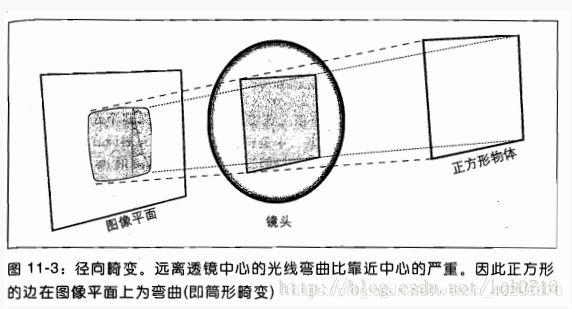

2.5.2 切向畸变

切向畸变产生原因：透镜不完全平行于图像平面。矫正公式：
$$x_{corrected}=x+[2p_{1}xy+p_2(r^2+2x^2)]$$$$y_{corrected}=y+[p_1(r^2+2y^2)+2p_{2}xy]$$
由此得到相机的5个畸变参数：$D（k_1,k_2,k_3,p_1,p_2）$

2.6 小结

综上，16个单目相机的参数：

• 10个内部参数（只与相机有关）：
  • 5个内部矩阵参数K：$f$,$dx$,$dy$,$u_0$,$v_0$
    （也可视作4个参数$f_x$,$f_y$,$u_0$,$v_0$）
  • 5个畸变参数D：$k_1,k_2,k_3,p_1,p_2$
• 6个外部参数（取决于相机在{world}的位置）：
  • 3个旋转参数R
  • 3个平移参数T

推导：

1.【旋转矩阵】https://www.cnblogs.com/caster99/p/4703033.html
旋转矩阵是一个完美的矩阵——正交矩阵。它的行列式为1，且每个列向量都是单位向量且相互正交，它的逆等于它的转置。
2.【平移矩阵】http://frankorz.com/2017/09/24/matrix-transformation-2/ 平移矩阵，比较平移旋转及旋转平移，说明先旋转后平移的好处
3.【反射矩阵推导】https://www.cnblogs.com/wantnon/p/5630915.html
4.【相机畸变详细推导 】https://blog.csdn.net/waeceo/article/details/51024396
5.【6个参数 旋转平移下坐标变换】https://blog.csdn.net/xuelabizp/article/details/50314633

参考：

1.https://blog.csdn.net/xuelabizp/article/details/50314633
2.https://blog.csdn.net/u010128736/article/details/52850444
3.https://www.cnblogs.com/Jessica-jie/p/6596450.html?tdsourcetag=s_pctim_aiomsg
4.https://blog.csdn.net/yangdashi888/article/details/51356385
5.https://blog.csdn.net/a083614/article/details/78579163
6.https://blog.csdn.net/lql0716/article/details/71973318?locationNum=8&fps=1）