VINS-Mono关键知识点总结——边缘化marginalization理论和代码详解

VINS-Mono关键知识点总结——边缘化marginalization理论和代码详解

个人觉得整个VINS最难理解的部分就是边缘化（marginalization），除去理论学习，仅仅看代码前前后后就花了好几天，也并没有全部看懂，这里尽可能地对这部分只是详细总结下

1. 边缘化理论

边缘化相关的理论主要是参考高博和贺博的课程以及三篇参考文献：
《The Humble Gaussian Distribution》
《Exactly Sparse Extended Information Filters for Feature-Based SLAM》
《Consistency Analysis for Sliding-Window Visual Odometry》

1.1 为什么要进行边缘化操作？

首先我们知道，如果仅仅从前后两帧图像来计算相机变换位姿， 其速度快但是精度低，而如果采用全局优化的方法（比如Bundle Adjustment），其精度高但是效率低，因此前辈们引入了滑窗法这样一个方法，每次对固定数量的帧进行优化操作，这样既保证了精度又保证了效率。既然是滑窗，在滑动的过程中必然会有新的图像帧进来以及旧的图像帧离开，所谓边缘化就是为了使得离开的图像帧得到很好的利用。

1.2 怎样进行边缘化呢？

我们根据运动模型和观测模型建立$H$矩阵（高斯牛顿法中的$J{J}^T$）的过程其实就是根据概率图模型（多元高斯分布）建立各个节点变量间的信息矩阵（协方差矩阵的逆）的过程，而边缘化则是去掉概率图中的某一个节点后信息矩阵会发生怎样的变换的问题。如下图

其中$$\begin{array}{rl}{x}_2& =v_2\\ x_1& =w_1{x}_2+v_1\\ x_3& =w_3{x}_2+v_3\end{array}$$其中$v_i$相互独立，且各自服从协方差为${\sigma }_i^2$的高斯分布，可以求得上面概率图模型的信息矩阵为（求解过程成省略）$$\mathbf{\Lambda }={\mathbf{\Sigma }}^{-1}=\left[\begin{array}{ccc}\frac{1}{{\sigma }_1^2}& -\frac{w_1}{{\sigma }_1^2}& 0\\ -\frac{w_1}{{\sigma }_1^2}& \frac{w_1^2}{{\sigma }_1^2}+\frac{1}{{\sigma }_2^2}+\frac{w_3^2}{{\sigma }_1^2}& -\frac{w_3}{{\sigma }_2^2}\\ 0& -\frac{w_3}{{\sigma }_3^2}& \frac{1}{{\sigma }_3^2}\end{array}\right]$$边缘化问题是假如我们将$x_3$去掉之后，概率图模型的信息矩阵会发生怎样的变化，如下图所示：

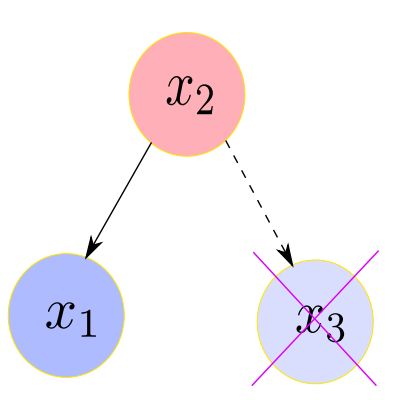
我们先不加证明的给出结论为：$${\mathbf{\Sigma }}_2^{-1}=\left[\begin{array}{cc}\frac{1}{{\sigma }_1^2}& -\frac{w_1}{{\sigma }_1^2}\\ -\frac{w_1}{{\sigma }_1^2}& \frac{w_1^2}{{\sigma }_1^2}+\frac{1}{{\sigma }_2^2}\end{array}\right]$$下面开始证明，现在假设$a,b$两个高斯分布的变量之间的协方差矩阵为：$$\mathbf{K}=\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]$$其中$A=\mathrm{cov}(a,a),D=\mathrm{cov}(b,b),C=\mathrm{cov}(a,b)$，那么其联合分布可以表示为边际分布和条件部分的乘积如下：$$P(a,b)=P(a)P(b|a)\propto \exp \left(-\frac{1}{2}{\left[\begin{array}{l}a\\ b\end{array}\right]}^{\top }{\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]}^{-1}\left[\begin{array}{l}a\\ b\end{array}\right]\right)$$然后对高斯分布进行分解可以直接求的边际分布$P(a)$和条件分布$P(b|a)$的表达形式，如下：$$\begin{array}{l}P(a,b)\\ \propto \exp \left(-\frac{1}{2}{\left[\begin{array}{c}a\\ b\end{array}\right]}^{\top }{\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]}^{-1}{\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]}^{-1}\left[\begin{array}{c}A\\ b\end{array}\right]\right)\\ \propto \exp \left(-\frac{1}{2}{\left[\begin{array}{c}a\\ b\end{array}\right]}^{\top }\left[\begin{array}{cc}I& -A^{-1}{C}^{\top }\\ 0& I\end{array}\right]\left[\begin{array}{cc}{A}^{-1}& 0\\ 0& {\Delta }_{\mathrm{A}}^{-1}\end{array}\right]\left[\begin{array}{cc}I& 0\\ -C{A}^{-1}& I\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]\right)\\ \propto \exp \left(-\frac{1}{2}\left[a^{\top }{\left(b-C{A}^{-1}a\right)}^{\top }\right]\left[\begin{array}{cc}{A}^{-1}& 0\\ 0& {\Delta }_{\mathrm{A}}^{-1}\end{array}\right]\left[\begin{array}{c}a\\ b-C{A}^{-1}a\end{array}\right]\right)\\ \propto \exp \left(-\frac{1}{2}\left(a^{\top }{A}^{-1}a\right)+{\left(b-C{A}^{-1}a\right)}^{\top }{\Delta }_{\mathrm{A}}^{-1}\left(b-C{A}^{-1}a\right)\right)\\ \propto \exp \left(-\frac{1}{2}{a}^{\top }{A}^{-1}a\right)\exp \left(-\frac{1}{2}{\left(b-C{A}^{-1}a\right)}^{\top }{\Delta }_{\mathrm{A}}^{-1}\left(b-C{A}^{-1}a\right)\right)\end{array}$$其中$$P(a)\propto \exp \left(-\frac{1}{2}{a}^{\top }{A}^{-1}a\right)$$$$P(b|a)\propto \exp \left(-\frac{1}{2}{\left(b-C{A}^{-1}a\right)}^{\top }{\Delta }_{\mathrm{A}}^{-1}\left(b-C{A}^{-1}a\right)\right)$$则$$P(a)\sim \mathcal{N}(0,A)\text{\hspace{1em}(1)}$$$$P(b|a)\sim \mathcal{N}\left(C{A}^{-1}a,{\Delta }_A\right)\text{\hspace{1em}(2)}$$$P(a)$和$P(b|a)$的协方差矩阵分别是，$A$和${\Delta }_A$通过这个结论可以看出，从联合分布中的协方差矩阵求得边际概率的协方差矩阵$A$是简单的，求得条件概率的协方差矩阵${\Delta }_A$会相对复杂，但是呢，我们应该更加关注联合分布的信息矩阵，因为我们在BA问题中研究的其实是信息矩阵而不是协方差矩阵，假设我们已知上述问题的信息矩阵为：$${\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]}^{-1}=\left[\begin{array}{cc}{\Lambda }_{aa}& {\Lambda }_{ab}\\ {\Lambda }_{ba}& {\Lambda }_{bb}\end{array}\right]$$那么可以求得协方差矩阵各块和信息矩阵各块之间的关系为$${\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]}^{-1}=\left[\begin{array}{cc}{A}^{-1}+A^{-1}{C}^{\top }{\Delta }_{\mathrm{A}}^{-1}C{A}^{-1}& -A^{-1}{C}^{\top }{\Delta }_{\mathrm{A}}^{-1}\\ -{\Delta }_{\mathrm{A}}^{-1}C{A}^{-1}& {\Delta }_{\mathrm{A}}^{-1}\end{array}\right]\triangleq \left[\begin{array}{cc}{\Lambda }_{aa}& {\Lambda }_{ab}\\ {\Lambda }_{ba}& {\Lambda }_{bb}\end{array}\right]\text{\hspace{1em}(3)}$$由（1）我们知道$P(b|a)$的协方差矩阵为${\Delta }_A$，那么它的信息矩阵就是${\Delta }_A^{-1}$，由（3）就可以知道其信息矩阵为${\Lambda }_{bb}$，同理，由（2）和（3）我们可以知道$P(a)$的信息矩阵为${\Lambda }_{aa}-{\Lambda }_{ab}{\Lambda }_{bb}^{-1}{\Lambda }_{ba}$，由此我们就知道如何从联合分布的信息矩阵中求解$P(a)$和$P(b|a)$的信息矩阵了，这一点应用到我们上面最开始的问题中，已知联合分布的信息矩阵为$${\mathbf{\Sigma }}^{-1}=\left[\begin{array}{ccc}\frac{1}{{\sigma }_1^2}& -\frac{w_1}{{\sigma }_1^2}& \theta \\ -\frac{w_1}{{\sigma }_1^2}& \frac{w_1^2}{{\sigma }_1^2}+\frac{1}{{\sigma }_1^2}+\frac{w_3^2}{{\sigma }_1^2}& \frac{w_3}{{\sigma }_3^2}\\ \theta & \frac{w_3}{{\sigma }_3^2}& \frac{1}{{\sigma }_3^2}\end{array}\right]$$那么，其边际概率的信息矩阵${\mathbf{\Sigma }}_2^{-1}$为$$\begin{array}{rl}{\mathbf{\Sigma }}_2^{-1}& ={\Lambda }_{aa}-{\Lambda }_{ab}{\Lambda }_{bb}^{-1}{\Lambda }_{ba}\\ & ={\Lambda }_{aa}-\left[\begin{array}{c}0\\ -\frac{w_3}{{\sigma }_3^2}\end{array}\right]{\sigma }_3^2\left[0-\frac{w_3}{{\sigma }_3^2}\right]\\ & ={\Lambda }_{aa}-\left[\begin{array}{cc}0& 0\\ 0& \frac{w_3}{{\sigma }_3^2}\end{array}\right]\\ & =\left[\begin{array}{cc}\frac{1}{{\sigma }_1^2}& -\frac{w_1}{{\sigma }_1^2}\\ -\frac{w_1}{{\sigma }_1^2}& \frac{w_1^2}{{\sigma }_1^2}+\frac{1}{{\sigma }_2^2}\end{array}\right]\end{array}$$这样就证明了问题的结论，而这一步${\Lambda }_{aa}-{\Lambda }_{ab}{\Lambda }_{bb}^{-1}{\Lambda }_{ba}$我们称之为求Shur补的操作，我们将其应用到实际的更复杂中就是下面这种情况，下面这幅图很好地说明了边缘化的过程：

上图中，${\xi }_1$、${\xi }_2$、${\xi }_3$、${\xi }_4$、${\xi }_5$、${\xi }_6$分别为六个节点，通过边缘化操作可以将原稀疏的矩阵变成稠密矩阵，而增加的稠密部分其实就是被边缘化掉的那个节点传递给当前状态的信息，也就是使得原本独立的各个变量变得相关。

1.3 在实际的边缘化操作中有什么需要注意的吗？

一个比较值得注意的问题是新老信息融合的问题，也就是FEJ算法的使用，如下所示:

承接上面的例子，当我们边缘话掉变量${\xi }_1$有加入新的变量${\xi }_7$会有如下新老信息融合的情况发生，就${\xi }_2$这个矩阵而言，它的信息矩阵是有两部分构成的。

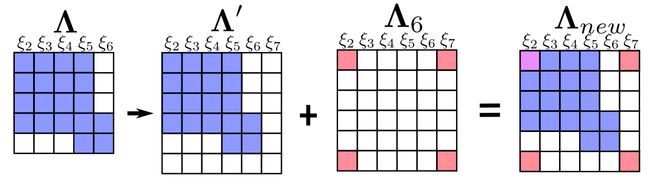
新老信息融合的问题在于旧的求解雅克比矩阵的变量线性化点和和新的求解雅克比矩阵的变量线性化点不同，可能会导致信息矩阵的零空间发生变化，使得不客观的变量变得可观，从而引入错误信息，这个解释可能会比较抽象，更加具体的解释可以参看贺博的博客SLAM中的marginalization 和 Schur complement，上述问题的解决办法呢就是FEJ算法：不同残差对同一个状态求雅克比时，线性化点必须一致。这样就能避免零空间退化而使得不可观变量变得可观，具体来说就是计算$r_{27}$ 对 ${\xi }_2$ 的雅克比时，${\xi }_2$ 的线性话点必须和 $r_{12}$对其求导时一致。

2. 代码剖析

上面理论搞清楚了其实只是第一步，由于VINS-mono优化的变量较多，VINS-mono的边缘化操作实际上要复杂很多，VINS-mono的边缘化相关代码在estimator.cpp的Estimator类的optimization()函数中，该函数先会先进行后端非线性优化然后紧接着就是边缘化操作，下面就针对这个函数中的边缘化相关代码进行剖析。

2.1 优化变量分析

首先我们确定下参与边缘化操作的变量有哪些，这个可以从vector2double()函数中看出来，因为ceres中变量必须用数组类型，所以需要这样一个函数进行数据类型转换，如下：

void Estimator::vector2double()
{
    for (int i = 0; i <= WINDOW_SIZE; i++)
    {
        para_Pose[i][0] = Ps[i].x();
        para_Pose[i][1] = Ps[i].y();
        para_Pose[i][2] = Ps[i].z();
        Quaterniond q{Rs[i]};
        para_Pose[i][3] = q.x();
        para_Pose[i][4] = q.y();
        para_Pose[i][5] = q.z();
        para_Pose[i][6] = q.w();

        para_SpeedBias[i][0] = Vs[i].x();
        para_SpeedBias[i][1] = Vs[i].y();
        para_SpeedBias[i][2] = Vs[i].z();

        para_SpeedBias[i][3] = Bas[i].x();
        para_SpeedBias[i][4] = Bas[i].y();
        para_SpeedBias[i][5] = Bas[i].z();

        para_SpeedBias[i][6] = Bgs[i].x();
        para_SpeedBias[i][7] = Bgs[i].y();
        para_SpeedBias[i][8] = Bgs[i].z();
    }
    for (int i = 0; i < NUM_OF_CAM; i++)
    {
        para_Ex_Pose[i][0] = tic[i].x();
        para_Ex_Pose[i][1] = tic[i].y();
        para_Ex_Pose[i][2] = tic[i].z();
        Quaterniond q{ric[i]};
        para_Ex_Pose[i][3] = q.x();
        para_Ex_Pose[i][4] = q.y();
        para_Ex_Pose[i][5] = q.z();
        para_Ex_Pose[i][6] = q.w();
    }

    VectorXd dep = f_manager.getDepthVector();
    for (int i = 0; i < f_manager.getFeatureCount(); i++)
        para_Feature[i][0] = dep(i);
    if (ESTIMATE_TD)
        para_Td[0][0] = td;
}

可以看出来，这里面生成的优化变量由：
para_Pose（6维，相机位姿）、
para_SpeedBias（9维，相机速度、加速度偏置、角速度偏置）、
para_Ex_Pose（6维、相机IMU外参）、
para_Feature（1维，特征点深度）、
para_Td（1维，标定同步时间）
五部分组成，在后面进行边缘化操作时这些优化变量都是当做整体看待。

2.1 MarginalizationInfo类分析

然后，我们先看下和边缘化类MarginalizationInfo

class MarginalizationInfo
{
  public:
    ~MarginalizationInfo();
    int localSize(int size) const;
    int globalSize(int size) const;
    //添加参差块相关信息（优化变量，待marg的变量）
    void addResidualBlockInfo(ResidualBlockInfo *residual_block_info);
    //计算每个残差对应的雅克比，并更新parameter_block_data
    void preMarginalize();
    //pos为所有变量维度，ｍ为需要marg掉的变量，ｎ为需要保留的变量
    void marginalize();
    std::vector getParameterBlocks(std::unordered_map &addr_shift);

    std::vector factors;//所有观测项
    int m, n;//m为要边缘化的变量个数，n为要保留下来的变量个数
    std::unordered_map parameter_block_size; //<优化变量内存地址,localSize>
    int sum_block_size;
    std::unordered_map parameter_block_idx; //<优化变量内存地址,在矩阵中的id>
    std::unordered_map parameter_block_data;//<优化变量内存地址,数据>

    std::vector keep_block_size; //global size
    std::vector keep_block_idx;  //local size
    std::vector keep_block_data;

    Eigen::MatrixXd linearized_jacobians;
    Eigen::VectorXd linearized_residuals;
    const double eps = 1e-8;
};

先说变量，这里有三个unordered_map相关的变量分别是：
parameter_block_size、
parameter_block_idx、
parameter_block_data，
他们的key都同一是long类型的内存地址，而value分别是，各个优化变量的长度，各个优化变量在id以各个优化变量对应的double指针类型的数据。
对应的有三个vector相关的变量分别是：
keep_block_size、
keep_block_idx、
keep_block_data，
他们是进行边缘化之后保留下来的各个优化变量的长度，各个优化变量在id以各个优化变量对应的double指针类型的数据
还有
linearized_jacobians、
linearized_residuals，
分别指的是边缘化之后从信息矩阵恢复出来雅克比矩阵和残差向量

2.3 第一步：调用addResidualBlockInfo()

对于函数我们直接看optimization中的调用会更直观，首先会调用addResidualBlockInfo()函数将各个残差以及残差涉及的优化变量添加入上面所述的优化变量中：
首先添加上一次先验残差项：

if (last_marginalization_info)
{
	vector drop_set;
	for (int i = 0; i < static_cast(last_marginalization_parameter_blocks.size()); i++)//last_marginalization_parameter_blocks是上一轮留下来的残差块
	{
	    if (last_marginalization_parameter_blocks[i] == para_Pose[0] ||
	        last_marginalization_parameter_blocks[i] == para_SpeedBias[0])//需要marg掉的优化变量，也就是滑窗内第一个变量
	        drop_set.push_back(i);
	}
	// construct new marginlization_factor
	MarginalizationFactor *marginalization_factor = new MarginalizationFactor(last_marginalization_info);
	ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(marginalization_factor, NULL,
	                                                               last_marginalization_parameter_blocks,
	                                                               drop_set);
	marginalization_info->addResidualBlockInfo(residual_block_info);
}

然后添加第0帧和第1帧之间的IMU预积分值以及第0帧和第1帧相关优化变量

{
    if (pre_integrations[1]->sum_dt < 10.0)
    {
        IMUFactor* imu_factor = new IMUFactor(pre_integrations[1]);
        ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(imu_factor, NULL,
                                                                   vector{para_Pose[0], para_SpeedBias[0], para_Pose[1], para_SpeedBias[1]},//优化变量
                                                                   vector{0, 1});//这里是0,1的原因是0和1是para_Pose[0], para_SpeedBias[0]是需要marg的变量
        marginalization_info->addResidualBlockInfo(residual_block_info);
    }
}

最后添加第一次观测滑窗中第0帧的路标点以及其他相关的滑窗中的帧的相关的优化变量

{
    int feature_index = -1;
    for (auto &it_per_id : f_manager.feature)
    {
        it_per_id.used_num = it_per_id.feature_per_frame.size();//这里是遍历滑窗所有的特征点
        if (!(it_per_id.used_num >= 2 && it_per_id.start_frame < WINDOW_SIZE - 2))
            continue;

        ++feature_index;

        int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;//这里是从特征点的第一个观察帧开始
        if (imu_i != 0)//如果第一个观察帧不是第一帧就不进行考虑，因此后面用来构建marg矩阵的都是和第一帧有共视关系的滑窗帧
            continue;

        Vector3d pts_i = it_per_id.feature_per_frame[0].point;

        for (auto &it_per_frame : it_per_id.feature_per_frame)
        {
            imu_j++;
            if (imu_i == imu_j)
                continue;

            Vector3d pts_j = it_per_frame.point;
            if (ESTIMATE_TD)
            {
                ProjectionTdFactor *f_td = new ProjectionTdFactor(pts_i, pts_j, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocity,
                                                                  it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td,
                                                                  it_per_id.feature_per_frame[0].uv.y(), it_per_frame.uv.y());
                ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(f_td, loss_function,
                                                                                vector{para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index], para_Td[0]},//优化变量
                                                                                vector{0, 3});
                marginalization_info->addResidualBlockInfo(residual_block_info);
            }
            else
            {
                ProjectionFactor *f = new ProjectionFactor(pts_i, pts_j);
                ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(f, loss_function,
                                                                               vector{para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index]},//优化变量
                                                                               vector{0, 3});//为0和3的原因是，para_Pose[imu_i]是第一帧的位姿，需要marg掉，而3是para_Feature[feature_index]是和第一帧相关的特征点，需要marg掉
                marginalization_info->addResidualBlockInfo(residual_block_info);
            }
        }
    }
}

上面添加残差以及优化变量的方式和后端线性优化中添加的方式相似，因为边缘化类应该就是仿照ceres写的，我们可以简单剖析下上面的操作，
第一步定义损失函数，对于先验残差就是MarginalizationFactor，对于IMU就是IMUFactor，对于视觉就是ProjectionTdFactor，这三个损失函数的类都是继承自ceres的损失函数类ceres::CostFunction，里面都重载了函数

virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const;

这个函数通过传入的优化变量值parameters，以及先验值（对于先验残差就是上一时刻的先验残差last_marginalization_info，对于IMU就是预计分值pre_integrations[1]，对于视觉就是空间的的像素坐标pts_i, pts_j）可以计算出各项残差值residuals，以及残差对应个优化变量的雅克比矩阵jacobians。

第二步定义ResidualBlockInfo，其构造函数如下

ResidualBlockInfo(ceres::CostFunction *_cost_function, ceres::LossFunction *_loss_function, std::vector _parameter_blocks, std::vector _drop_set)

这一步是为了将不同的损失函数_cost_function以及优化变量_parameter_blocks统一起来再一起添加到marginalization_info中。变量_loss_function是核函数，在VINS-mono的边缘化中仅仅视觉残差有用到couchy核函数，另外会设置需要被边缘话的优化变量的位置_drop_set，这里对于不同损失函数又会有不同：
对于先验损失，其待边缘化优化变量是根据是否等于para_Pose[0]或者para_SpeedBias[0]，也就是说和第一帧相关的优化变量都作为边缘化的对象。
对于IMU，其输入的_drop_set是vector{0, 1}，也就是说其待边缘化变量是para_Pose[0], para_SpeedBias[0]，也是第一政相关的变量都作为边缘化的对象，这里值得注意的是和后端优化不同，这里只添加了第一帧和第二帧的相关变量作为优化变量，因此边缘化构造的信息矩阵会比后端优化构造的信息矩阵要小
对于视觉，其输入的_drop_set是vector{0, 3}，也就是说其待边缘化变量是para_Pose[imu_i]和para_Feature[feature_index]，从这里可以看出来在VINS-mono的边缘化操作中会不仅仅会边缘化第一帧相关的优化变量，还会边缘化掉以第一帧为起始观察帧的路标点。

第三步是将定义的residual_block_info添加到marginalization_info中，通过下面这一句

marginalization_info->addResidualBlockInfo(residual_block_info);

然后可以看下addResidualBlockInfo()这个函数的实现如下：

void MarginalizationInfo::addResidualBlockInfo(ResidualBlockInfo *residual_block_info)
{
    factors.emplace_back(residual_block_info);

    std::vector ¶meter_blocks = residual_block_info->parameter_blocks;//parameter_blocks里面放的是marg相关的变量
    std::vector parameter_block_sizes = residual_block_info->cost_function->parameter_block_sizes();

    for (int i = 0; i < static_cast(residual_block_info->parameter_blocks.size()); i++)//这里应该是优化的变量
    {
        double *addr = parameter_blocks[i];//指向数据的指针
        int size = parameter_block_sizes[i];//因为仅仅有地址不行，还需要有地址指向的这个数据的长度
        parameter_block_size[reinterpret_cast(addr)] = size;//将指针强转为数据的地址
    }

    for (int i = 0; i < static_cast(residual_block_info->drop_set.size()); i++)//这里应该是待边缘化的变量
    {
        double *addr = parameter_blocks[residual_block_info->drop_set[i]];//这个是待边缘化的变量的id
        parameter_block_idx[reinterpret_cast(addr)] = 0;//将需要marg的变量的id存入parameter_block_idx
    }
}

这里其实就是分别将不同损失函数对应的优化变量、边缘化位置存入到parameter_block_sizes和parameter_block_idx中，这里注意的是执行到这一步，parameter_block_idx中仅仅有待边缘化的优化变量的内存地址的key，而且其对应value全部为0

2.4 第二步：调用preMarginalize()

上面通过调用addResidualBlockInfo()已经确定优化变量的数量、存储位置、长度以及待优化变量的数量以及存储位置，下面就需要调用preMarginalize()进行预处理，preMarginalize()实现如下：

void MarginalizationInfo::preMarginalize()
{
    for (auto it : factors)//在前面的addResidualBlockInfo中会将不同的残差块加入到factor中
    {
        it->Evaluate();//利用多态性分别计算所有状态变量构成的残差和雅克比矩阵

        std::vector block_sizes = it->cost_function->parameter_block_sizes();
        for (int i = 0; i < static_cast(block_sizes.size()); i++)
        {
            long addr = reinterpret_cast(it->parameter_blocks[i]);//优化变量的地址
            int size = block_sizes[i];
            if (parameter_block_data.find(addr) == parameter_block_data.end())//parameter_block_data是整个优化变量的数据
            {
                double *data = new double[size];
                memcpy(data, it->parameter_blocks[i], sizeof(double) * size);//重新开辟一块内存
                parameter_block_data[addr] = data;//通过之前的优化变量的数据的地址和新开辟的内存数据进行关联
            }
        }
    }
}

其中 it->Evaluate()这一句里面其实就是调用各个损失函数中的重载函数Evaluate()，这个函数前面有提到过，就是

virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const;

这个函数通过传入的优化变量值parameters，以及先验值（对于先验残差就是上一时刻的先验残差last_marginalization_info，对于IMU就是预计分值pre_integrations[1]，对于视觉就是空间的的像素坐标pts_i, pts_j）可以计算出各项残差值residuals，以及残差对应个优化变量的雅克比矩阵jacobians。此外这里会给parameter_block_data赋值，这里引用崔华坤老师写的《VINS 论文推导及代码解析》中的例子

parameter_block_sizes中的key值就是上表中的左边第一列，value值就是上表中的中间一列（localSize）
parameter_block_data中的key值就是上表中的左边第一列，value值就是上表中的右边第一列（double*的数据）

2.5 第三步：调用marginalize()

前面两步已经将数据都准备好了，下面通过调用marginalize()函数就要正式开始进行边缘化操作了，实现如下：

void MarginalizationInfo::marginalize()
{
    int pos = 0;
    for (auto &it : parameter_block_idx)//遍历待marg的优化变量的内存地址
    {
        it.second = pos;
        pos += localSize(parameter_block_size[it.first]);
    }

    m = pos;//需要marg掉的变量个数

    for (const auto &it : parameter_block_size)
    {
        if (parameter_block_idx.find(it.first) == parameter_block_idx.end())//如果这个变量不是是待marg的优化变量
        {
            parameter_block_idx[it.first] = pos;//就将这个待marg的变量id设为pos
            pos += localSize(it.second);//pos加上这个变量的长度
        }
    }

    n = pos - m;//要保留下来的变量个数

    //通过上面的操作就会将所有的优化变量进行一个伪排序，待marg的优化变量的idx为0，其他的和起所在的位置相关

    TicToc t_summing;
    Eigen::MatrixXd A(pos, pos);//整个矩阵A的大小
    Eigen::VectorXd b(pos);
    A.setZero();
    b.setZero();
   
    TicToc t_thread_summing;
    pthread_t tids[NUM_THREADS];
    ThreadsStruct threadsstruct[NUM_THREADS];
    int i = 0;
    for (auto it : factors)//将各个残差块的雅克比矩阵分配到各个线程中去
    {
        threadsstruct[i].sub_factors.push_back(it);
        i++;
        i = i % NUM_THREADS;
    }
    for (int i = 0; i < NUM_THREADS; i++)
    {
        TicToc zero_matrix;
        threadsstruct[i].A = Eigen::MatrixXd::Zero(pos,pos);
        threadsstruct[i].b = Eigen::VectorXd::Zero(pos);
        threadsstruct[i].parameter_block_size = parameter_block_size;
        threadsstruct[i].parameter_block_idx = parameter_block_idx;
        int ret = pthread_create( &tids[i], NULL, ThreadsConstructA ,(void*)&(threadsstruct[i]));//分别构造矩阵
        if (ret != 0)
        {
            ROS_WARN("pthread_create error");
            ROS_BREAK();
        }
    }
    for( int i = NUM_THREADS - 1; i >= 0; i--)  
    {
        pthread_join( tids[i], NULL ); 
        A += threadsstruct[i].A;
        b += threadsstruct[i].b;
    }

    //TODO
    Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());
    Eigen::SelfAdjointEigenSolver saes(Amm);
    Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() * saes.eigenvectors().transpose();

    //舒尔补
    Eigen::VectorXd bmm = b.segment(0, m);
    Eigen::MatrixXd Amr = A.block(0, m, m, n);
    Eigen::MatrixXd Arm = A.block(m, 0, n, m);
    Eigen::MatrixXd Arr = A.block(m, m, n, n);
    Eigen::VectorXd brr = b.segment(m, n);
    A = Arr - Arm * Amm_inv * Amr;
    b = brr - Arm * Amm_inv * bmm;//这里的A和b应该都是marg过的A和b,大小是发生了变化的

    //下面就是更新先验残差项
    Eigen::SelfAdjointEigenSolver saes2(A);//求特征值
    Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
    Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));

    Eigen::VectorXd S_sqrt = S.cwiseSqrt();
    Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
}

第一步，秉承这map数据结构没有即添加，存在即赋值的语法，上面的代码会先补充parameter_block_idx，前面提到经过addResidualBlockInfo()函数仅仅带边缘化的优化变量在parameter_block_idx有key值，这里会将保留的优化变量的内存地址作为key值补充进去，并统一他们的value值是其前面已经放入parameter_block_idx的优化变量的维度之和，同时这里会计算出两个变量m和n，他们分别是待边缘化的优化变量的维度和以及保留的优化变量的维度和。

第二步，函数会通过多线程快速构造各个残差对应的各个优化变量的信息矩阵（雅克比和残差前面都已经求出来了），然后在加起来，如下图所示：

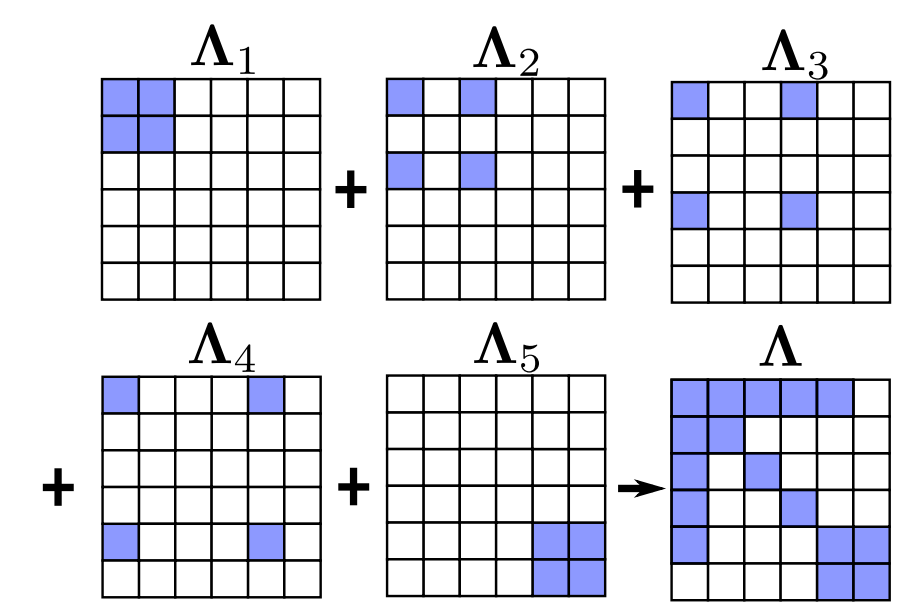
因为这里构造信息矩阵时采用的正是parameter_block_idx作为构造顺序，因此，就会自然而然地将待边缘化的变量构造在矩阵的左上方。

第三步，函数会通过shur补操作进行边缘化，然后再从边缘化后的信息矩阵中恢复出来雅克比矩阵linearized_jacobians和残差linearized_residuals，这两者会作为先验残差带入到下一轮的先验残差的雅克比和残差的计算当中去。

2.6 第四步：滑窗预移动

在optimization的最后会有一部滑窗预移动的操作，就是下面这一段代码

std::unordered_map addr_shift;
for (int i = 1; i <= WINDOW_SIZE; i++)//从1开始，因为第一帧的状态不要了
{
    //这一步的操作指的是第i的位置存放的的是i-1的内容，这就意味着窗口向前移动了一格
    addr_shift[reinterpret_cast(para_Pose[i])] = para_Pose[i - 1];//因此para_Pose这些变量都是双指针变量，因此这一步是指针操作
    addr_shift[reinterpret_cast(para_SpeedBias[i])] = para_SpeedBias[i - 1];
}
for (int i = 0; i < NUM_OF_CAM; i++)
    addr_shift[reinterpret_cast(para_Ex_Pose[i])] = para_Ex_Pose[i];
if (ESTIMATE_TD)
{
    addr_shift[reinterpret_cast(para_Td[0])] = para_Td[0];
}
vector parameter_blocks = marginalization_info->getParameterBlocks(addr_shift);

if (last_marginalization_info)
    delete last_marginalization_info;//删除掉上一次的marg相关的内容
last_marginalization_info = marginalization_info;//marg相关内容的递归
last_marginalization_parameter_blocks = parameter_blocks;//优化变量的递归，这里面仅仅是指针

值得注意的是，这里仅仅是相当于将指针进行了一次移动，指针对应的数据还是旧数据，因此需要结合后面调用的slideWindow()函数才能实现真正的滑窗移动，此外
last_marginalization_info就是保留下来的先验残差信息，包括保留下来的雅克比linearized_jacobians、残差linearized_residuals、保留下来的和边缘化有关的数据长度keep_block_size、顺序keep_block_idx以及数据keep_block_data。
last_marginalization_info就是保留下来的滑窗内的所有的优化变量

这里需要明确一个概念就是，边缘化操作并不会改变优化变量的值，而仅仅是改变了优化变量之间的关系，而这个关系就是通过信息矩阵体现的。

到此边缘化操作的流程就介绍完了，上面介绍的边缘化最老帧的情况，边缘化次新帧的方式类似，在此就不再赘述，如果有什么问题欢迎交流～