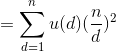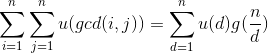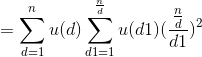【CCPC-Wannafly Winter Camp Day3 Div2 F 小清新数论】(莫比乌斯反演)
因为是第一次做出这种题,所以写个题解纪念一下。
题目描述
这是一道比较基础的数论题。
其中 gcd(i,j) 表示 i,j 的最大公约数,
表示莫比乌斯函数,它的一个等价定义是
,
当
时。
输入描述
输入一行包含一个整数 n(1≤n≤107)。
输出描述
输出一行一个整数,表示答案。答案可能很大,请对 998244353 取模后输出。
样例输入 1
5样例输出 1
14样例输入 2
100样例输出 2
3631
题意:
思路:
因为
所以
所以
如果直接暴力的话,时间复杂度是O(n^2),所以我们还需分块处理。
我们让d从1增到![]() ,再让
,再让![]() 从
从![]() 减到1,所以一次分块可以降O(
减到1,所以一次分块可以降O(![]() )的复杂度。
)的复杂度。
在求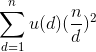 和
和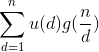 时,都可进行分块,每次分块可以降O(
时,都可进行分块,每次分块可以降O(![]() )的复杂度,两次可降O(n),所以最终时间复杂度为O(n)。
)的复杂度,两次可降O(n),所以最终时间复杂度为O(n)。
代码:
#include
using namespace std;
const int N=1e7+10;
const long long mo=998244353;
int u[N],sum[N];
long long pri[N>>1],now;
bool vis[N];
int n;
void init()
{
vis[1]=1;u[1]=1;
for(int i=2;i<=n;++i)
{
if(!vis[i])pri[++now]=i,u[i]=-1;
for(int j=1;j<=now&&(long long)pri[j]*i<=n;++j)
{
vis[pri[j]*i]=1;
u[pri[j]*i]=-u[i];
if(i%pri[j]==0){u[pri[j]*i]=0;break;}
}
}
for(int i=1;i<=n;i++)sum[i]=u[i]+sum[i-1];
}
long long g(int n)
{
long long ret = 0;
int x=(int)sqrt(double(n)),tx;
for(int i=1; i<=x; ++i)
{
ret+=(long long)u[i]*(n/i)%mo*(n/i)%mo;
ret%=mo;
}
for(int i=n/x;i>=1;--i)
{
tx=n/i;
ret+=(long long)(sum[tx]-sum[x])*i%mo*i%mo;
ret%=mo;
x=tx;
}
return ret;
}
int main()
{
scanf("%d",&n);
init();
long long ans = 0;
u[1]=1;
int x=(int)sqrt(double(n)),tx;
for(int i=1; i<=x; ++i)
{
ans+=(long long)u[i]*g(n/i)%mo;
ans%=mo;
}
for(int i=n/x;i>=1;--i)
{
tx=n/i;
ans+=(long long)(sum[tx]-sum[x])*g(i)%mo;
ans%=mo;
x=tx;
}
printf("%lld\n",(ans+mo)%mo);
return 0;
}
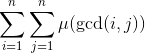
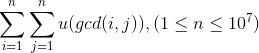
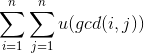
![=\sum_{d=1}^{n}\sum_{i=1}^{n}\sum_{j=1}^{n}u(d)[gcd(i,j)==d]](http://img.e-com-net.com/image/info8/f1b1b961fba44ca18295c3c53c1f534d.gif)
![=\sum_{d=1}^{n}u(d)\sum_{i=1}^{n}\sum_{j=1}^{n}[gcd(i,j)==d]](http://img.e-com-net.com/image/info8/155a2921ff364f84a7e8ce427ace9a14.gif)
![=\sum_{d=1}^{n}u(d)\sum_{i=1}^{\frac{n}{d}}\sum_{j=1}^{\frac{n}{d}}[gcd(i,j)==1]](http://img.e-com-net.com/image/info8/247ae04c795247aa982206cb3f22ba6e.gif)
![g(n)=\sum_{i=1}^{n}\sum_{j=1}^{n}[gcd(i,j)==1]](http://img.e-com-net.com/image/info8/ca7cebe798eb47d3a2eccb9119942aa3.gif)
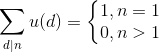
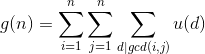
![=\sum_{d=1}^{n}u(d)\sum_{i=1}^{n}\sum_{j=1}^{n}[d|gcd(i,j)]](http://img.e-com-net.com/image/info8/39c21e4a043640debaf7b2c1f9a4ad25.gif)