2020牛客暑期多校训练营(第二场)(BCDF题解)
题目大意:
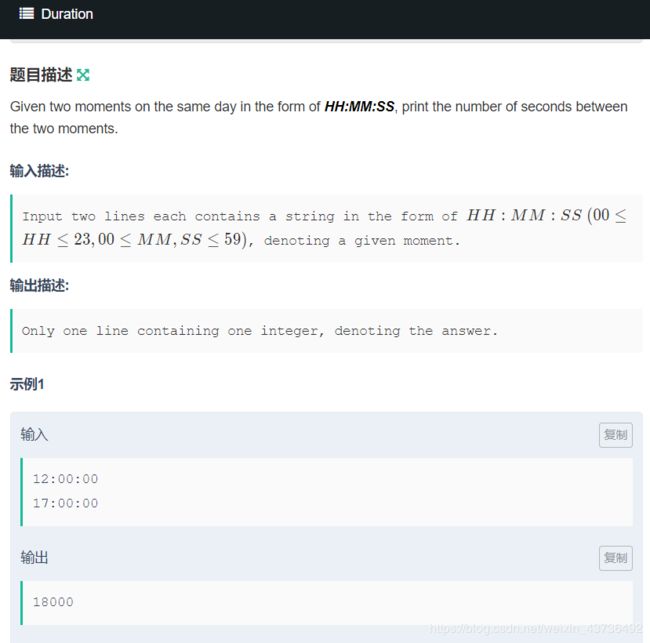
给你两个时间,要你求他们差了多少秒。
思路:
python的datetime搞搞就好了。
代码:
import datetime
if __name__ == "__main__":
d1 = input()
d2 = input()
d1 = datetime.datetime.strptime(d1, "%H:%M:%S")
d2 = datetime.datetime.strptime(d2, "%H:%M:%S")
if(d1 > d2):
seconds = (d1 - d2).seconds
else :
seconds = (d2 - d1).seconds
print(seconds)
题目大意:
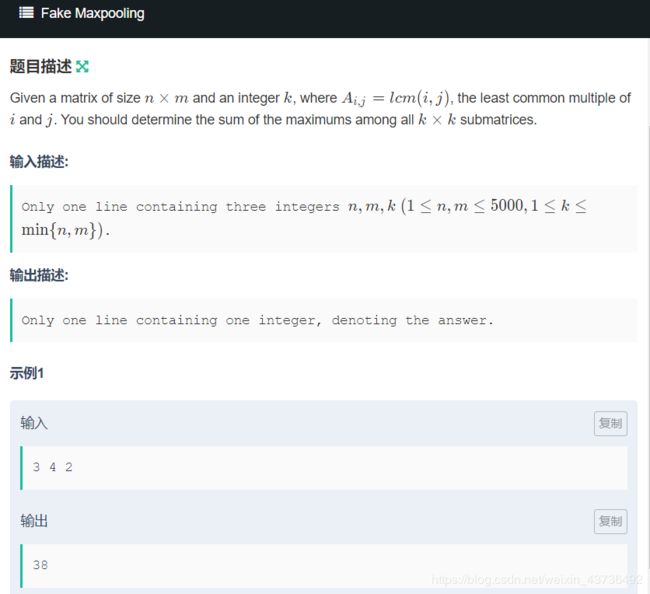
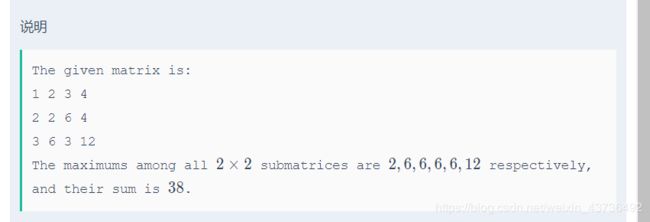
给你一个 n ∗ m n*m n∗m的矩阵,其中 a i j = l c m ( i , j ) aij=lcm(i,j) aij=lcm(i,j),现在给你一个 k k k要你求所有 k ∗ k k*k k∗k子矩阵的最大值之和。
思路:
这题对时间和空间卡得非常紧,构造矩阵的时候因为是对称矩阵只要求一半就行了,如果全部求出来就会超时,矩阵的类型开 i n t int int,不然超空间。
然后这题就是一个二维平面区间最大值问题了,可以用二维线段树,但是会超空间,所以这里我用的是单调队列维护二维平面最大值,最后求一下和就好了。
代码:
#include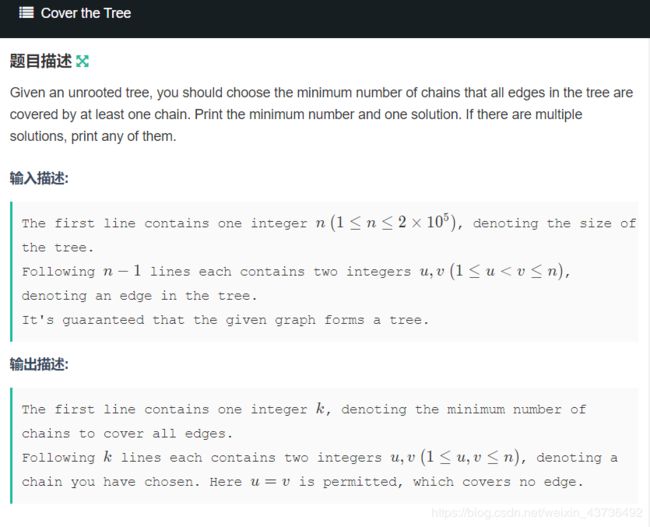
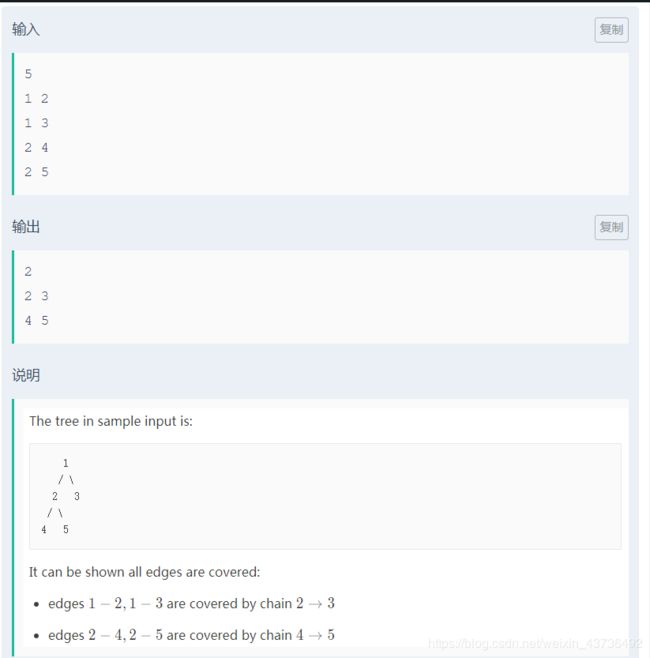
题目大意:给你一颗无根树,要你找最少的链使得每条边至少被走过一次。
思路:
这题场上没写出来真是智商欠费了,这充其量是一道思维题,我们可以从一个叶子节点出发,当我们不到另外一个叶子节点停下来的时候,我们基本可以走完所有边(除了其他叶子节点的边),所以最少数量不会超过 n / 2 n/2 n/2向上取整,其中 n n n是叶子节点个数。然后我们再构造一种走法使得所有的叶子节点至少被走过一次就行了,这里采用标程的方法 l ( 1 ) − > l ( n / 2 + 1 ) , l ( 2 ) − > l ( n / 2 + 2 ) . . . . . l(1)->l(n/2+1),l(2)->l(n/2+2)..... l(1)−>l(n/2+1),l(2)−>l(n/2+2).....。
求叶子节点顺序是用的 d f s dfs dfs序。
代码:
#include
for(int i = 0; i < ans; i++){
cout<<dfn[i] + 1<<" "<<dfn[(cnt/2+i)%cnt] + 1<<endl;
}
return 0;
}
题目大意:
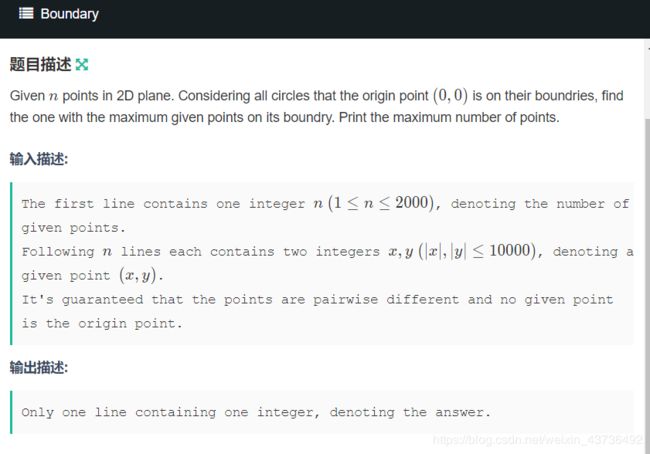
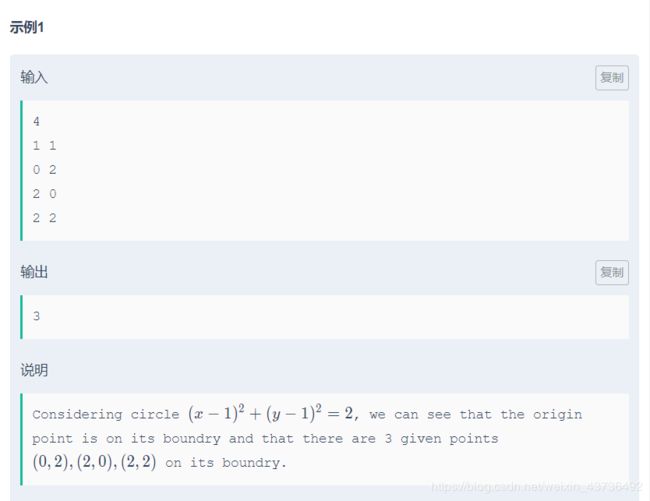
在二维平面上给你 n n n个坐标,要你确定一个圆,使得这些点经过这个圆尽可能多。
思路:
三点确定一个圆,枚举两个点与圆点 ( 0 , 0 ) (0,0) (0,0)确定一个圆,求出圆心的坐标并且保存起来,然后统计圆心出现的次数,次数最多的是答案 a n s ans ans,不过还要求一下组合数,我们设答案为 x x x,因为我们从 x x x点取两个求的圆心,所以是 C ( x , 2 ) = x ∗ ( x − 1 ) = a n s ∗ 2 C(x,2)=x*(x-1)=ans*2 C(x,2)=x∗(x−1)=ans∗2。最后枚举一下答案就行了,找到满足这个条件的。
这题会卡 m a p map map,只能自己排序然后统计个数。
代码:
#include