2020暑假牛客多校第二场 I - Interval

没啥好说的，我又躺了一场
比赛地址

I–Interval

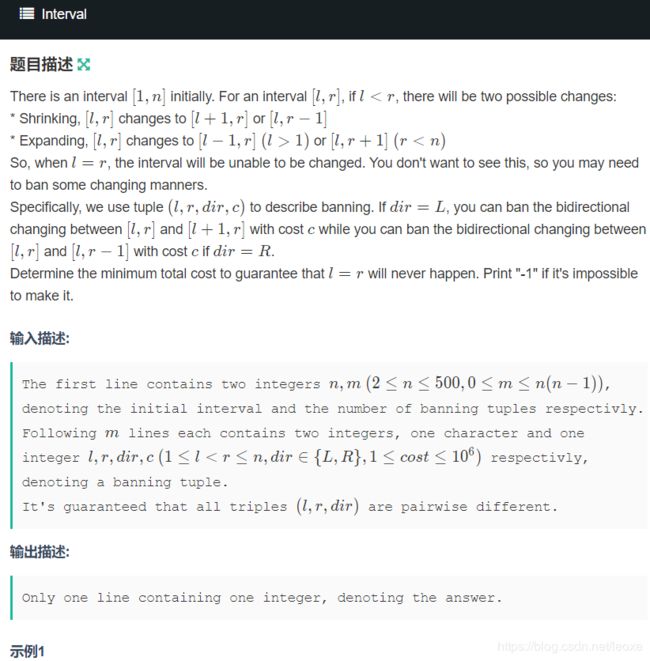
嗷，大意就是初始为$(1...n)$，然后你需要阻止它的左边界等于右边界，也就是$L==R$的情况不能出现 ，你可以阻挡若干条变化，每个阻挡都有自己的花费，求问最少花费为多少，或者说根本不可以阻挡
阻断格式为$u,v,ch,w$
$ch==L$
$(u,v)--(u+1,v)$被阻断
$ch==R$
$(u,v)--(u,v-1)$被阻断
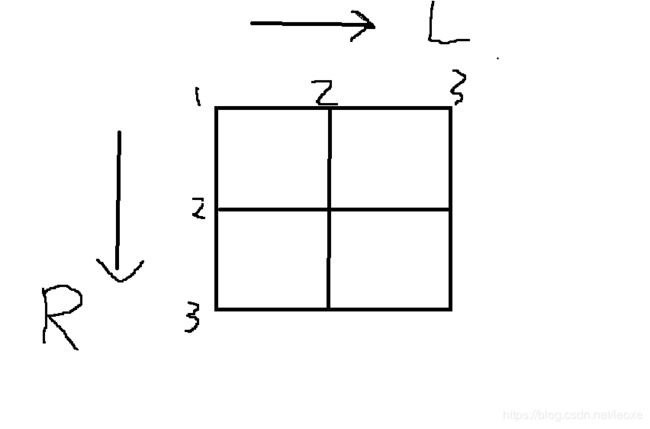
也就是如下图
方便起见，下边图都是L与R交换了方向的， 注意坐标，
以样例来画图

3 4
1 3 L 10
1 3 R 3
1 2 L 1
1 2 R 1

那么原图是

阻断的边是
$(1,3)-(2,3)-10$
$(1,3)-(1,2)-3$
$(1,2)-(2,2)-1$
$(1,2)-(1,1)-1$
所以图变成了，
（没涉及的边属于不可隔绝，流量设为inf，之后求最小割，如果最小割大于inf则说明不可切断，反之则可以切断完）

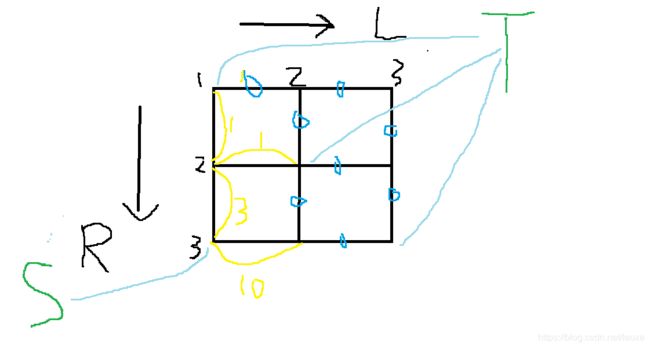
绿色为起始点与终点，黄边为可以切断的，蓝边为不可切断的
把起始点$(1,n)$与源点连边，把可以切断的边赋值，不能切断的都设置为$inf$,之后把所有$(x,y),x==y$的点都与虚拟汇点相连，这个时候求最小割求出来的就是需要花费的，如果最小割大于inf则代表无法阻断
但是这题由于是网格图，且$n$的数据范围到达了$5e2$，$m$复杂度到达了$2e5$，而$dinic$算法复杂度为$n^{2}m$，这直接超时到自闭…
所以这时候需要引入一个技巧，
平面图求最小割转换为对偶图求最短路
不明白定义的可以去百度，也有个例题是$BZOJ$的狼抓兔子那题
大致思路是把每一个小的平面图转换为一个点，然后点与点之间的权值就是这中间的横跨那条边的权值…然后跑出来的最短路就是最小割…
先放出建立出来的对偶图

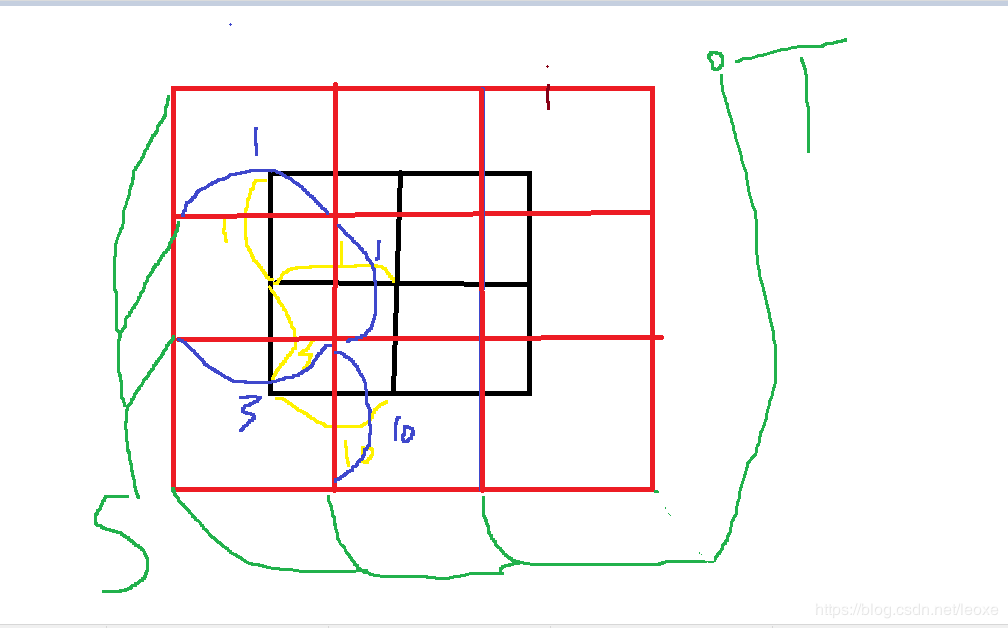
绿边建立为0，蓝边为原始的，然后直接跑最短路，跑出来是多少答案就是多少，如果不可到达，那就是无法阻断
喜闻乐见的$code$环节

#include 
using namespace std;
typedef long long  LL;
const int maxn = 6e2 + 7;
const LL inf = 2e18 + 7;
struct qnode {
    LL u, w;
    qnode(LL _u = 0, LL _w = 0)
        : u(_u), w(_w) {}
    bool operator < (const qnode& b) const {
        return w > b.w;
    }
};
struct Edge {
    LL v, w;
    Edge(LL _v, LL _w) 
        : v(_v), w(_w) {}
};
priority_queue<qnode> Q;
vector<Edge> G[maxn * maxn];
void add_edge(LL u, LL v, LL w) {
    G[u].push_back(Edge(v, w));
    G[v].push_back(Edge(u, w));
}
LL dis[maxn * maxn];
bool used[maxn * maxn];
LL n, m;
inline LL id(LL x, LL y) {
    return x * (n + 1) + y;
}
void Dijstra(int st) {
    for(int i = 0; i <= n + 1; ++ i) {
        for(int j = 0; j <= n + 1; ++ j) {
            dis[id(i,j)] = inf;
            used[id(i,j)] = false;
        }
    }
    dis[st] = 0;
    Q.push(qnode(st, dis[st]));
    while(!Q.empty()) {
        LL u = Q.top().u;
        Q.pop();
        if(used[u]) {
            continue;
        }
        used[u] = true;
        for(int i = 0; i < G[u].size(); ++ i) {
            int v = G[u][i].v;
            if(dis[v] > dis[u] + G[u][i].w) {
                dis[v] = dis[u] + G[u][i].w;
                Q.push(qnode(v, dis[v]));
            }
        }
    }
    if(dis[id(n + 1, n + 1)] == inf) {
        cout << -1 << endl;
    } else {
        cout << dis[id(n + 1, n + 1)] << endl;
    }
}
int main () {
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    
    cin >> n >> m;
    LL u, v, w;
    char ch;
    while(m --) {
        cin >> u >> v >> ch >> w;
        if(ch == 'L') {
            add_edge(id(v, u + 1), id(v + 1, u + 1), w);
        } else {
            add_edge(id(v, u), id(v, u + 1), w);
        }
    }
    for(int i = 1; i <= n; ++ i) {
        add_edge(id(0, 0), id(i, 1), 0);
        add_edge(id(n + 1,i), id(n + 1, n + 1), 0);
    }
    Dijstra(0);
    #ifdef _LOCALE_PAUSE_
        system("pause");
    #endif
    return 0;
}

完结撒花啦