HDU 6814 Tetrahedron 2020杭电多校第五场 (数学推导)
原题题面
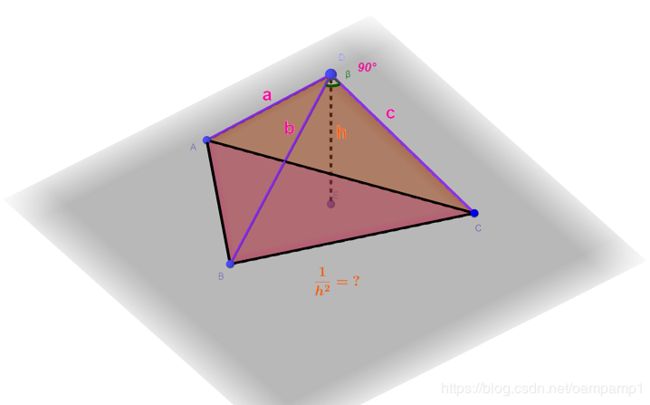
Generate three integers a, b, and c in [ 1 , n ] [1,n] [1,n] with equal probability independently, and use them as the three right-angle side length of a right-angled tetrahedron. Find the expectation of the reciprocal square of the distance from the right-angle apex to the slope (Euclidean distance).
For each test case, output a line containing the answer mod 998244353.
输入格式
In the first line, you should read an integer T denoting the number of test cases.
In every test case, the only line will include an integer n.
It is guaranteed that T is no larger than 2 × 1 0 6 2×10^6 2×106 and n is no larger than 6 × 1 0 6 6×10^6 6×106.
输出格式
For each test case, output the only line containing just one integer denoting the answer mod 998244353.
输入样例
3
1
2
3
输出样例
3
124780546
194103070
题面分析
给定n,在[1,n]中等概率随机选出3个数 a , b , c a,b,c a,b,c(可以重复),做直角四面体(a,b,c三遍两两垂直),记顶点到底面的距离为 h h h求,期望 E ( 1 h 2 ) E(\frac{1}{h^2}) E(h21)。
直接考虑 n ≥ 3 n\geq3 n≥3的情况。
首先要做的自然就是求出 h h h。
把 a , b , c a,b,c a,b,c看作三个坐标轴,顶点看作原点后即可建系。
设平面为 x + A y + B z = C x+Ay+Bz=C x+Ay+Bz=C,代入 ( a , 0 , 0 ) , ( 0 , b , 0 ) , ( 0 , 0 , c ) (a,0,0),(0,b,0),(0,0,c) (a,0,0),(0,b,0),(0,0,c)后得到平面为 x + a b y + a c z = a x+\frac{a}{b}y+\frac{a}{c}z=a x+bay+caz=a
那 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)到该平面距离为
h = ∣ a ∣ 1 2 + ( a b ) 2 + ( a c ) 2 h=\frac{|a|}{\sqrt{1^2+(\frac{a}{b})^2+(\frac{a}{c})^2}} h=12+(ba)2+(ca)2∣a∣
= 1 1 a 2 + 1 b 2 + 1 c 2 =\sqrt{\frac{1}{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}} =a21+b21+c211
那么 1 h 2 = 1 a 2 + 1 b 2 + 1 c 2 \frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2} h21=a21+b21+c21
然后我们可以计算发现,对于在 [ 1 , n ] [1,n] [1,n]等概率选取的 a , b , c a,b,c a,b,c的所有方案中。
n n n个数字出现的次数是相等的,都是 n 2 n^{2} n2( a a a确定后, b , c b,c b,c各有 n n n种选法)。
所以最后的答案 E ( 1 h 2 ) = 3 n 2 ∑ i = 1 n 1 i 2 n 3 = 3 ∑ i = 1 n 1 i 2 n E(\frac{1}{h^2})=\frac{3n^{2}\sum_{i=1}^{n}\frac{1}{i^2}}{n^3}=\frac{3\sum_{i=1}^{n}\frac{1}{i^2}}{n} E(h21)=n33n2∑i=1ni21=n3∑i=1ni21
AC代码(1968ms)
#include 后记
可以叉积,可以海伦公式,能搞的方法很多,只要老老实实算就能出答案。
DrGilbert 2020.8.4