专题·约瑟夫问题集锦【including 约瑟夫问题，约瑟夫环，反约瑟夫问题，好人坏人……
初见安~这里是约瑟夫专题 & 数论专题（5）~【详见数论专栏
不要小瞧约瑟夫哦~【预防针
//题目来自于某入门OJ
一、出队顺序
Description
有M个人，其编号分别为1－M。这M个人按顺序排成一个圈。现在给定一个数N，从第一个人开始依次报数，数到N的人出列，然后又从下一个人开始又从1开始依次报数，数到N的人又出列．．．如此循环，直到最后一个人出列为止。
Input
输入只有一行，包括2个整数M（8 <= M <= 15 )，N( 5 <= N <= 32767 )。之间用一个空格分开。
Output
输出M行，每行一个整数。
Sample Input
8 5Sample Output
5
2
8
7
1
4
6
3Sol
看数据范围这么小，咱们直接爆搜是肯定没问题的。所以直接上代码了。
#include
using namespace std;
int n, m;
bool vis[200];
int main()
{
scanf("%d%d", &n, &m);
int t = 0, tot = n;
while(tot > 0)//人数
{
int cnt = 0;
while(1)
{
t++;
if(t > n) t %= n;
if(!vis[t]) cnt++;
if(cnt == m) break;//数到m
}
printf("%d\n", t);
vis[t] = 1;tot--;
}
return 0;
} 二、最后一人的位置
1.小范围
Description
Zerg包围了你的城市，并准备对在此举行祭旗仪式。仪式是这样举行的：n个祭品（就是人类）编号1...n，排成一
圈，从1号开始，每隔一个，便将一个祭品送进Spawning Pool（就是把人变成虫子的地方啦），直到最后剩下一个
人，Zerg会把他放掉。Zerg认为这样做会给他们的战争带来好运。现在，没有丝毫反抗能力的你为了活命，必须站
在那个最后被剩下的位置。幸好你手中有一台电脑，它可以帮你迅速决定站在哪里。
Input
第1行 一个正整数k(1<=k<=30000)，表示下面有k组测试数据。
以下k行 每行一个正整数n(1<=n<=30000)，表示n个人被抓来祭旗
注意： 有50%的数据k<=500。
Output
共k行 对于输入的每个n输出一个正整数，表示应该站在哪个位置能生还。
Sample Input
3
5
10
100Sample Output
3
5
73Sol
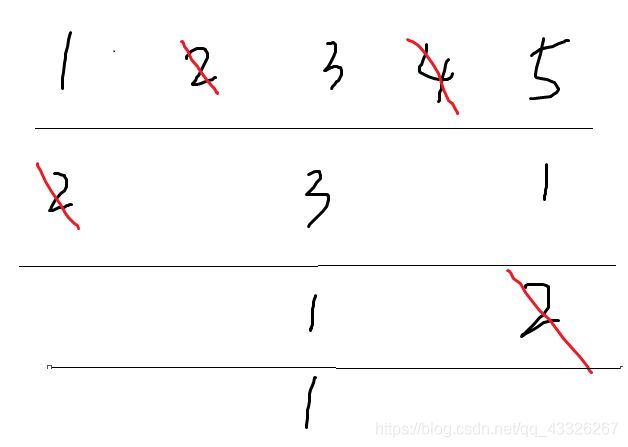
虽然我标的是小范围，但是如果我们暴力模拟是一定会超时的。所以我们就尝试一下能不能用数学方法简化一下过程——运用到重新标号的方法，每到一轮我们就给他们重新排个序，这样的话到了最后一个人他的序号就是1。这道题的话就相当于n个人，m = 2，求最后一个人的编号。我们可以举个例子：n = 5时，编号过程如下：
所以可以看出：最后活下来的人是3号，中途的序号为：3，3，1，1。那么我们可以开始思考：既然最后一个人的编号一定是1，怎么逆推回去呢？我们再仔细观察重新编号的这个过程，可以看出：1 = (1 + 2) % 2。所以可以得到这么一个式子：
，i为当前轮人数。那么问题就来了：再往上推，mod就会出现为0的情况了。所以我们需要mod的不是n，而是（ｎ-1）。这样看起来又会比较麻烦，我们倒也不如直接从0开始编号，编排为0 ~n -1，这样就可以直接用刚刚得出的递推公式了。一共进行n - 1轮，时间复杂度不过O（n），所以代码如下：
#include
using namespace std;
int n[30005], N = 0, t;
int ans[30005];
void init(int maxn)
{
for(int i = 2; i <= maxn; i++)
ans[i] = (ans[i - 1] + 2) % i;//要预处理，否则O（kn）还是会爆
}
int main()
{
scanf("%d", &t);
for(int i = 1; i <= t; i++)
{
scanf("%d", &n[i]);
N = max(N, n[i]);//为了省小范围数据的时间，取个上界
}
init(N);
for(int i = 1; i <= t; i++)
printf("%d\n", ans[n[i]] + 1);//下标从0开始， 最后要+1
return 0;
} 2.大范围
Description
一开始有n个人围成一个圈,从1开始顺时针报数,报出m的人被机关处决.然后下一个人再从1开始报数,直到只剩下一
个人
Input
第一行一个整数T,表示数据组数.
接下来T行,每行两个整数n,m.
1 ≤ T ≤ 20, 1 ≤ n ≤ 10^9, 1 ≤ m ≤ 10^5
Output
对于每组数据,输出一行一个整数,表示幸存者的编号.
Sample Input
5
4 6
2 8
2 9
8 8
7 9Sample Output
3
1
2
4
7Sol
在n的这种范围下，即使是O（n）也会爆炸了。怎么办呢？似乎这个递推公式已经是极简了。但是我们仍然可以发现一个问题——当i >>m和ans时，mod i已经没有任何作用了，相当于一个多余的操作。那么我们可以尝试着跳过这些多余的操作，一步登天【划掉】，也就是说当有ans + m < i时，就特殊处理一下，直接ans += m * step，并且让i += step。
当然，当i + step > n的时候，我们就只能让step = n - i +１了。
来看下代码和详解吧～
#include
using namespace std;
int n, m, t;
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%d%d", &n, &m);
int ans = 0, step = 0;
if(m == 1) ans = n - 1;//预处理
else if(n == 1) ans = 0;
else
{
for(int i = 2; i <= n; )
{
if(ans + m < i)//可以尝试跳过步骤
{
step = (i - 1 - ans) % (m - 1)?(i - 1 - ans) / (m - 1) : (i - 1 - ans) / (m - 1) - 1;//注意是从0开始编号的哦。
step = ceil((i - 1 - ans) * 1.0 / (m - 1)) - 1;
if(i + step > n)//最后一步
{
ans += (n - i + 1) * m;
break;
}
ans += step * m;
i += step;
}
else ans = (ans + m) % i++;//否则正常递推
}
ans %= n;
}
printf("%d\n", ans + 1);
}
return 0;
} 这样写可能时间复杂度还是有点高，运行了1016ms。其实在此基础上还能再简——大概是运用到了整体思想吧，我也不是很清楚为什么能化到这一步……希望有大佬看了也能顺便教教我……
#include
using namespace std;
long long n, m, ans;
int t;
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%lld%lld", &n, &m);
ans = n * m;
while(ans > n)
ans = ans - n + (ans - n - 1) / (m - 1);
printf("%d\n", ans);
}
return 0;
} 这样的话时间也就近900ms，省了不少。核心一句，有很多看起来很眼熟的操作。（然而我还是没看懂QwQ）
三、特殊约瑟夫游戏
Description
YJC很喜欢玩游戏，今天他决定和朋友们玩约瑟夫游戏。约瑟夫游戏的规则是这样的：n个人围成一圈，从1号开始
依次报数，当报到m时，报1、2、...、m-1的人出局，下一个人接着从1开始报，保证(n-1)是(m-1)的倍数。最后剩
的一个人获胜。YJC很想赢得游戏，但他太笨了，他想让你帮他算出自己应该站在哪个位置上。
Input
第一行包含两个整数n和m，表示人数与数出的人数。
2≤m≤n<2^63-1 且(n-1)是(m-1)的倍数。
Output
输出一行，包含一个整数，表示站在几号位置上能获得胜利。
Sample Input
10 10Sample Output
10Sol
这个题的大意就是：每次有m - 1个人出去，求最后一人。看到数据范围就知道一定不能模拟了。但我们还是可以沿用之前求约瑟夫时找递推公式时的思维——
我们以一个例子为线索——当n = 22, m = 4的时候。手动模拟可以得出：最后活下来的人是8号。同样的，我们观察一下模拟过程（22个人里报4的那一圈省略，懒的画）
我们列举一些变量就更清晰了：
。看到第三列我分开步骤应该就可以明白一件事——每一轮活下去的人数为n / m + n % m。而后我们重新编号，是从上一轮后面的几个没有报数的人开始的，所以对于前面的所有数来说就相当于前面多了n % m个人，同时为m的倍数的人也少了，所以最后活下去的人的位置我们设为place，place从8到1，我们可以得到这么一个递推式子：
而我们需要的是逆推，移项易得，place从1到8的递推式子为：
值得注意的是，这里的n为当前递推到的那一轮的人数，而并非总共的人数。
不管n和m有多大，以这种方式进行，人数是大幅度锐减的，所以时间复杂度极低，系统反馈0ms。重点就在于推出来的公式。
下面就上代码啦~
#include
using namespace std;
typedef long long ll;
ll n, m;;
ll num[1 << 20];
int main()
{
scanf("%lld%lld", &n, &m);
ll tot = 1;
num[1] = n;
while(num[tot] != m)//等于m就是最后一轮，这里是在预处理递推要用到的人数n
{
tot++;
num[tot] = num[tot - 1] / m + num[tot - 1] % m;
}
ll place = 1;
for(int i = tot; i > 0; i--)//逆推
{
place = (place - (num[i] % m)) * m;
}
printf("%lld\n", place);
return 0;
} 四、反约瑟夫问题
所谓反约瑟夫，就是通过n和其他信息来求报的数m。
1.经典反~
Description
著名的约瑟夫问题是这样描述的：N个人排成一个圆圈，然后把这N个人按逆时针方向编号为1、2、…、N；随机产
生一个正整数M，然后从编号为1的人开始按逆时针计数，当某人计数为M的倍数时，该人出队；如此循环下去，直
到队列里只有一个人留下。你现在的任务是：对于输入文件的N和K，其中N为初始时约瑟夫圆圈中的人数，K为约瑟
夫问题中最后留下的人的编号；请你确定一个最小能发生这种结果的正整数M。
Input
为N和K，0＜N≤1000
Output
为最小的正整数M。
Sample Input
10 5Sample Output
2Sol
不要想还能有多简单，n<=1000这么小的范围想啥呢。直接枚举没毛病。
前文看懂了的人看代码应该一眼就懂了。
#include
using namespace std;
int n, k;
int num[1005];
bool check(int m)
{
for(int i = 2; i <= n; i++)
num[i] = (num[i - 1] + m) % i;//O(n)的递推，这里是不可能爆的
if(num[n] + 1 == k) return true;//毕竟是从0开始编号，所以要+1
return false;
}
int main()
{
scanf("%d%d", &n, &k);
if(k == n) puts("1");//当然可以直接处理！！！
else
{
for(int i = 1; ; i++)//不能设上界，不然就WA了
{
if(check(i))
{
printf("%d\n", i);
return 0;
}
}
}
} 这道题就是这样暴力最后也不过4ms，相当于给你个思路——怎么做反约瑟夫问题。
2.好人与坏人
Description
原始的Joseph问题的描述如下：有n个人围坐在一个圆桌周围，把这n个人依次编号为1，…，n。从编号是1的人开
始报数，数到第m个人出列，然后从出列的下一个人重新开始报数，数到第m个人又出列，…，如此反复直到所有的
人全部出列为止。比如当n=6，m=5的时候，出列的顺序依次是5，4，6，2，3，1。现在的问题是：假设有k个好人
和k个坏人。好人的编号的1到k，坏人的编号是k+1到2k。我们希望求出m的最小值，使得最先出列的k个人都是坏人
Input
只有一行就是k,0 < k < 14
Output
只有一行就是m
Sample Input
3Sample Output
5Sol
其实也就是在之前的经典反上加了一个条件——在n>k时，出圈的人的编号全部 > k。
当然k<14这么小的数据打表也是妥妥的。
#include
using namespace std;
int k, res = 0;
bool check(int m)
{
res = 0;
for(int i = 1; i <= k; i++)
{
res = (res + m - 1) % (k * 2 - i + 1);这里从1开始……我也不知道为什么从0开始就WA了
if(res < k) return false;
}
return true;
}
int main()
{
scanf("%d", &k);
for(int i = k; ; i++)//第一轮当然要直接保证>k啊~
{
if(check(i))
{
printf("%d\n", i);
return 0;
}
}
} 是的没错还是枚举。56ms。完全不会超。
3.本篇最难的一个非正常约瑟夫的题
Description
有编号从1到n的n个小朋友在玩一种出圈的游戏,编号为i+1的小朋友站在编号为i小朋友左边。编号为1的小朋友站
在编号为n的小朋友左边。首先编号为1的小朋友开始报数，接着站在左边的小朋友顺序报数，直到数到某个数字K
时就出圈。直到所有的小朋友都出圈，则游戏完毕。游戏过程如下图所示。
Input
第一行有一个正整数n, 2 <= n <= 20
第二行有n 个整数其中第i个整数表示编号为i 的小朋友第i个出圈。
Output
求最小的K，如果不存在，则输出一个单词“NIE”
Sample Input
4
1 4 2 3Sample Output
5Sol
看到有无解的情况就很明显不能枚举了。因为枚举我们无法确定上界，而且ans还极大。【n<=20，我也不知道怎么做到的。总之这道题就不是用正常的思维来做的。
就拿样例来说——1 4 2 3，可以得到依次出圈的序号为1 3 4 2。由每一个人在他出圈的那一轮中的序号和当时圈中的人数我们可以得到n - 1个同余方程：k % 当时人数 同余 当时出圈的人在这一轮中的编号。而同时解这n - 1个同余方程我们又需要运用到扩展中国剩余定理。这个问题就完了。【？！！！
可能你还没能很好的理解到，我们把样例的方程列出来就可以了：
就这样。【？？！！
咳咳看看代码吧。信息处理还是一个比较大的难点，后面就直接exCRT套路了。
#include
using namespace std;
int n;
int a[30], b[30], t[30], pos[30];
int exgcd(int a, int b, int &x, int &y)
{
if(!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int t = x;
x = y, y = t - a / b * y;
return d;
}
int mul(int a, int b, int p)//快乘
{
int ans = 0;
while(b)
{
if(b & 1) ans = (ans + a) % p;
a = (a + a) % p;
b >>= 1;
}
return ans;
}
int excrt()
{
int ans = b[1], M = a[1];
for(int i = 2; i < n; i++)
{
int x, y, B = ((b[i] - ans) % a[i] + a[i]) % a[i];
int gcd = exgcd(M, a[i], x, y);
if(B % gcd) return -1;//二元一次方程无解。
x = mul(x, B / gcd, a[i] / gcd);
ans += M * x;
M *= a[i] / gcd;
ans = (ans + M) % M;
}
return ans? ans : M;
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d",&t[i]), pos[t[i]] = i;
for(int i = 1;i < n; i++)
{
int now = pos[i], j = pos[i - 1];
while(j != now)//这里还是要简单模拟一下，因为直接pos相减的话存在中间有些人已经出去了。
{
j++;
if(j > n) j = 1;//圈
if(t[j] >= i) b[i]++;//b为最少数的数。判定j这个人还没有出去。
}
a[i] = n - i + 1; b[i] %= a[i];
}
int ans = excrt();
if(ans == -1) puts("NIE");
else printf("%d\n", ans);
} 以上就是约瑟夫集锦的全部内容啦！！真的不能小看约瑟夫问题啊！！
本篇有一个问题，希望有大佬能解答哇~~
迎评：）
——End——