费马小定理与欧拉定理

费马小定理

 假如p是质数，且gcd(a,p)=1，那么 a^(p-1)≡1（mod p）

欧拉定理 

 gcd(a,n)=1,则 a^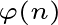≡1(mod p)

其中,是欧拉函数

欧拉定理证明

模m的同余类共有m个,分别为

它们构成m的完全剩余系

1-m中与m互质的数有个,它们构成m的简化剩余系

例如模10的简化剩余系为{},简化剩余系中任意两个乘起来还在简化剩余系中

例如7*9%10=3 , 3*7%10=1

因为若gcd(a,m)=gcd(b,m)=1,则gcd(a*b,m)=1

设n的简化剩余系为{a1,a2,...,a}

因为gcd(a,n)=1,所以a*a1,a*a2,...,a*a,可以表述n的简化剩余系

举个例子

3^=3^4≡1(mod 10)

3*1≡3(mod 10),3*3≡9(mod 10),3*7≡1(mod 10),3*9≡7(mod 10)

1,3,7,9又都出现了一边

所以

两边同除a1a2...an 得

所以,当p为质数时=p-1

a^(p-1)≡1(mod n),费马小定理显然成立

应用一段加强一下理解

原网址https://www.cnblogs.com/flipped/p/5218037.html

任意取一个质数，比如13。考虑从1到12的一系列整数1,2,3,4,5,6,7,8,9,10,11,12，给这些数都乘上一个与13互质的数，比如3，得到3,6,9,12,15,18,21,24,27,30,33,36。对于模13来说，这些数同余于3,6,9,12,2,5,8,11,1,4,7,10。这些余数实际上就是原来的1,2,3,4,5,6,7,8,9,10,11,12，只是顺序不同而已。

　　把1,2,3,„,12统统乘起来，乘积就是12的阶乘12！。把3,6,9,„,36也统统乘起来，并且提出公因子3，乘积就是312×12！。对于模13来说，这两个乘积都同余于1,2,3,„,12系列，尽管顺序不是一一对应，即312×12！≡12！mod 13。两边同时除以12！得312≡1 mod 13。如果用p代替13，用x代替3，就得到费马小定理

xp－1≡1 mod p。

 

我自己解释一遍(..•˘_˘•..)就是：

　　1*2*..*12 ≡ 3*6*9*12*2*5*8*11*1*4*7*10 mod 13 （因为顺序不同而已）

　　而3*6*9*12*15*18*21*24*27*30*33*36 ≡ 3*6*9*12*2*5*8*11*1*4*7*10 mod 13 （因为3和13互质，所以1，2，.. 12 乘上3后还是和13互质，12个数还是和1到12同余 ，只是顺序不同了 ）。

　　所以312×12！≡12！mod 13。

费马小定律可以快速求得x关于p的逆。前提是x与p互质。

x*xp-2 ≡1 mod p

所以xp-2就是x关于p的乘法逆元。