动态规划
53 Maximum Subarray 连续最大子数列
例如数组[1,-2,3,10,-4,7,2,-5]
//1.初始的cusum=1,sum=1,将-2加到cusum上得到-1,比1小,sum不更新。
//2.cusum小于0,更换为3,因为3比sum大,sum更新为3;
//3.cusum大于零,加10得13,13比sum大,sum更新为13.
依次按此方法,得到连续子数列最大值。
整理一下思路就是:
连续子数列的最大和是从一个候选数列中得到的,可以选这样一个候选数列:每一个标号结尾的最大数列,用cursum表示,cursum[i]表示以当前节点结尾的最大值,这个值可以通过遍历递进求得,如果之前的cursum[i-1]>0,那么cursum[i]=cursum[i-1]+a[i],如果cursum[i-1]<0,那么cursum[i]=a[i].(这里可以保证数列是连续的,以为并没有管当前的a[i]是否大于0,都做了加和)。这样就求出了cursum,sum只是保存cursum中最大的那个。
class Solution {
public:
int maxSubArray(vector& nums) {
int size=nums.size();
if(size==0) return 0;
int cursum=nums[0];
int sum=nums[0];
for(int i=1;i
class Solution {
public:
int maxSubArray(vector& nums) {
int size=nums.size();
if(size==0) return 0;
vector cursum(size,nums[0]);
for(int i=1;i 121 Best Time to Buy and Sell Stock40.9%Easy
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Example 1:
Input: [7, 1, 5, 3, 6, 4] Output: 5 max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price)思路:依次求出当前节点卖出时的股票收益curBenif,所以要求出之前的最小股票价格,用minStack表示。用benif表示最大的值。
class Solution {
public:
int maxProfit(vector& prices) {
int size=prices.size();
//前面处理开头准备工作
if(size<=1) return 0;
int sum=prices[1]-prices[0];
int cur=prices[1]-prices[0];
int minStock=prices[0]cur) cur=temp;
if(prices[i] 另外参考之前我写的 http://blog.csdn.net/m0_37693059/article/details/70291220
198 House Robber38.7%Easy
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
理解题意:相邻的房间不能都被偷,不是说一个房间的两侧不能被偷。
使用动态规划:题目简化为只有一个房间时的结果,然后依次增加后面的房间。假设前面已经求得了最好的结果。那么当考虑当前的房间时,当前的房间偷或者不偷。当选择到当前房间时,一个选择是:当前房间之前的房间不偷,偷当前的房间。另一个选择是,当前的房间不偷,则结果等于之前房间的结果。递推公式是:
dp[i]=max(dp[i-1],dp[i-2]+nums[i])
本题还需要考虑数列的大小,因为地推公式包含三个值,当数列只有一个,两个的时候要特殊处理。
class Solution {
public:
int rob(vector& nums) {
int size=nums.size();
if(size==0) return 0;
vector dp(size,nums[0]);
if(size==1) return dp[0];
dp[1]=nums[1]>nums[0]?nums[1]:dp[0];
if(size==2) return dp[1];
for(int i=2;itemp2?temp1:temp2;
}
return dp[size-1];
}
}; 第二种: 不需要设置一个矩阵class Solution {
public:
int rob(vector& nums) {
int n=nums.size();
int pre=0,cur=0;
for(int i=0;i 213. House Robber IINote: This is an extension of House Robber.
After robbing those houses on that street, the thief has found himself a new place for his thievery so that he will not get too much attention. This time, all houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, the security system for these houses remain the same as for those in the previous street.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
上题的变种,这道题改变的条件是,房子首尾连接成了一个圈。思路:分别假设第一个和最后一个房子没有偷,按照上题的解法求解,取两者的最大值
class Solution {
public:
int rob(vector& nums) {
int n=nums.size();
if(1==n) return nums[0];
return max(rob(nums,0,n-2),rob(nums,1,n-1));
}
//hos robber 1
int rob(vector& nums,int lo,int hi){
int pre=0,cur=0,temp=0;
for(int i=lo;i<=hi;i++)
{
temp=cur;
cur=max(nums[i]+pre,cur);
pre=temp;
}
return cur;
}
}; 91 Decode Ways19.5%Medium
class Solution {
public:
int numDecodings(string s) {
//注意输入的数可能不是1-9之间的数,这时跳过这个数不讨论
int size=s.size();
if(size==0) return 0;
vector dp(size,0);
if(s[0]>='1'&&s[0]<='9') dp[0]=1;
else return 0;
for(int i=1;i'9') return 0;
else if(s[i-1]=='1'||(s[i-1]=='2'&&s[i]<='6')) dp[i]=dp[i-1]+1;
else dp[i]=dp[i-1];
}
return dp[size-1];
}
}; 正确解法:
class Solution {
public:
int numDecodings(string s) {
//注意输入的数可能不是1-9之间的数,这时跳过这个数不讨论
int n=s.size();
if(!n) return 0;
vector res(n+1,0);
res[0]=1;//空字符串有一个
res[1]=(s[0]=='0'?0:1);
for(int i=2;i<=n;i++)
{
if(std::stoi(s.substr(i-1,1))!=0)
res[i]+=res[i-1];
//注意两个if是并列的,因为讨论的末尾不同,即使前面有相同的结果,考虑到最后末尾的不同,也是不同的结果,因此是加和
if(std::stoi(s.substr(i-2,2))>=10&&std::stoi(s.substr(i-2,2))<=26)
res[i]+=res[i-2];
}
return res[n];
}
}; 62 Unique Paths Medium 寻找所有的路径 简单的动态规划问题
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
![]()
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
思路:dp[i][j]=dp[i-1][j]+dp[i][j-1]
class Solution {
public:
int uniquePaths(int m, int n) {
vector> dp(m,vector(n,0));
if(m==0&&n==0) return 0;
dp[0][0]=1;
for(int i=0;i 63 Unique Paths II Medium 绝对路径2
class Solution {
public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
int m=obstacleGrid.size();
if(m==0) return 0;
int n=obstacleGrid[0].size();
if(n==0) return 0;
vector> dp(m,vector(n,0));
if(obstacleGrid[0][0]==1) return 0;//注意障碍可能是在入口处
dp[0][0]=1;
for(int i=0;i //这里最好是从1开始,因为当矩阵只有1个时,会出错64 Minimum Path SumMedium 最小路径和
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
一个矩阵包含一些数,要求找到从左上角到右下角和的最小值class Solution {
public:
int minPathSum(vector>& grid) {
int m=grid.size();
if(m==0) return 0;
int n=grid[0].size();
if(n==0) return 0;
vector> sum(m,vector(n,0));
sum[0][0]=grid[0][0];
for(int i=1;i 221 Maximal Square28.6%Medium
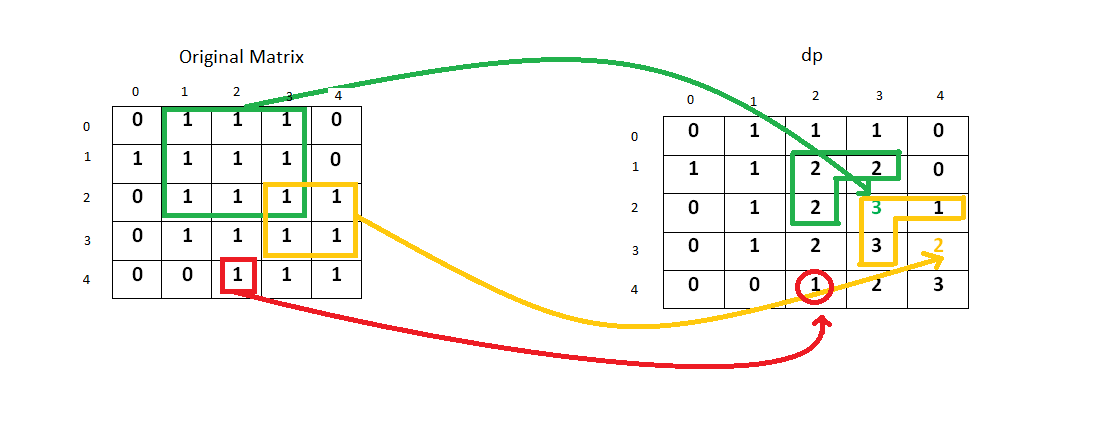
Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.
For example, given the following matrix:
1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0Return 4.
class Solution {
public:
int maximalSquare(vector>& matrix) {
int n=matrix.size();
if(!n) return 0;
int m=matrix[0].size();
int res=0;
vector> dp(n+1,vector(m+1,0));//技巧,多设置一排一列数组,就不需要考虑边界值的问题了
for(int i=1;i 改善,改善空间复杂度:
public class Solution {
public int maximalSquare(char[][] matrix) {
int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
int[] dp = new int[cols + 1];
int maxsqlen = 0, prev = 0;
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
int temp = dp[j];
if (matrix[i - 1][j - 1] == '1') {
dp[j] = Math.min(Math.min(dp[j - 1], prev), dp[j]) + 1;
maxsqlen = Math.max(maxsqlen, dp[j]);
} else {
dp[j] = 0;
}
prev = temp;
}
}
return maxsqlen * maxsqlen;
}
}85 Maximal Rectangle27.6%Hard
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.
For example, given the following matrix:
1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0Return 6.
152 Maximum Product Subarray25.5%Medium
Find the contiguous subarray within an array (containing at least one number) which has the largest product.
For example, given the array [2,3,-2,4],
the contiguous subarray [2,3] has the largest product = 6.
class Solution {
public:
int maxProduct(vector& nums) {
int result=std::numeric_limits::min();
int n=nums.size();
int front=1;
int back=1;
for(int i=0;i 大神解法2:动态规划
class Solution {
public:
int maxProduct(vector& nums) {
int result=std::numeric_limits::min();
int n=nums.size();
if(n==0) return 0;
result=nums[0];
for(int i=1,maxnum=result,minnum=result;i
120 Triangle 33.6% Medium 寻找三角形矩阵的最小路径
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
要求尽量少用额外空间
对于当前的节点triangle[i][j]只能走到triangle[i+1][j]或者triangle[i+1][j-1]。使用一维矩阵,随时更新。class Solution {
public:
int minimumTotal(vector>& triangle) {
int n=triangle.size();
if(n==0) return 0;
if(n==1) return triangle[0][0];
vector result(n,std::numeric_limits::max());//记住这种形式表示
result[0]=triangle[0][0];
for(int i=1;i=0;j--)
{
int tempMin=result[j];
if(j>0&&result[j-1] 139 Word Break29.7%Medium
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words. You may assume the dictionary does not contain duplicate words.
For example, given
s = "leetcode",
dict = ["leet", "code"].
Return true because "leetcode" can be segmented as "leet code".
UPDATE (2017/1/4):
The wordDict parameter had been changed to a list of strings (instead of a set of strings). Please reload the code definition to get the latest changes.
原题目的字典是set集合,这里把vector字典转换成set集合,空间复杂度增大。这里需要注意的是循环的下标和字符串的个数之间的关系。
class Solution {
public:
bool wordBreak(string s, vector& wordDict) {
int m=s.size();
int n=wordDict.size();
if(m==0||n==0) return false;
vector result(m+1,false);//这里字符串bool保存从0个字符串到m个字符串,这样的处理方式不需要特殊处理开始的部分。
unordered_set dic;
for(int i=0;i=0;j--)
{
if(result[j]&&dic.find(s.substr(j,i-j))!=dic.end())
{
result[i]=true;
break;
}
}
}
return result[m];
}
}; 300. Longest Increasing Subsequence
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example,
Given [10, 9, 2, 5, 3, 7, 101, 18],
The longest increasing subsequence is [2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.
Your algorithm should run in O(n2) complexity.
Follow up: Could you improve it to O(n log n) time complexity?
Credits:
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.
For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.
https://discuss.leetcode.com/topic/24255/summary-of-4-different-solutions-bfs-dp-static-dp-and-mathematics
class Solution {
public:
int numSquares(int n) {
if(n<=0) return 0;
static vector res={0};
while(res.size()<=n)
{
int size=res.size();
int least=std::numeric_limits::max();
for(int j=1;j*j<=size;j++)
{
least=min(least,res[size-j*j]+1);
}
res.push_back(least);
}
return res[n];
}
}; 96. Unique Binary Search Trees
Given n, how many structurally unique BST's (binary search trees) that store values 1...n?
For example,
Given n = 3, there are a total of 5 unique BST's.
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3 自己的思路:
class Solution {
public:
int numTrees(int n) {
if(!n) return 0;
vector res(n+1,0);
res[0]=1;
res[1]=1;
for(int i=2;i<=n;i++)
for(int j=1;j<=i;j++)
res[i]+=res[i-j]*res[j-1];
return res[n];
}
}; Given an integer n, generate all structurally unique BST's (binary search trees) that store values 1...n.
For example,
Given n = 3, your program should return all 5 unique BST's shown below.
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3 这道题在上一题的基础上,要求生成所有的树
class Solution {
public:
vector generateTrees(int n) {
vector> res(n+1);
res[0].emplace(nullptr);
res[1].emplace(TreeNode(1));
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
int left=j-1,right=i-j;
for(int lefti=0;leftileft= generateTrees(res,i,j-1,1,j,true);
head->right= generateTrees(res,i,i-j,j+1,j,false);
}
}
TreeNode* head=new TreeNode(j);
head->left= generateTrees(res,i,j-1,1,j,true);
head->right= generateTrees(res,i,i-j,j+1,j,false);
res[i].push_back(head);
// res[i]+=res[i-j]*res[j-1];
}
}
return res[n];
}
TreeNode* generateTrees(vector> &res,int i,int num,int minimal,int j,bool isleft){
//结果,当前行,子树节点数,节点中的最小值,头结点,是否是左子树
if(num==0) {
return nullptr;
};
int n=res[num].size();
for(int k=0;kleft=copyTrees(res,num,k,minimal-1);
else
head->right=copyTrees(res,num,k,minimal-1);
res[i].push_back(head);
}
}
TreeNode* copyTrees(vector> &res,int num,int k,int minimal){
if(num==0) return nullptr;
TreeNode* head=res[num][k];
return copyTrees(head,minimal);
}
TreeNode* copyTrees(TreeNode* head,int minimal){
if(head==nullptr) return nullptr;
TreeNode* newHead=new TreeNode(head->val+minimal);
if(head->left) newHead->left=copyTrees(head->left,minimal);
if(head->right) newHead->right=copyTrees(head->right,minimal);
return newHead;
}
}; 322. Coin Change 换钱的最小货币数
You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
Example 1:
coins = [1, 2, 5], amount = 11
return 3 (11 = 5 + 5 + 1)
Example 2:
coins = [2], amount = 3
return -1.
Note:
You may assume that you have an infinite number of each kind of coin.