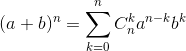组合数学 —— 组合数

【概念】

1.组合

从 n 个元素的集合 S 中，无序的选出 r 个元素，叫做 S 的一个 r 组合。

如果两个组合中，至少有一个元素不同，它们就被认为是不同的组合。

2.不可重组合数

所有不同组合的个数，叫做组合数，记作： 或 

由于每一种组合都可以扩展到 r！种排列，而总排列为 A(n,r) ，所以组合数

特别的，C(n,0)=1

3.可重复组合数

从 n 个不同的元素中，无序的选出 r 个元素组成一个组合，且允许这 r 个元素重复使用，则称这样的组合为可重复组合。

其组合数记为：

4.不相邻组合数

从 A={1,2,...,n} 中选取 m 个不相邻的组合，其组合数为：

例题：

① 一班有10名同学，二班有8名同学，现每个班级要选出2名学生参加一个座谈会，求有多少种选法？

根据组合数与乘法原理，共有：C(10,2)*C(8,2)=1260 种

② 某班有10名同学，有4名女同学，现要选出3名学生，其中至少有一名女同学，求有多少种选法？

根据组合数与加法原理，共有：C(4,1)*C(6,2)+C(4,2)*C(6,1)+C(4,3)*C(6,0)=60+36+4=100 种

【组合数常用公式】

1）

2）

3）

4）（二项式定理）

特殊展开：

5） 为奇数时有 n&m=n 

【求组合数的方法】

首先 C(n,m) 的值一定是自然数，因为连续 m 个自然数的积一定被 m! 整除，因此求 C(n,m) 的值关键在于如何避免做除法。

1.递归计算

利用公式  来递归的计算组合数

LL cal(LL n,LL k){
    if(n>n>>k;
    cout<

2.杨辉三角打表

利用公式 ，将计算 C(n,r) 的过程化为加法来做，由于二项式展开系数的与杨辉三角一致，故该方法的实质就是求杨辉三角第 n 行，第 r 列上的数。

int f[N][N];
int main()
{
    f[0][0]=1;
    for(int i=1;i<=N-1;i++)
        for(int j=1;j<=i+1;j++)
            f[i][j]=f[i-1][j]+f[i-1][j-1];

    int n,r;
    scanf("%d%d",&n,&r);
    printf("%d\n",f[n+1][r+1]);

    return 0;
}

3.公式化简打表

用 ，由于除以 m，因此相对没那么容易越界

int C[N];
void calculate(int n,int m){//C[i]即为C(n,i)的值
    C[0]=1;
    for(int i=1;i<=n;i++)
        C[i]=C[i-1]*(n-i+1)/i;
}

4.约分求重数

约分之后，分母即会变为 1，借此将除法化为乘法，约分方法是计算 1 到 n 之间的任意一个质数在 C(n,r) 的重数。

具体做法是对分子分母上的每个数分解质因子，用一个数组 C[] 来记录重数，若分子上的数分解一个质因子 p，则 C[p]++，反之若分母上的数分解出质因子 p，则 C[p]--，最后将每个质因子按其重数连乘即可。

将公式化为 ，通过直接计算质数 p 在 n! 中的重数而得到数组 C[]，质数 p 在自然数 n 中的重数是指自然数 n 的质因数分解式质数 p 出现的次数，质数 p 在 n! 的重数为： ，根据公式：，可以递推的求出 p 在 n！中的重数。

例如：72=2*2*2*3*3，质数 2 在 72 的重数是 3，质数 3 在 72 的重数是 2；n=1000，p=3时，有 1000 div 3+1000 div 9+1000 div 27+1000 div 81+1000 div 243+1000 div 729=333+111+37+12+4+1=498，因此 1000！能被 3^498 整除，但不能被 3^499 整除，使用递推公式后，有：333 div 3=111 ,111 div 3=37,37 div 3=12,12 div 3=4,4 div 3=1

程序实现时，先求出 1 到 n 间所有质数，再对每个质数求重数，从而计算从 n-r+1 到 n 的因子的重数与从 1 到 r 的因子的重数，前者减去后者，C[i] 中所存储的即为约分后质数因子的重数，再利用高精度加法，将答案存储，最后倒序输出即可。

#include
#include
#include
const int N=30000;
vector prime,C;
bool vis[N];
int res[10];
void Get_Prime()
{
    memset(vis,true,sizeof(vis));
    for(int i=2;i<=N;i++)
    {
        if(vis[i])
        {
            prime.push_back(i);//存储质数
            C.push_back(0);//当前质数的重数为0
            for(int j=i*i;j<=N;j+=i)//筛除所有以i为因子的数
                vis[j]=false;
        }
    }
}
void Add(int n,int p)//记录重数个数
{
    for(int i=0;in-r)//根据公式C(n,r)=C(n,n-r)简化计算
        r=n-r;

    for(int i=0;i=0;i--)
        printf("%d",res[i]);
    printf("\n");

    return 0;
}

【例题】

• Rooks（LightOJ-1005）(排列+组合)：点击这里
• Wall Painting（HDU-4810）(杨辉三角组合数打表+二进制枚举)：点击这里
• Combinations（POJ-1306）(公式化简法求组合数)：点击这里
• Binomial Showdown（POJ-2249）(公式化简法求组合数)：点击这里
• 集合的划分（信息学奥赛一本通-T1315）(递归法求组合数)：点击这里