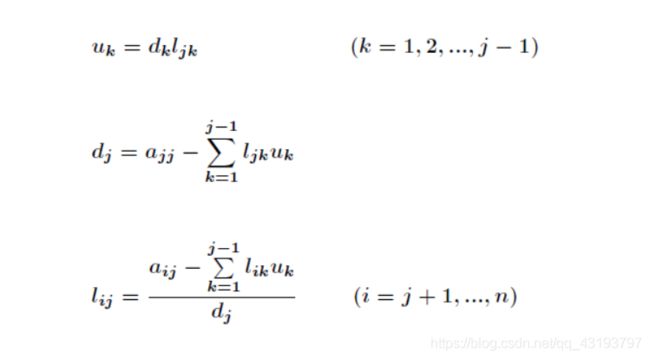Cholesky分解法
Cholesky分解法又叫平方根法，是求解对称正定线性方程组最常用的方法之一。对于一般矩阵，为了消除LU分
解的局限性和误差的过分积累，采用了选主元的方法，但对于对称正定矩阵而言，选主元是不必要的。
代码：
#include
#include
#include
#include
#include
using namespace std;
const int N = 1005;
typedef double Type;
Type A[N][N], L[N][N];
/** 分解A得到A = L * L^T */
void Cholesky(Type A[][N], Type L[][N], int n)
{
for(int k = 0; k < n; k++)
{
Type sum = 0;
for(int i = 0; i < k; i++)
sum += L[k][i] * L[k][i];
sum = A[k][k] - sum;
L[k][k] = sqrt(sum > 0 ? sum : 0);
for(int i = k + 1; i < n; i++)
{
sum = 0;
for(int j = 0; j < k; j++)
sum += L[i][j] * L[k][j];
L[i][k] = (A[i][k] - sum) / L[k][k];
}
for(int j = 0; j < k; j++)
L[j][k] = 0;
}
}
/** 回带过程 */
vector<Type> Solve(Type L[][N], vector<Type> X, int n)
{
/** LY = B => Y */
for(int k = 0; k < n; k++)
{
for(int i = 0; i < k; i++)
X[k] -= X[i] * L[k][i];
X[k] /= L[k][k];
}
/** L^TX = Y => X */
for(int k = n - 1; k >= 0; k--)
{
for(int i = k + 1; i < n; i++)
X[k] -= X[i] * L[i][k];
X[k] /= L[k][k];
}
return X;
}
void Print(Type L[][N], const vector<Type> B, int n)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
cout<<L[i][j]<<" ";
cout<<endl;
}
cout<<endl;
vector<Type> X = Solve(L, B, n);
vector<Type>::iterator it;
for(it = X.begin(); it != X.end(); it++)
cout<<*it<<" ";
cout<<endl;
}
int main()
{
int n;
cin>>n;
memset(L, 0, sizeof(L));
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
cin>>A[i][j];
}
vector<Type> B;
for(int i = 0; i < n; i++)
{
Type y;
cin>>y;
B.push_back(y);
}
Cholesky(A, L, n);
Print(L, B, n);
return 0;
}
/**data**
4
4 -2 4 2
-2 10 -2 -7
4 -2 8 4
2 -7 4 7
8 2 16 6
*/
代码：
#include
#include
#include
#include
#include
using namespace std;
const int N = 1005;
typedef double Type;
Type A[N][N], L[N][N], D[N][N];
/** 分解A得到A = LDL^T */
void Cholesky(Type A[][N], Type L[][N], Type D[][N], int n)
{
for(int k = 0; k < n; k++)
{
for(int i = 0; i < k; i++)
A[k][k] -= A[i][i] * A[k][i] * A[k][i];
for(int j = k + 1; j < n; j++)
{
for(int i = 0; i < k; i++)
A[j][k] -= A[j][i] * A[i][i] * A[k][i];
A[j][k] /= A[k][k];
}
}
memset(L, 0, sizeof(L));
memset(D, 0, sizeof(D));
for(int i = 0; i < n; i++)
{
D[i][i] = A[i][i];
L[i][i] = 1;
}
for(int i = 0; i < n; i++)
{
for(int j = 0; j < i; j++)
L[i][j] = A[i][j];
}
}
void Transposition(Type L[][N], int n)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < i; j++)
swap(L[i][j], L[j][i]);
}
}
void Multi(Type A[][N], Type B[][N], int n)
{
Type **C = new Type*[n];
for(int i = 0; i < n; i++)
C[i] = new Type[n];
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
C[i][j] = 0;
for(int k = 0; k < n; k++)
C[i][j] += A[i][k] * B[k][j];
}
}
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
B[i][j] = C[i][j];
}
for(int i = 0; i < n; i++)
{
delete[] C[i];
C[i] = NULL;
}
delete C;
C = NULL;
}
/** 回带过程 */
vector<Type> Solve(Type L[][N], Type D[][N], vector<Type> X, int n)
{
/** LY = B => Y */
for(int k = 0; k < n; k++)
{
for(int i = 0; i < k; i++)
X[k] -= X[i] * L[k][i];
X[k] /= L[k][k];
}
/** DL^TX = Y => X */
Transposition(L, n);
Multi(D, L, n);
for(int k = n - 1; k >= 0; k--)
{
for(int i = k + 1; i < n; i++)
X[k] -= X[i] * L[k][i];
X[k] /= L[k][k];
}
return X;
}
void Print(Type L[][N], Type D[][N], const vector<Type> B, int n)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
cout<<L[i][j]<<" ";
cout<<endl;
}
cout<<endl;
vector<Type> X = Solve(L, D, B, n);
vector<Type>::iterator it;
for(it = X.begin(); it != X.end(); it++)
cout<<*it<<" ";
cout<<endl;
}
int main()
{
int n;
cin>>n;
memset(L, 0, sizeof(L));
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
cin>>A[i][j];
}
vector<Type> B;
for(int i = 0; i < n; i++)
{
Type y;
cin>>y;
B.push_back(y);
}
Cholesky(A, L, D, n);
Print(L, D, B, n);
return 0;
}
/**data**
4
4 -2 4 2
-2 10 -2 -7
4 -2 8 4
2 -7 4 7
8 2 16 6
*/