JAVA算法：走方格的最小代价（走方格问题变形）

JAVA算法：走方格的最小代价（走方格问题变形）

给定一个矩阵（二维数组）和一个位置（m，n）。要求编写一个算法，返回从（0，0）到（m，n）的最小成本路径的成本。矩阵的每个单元格表示遍历该单元格的成本。到达路径的总成本（m，n）是该路径上所有成本（包括源和目标）的总和。在矩阵中移动时，只能从给定单元格向下、向右和斜向下方向（三个方向）遍历单元格，即从给定单元格（i，j）遍历单元格（i+1，j）、（i，j+1）和（i+1，j+1）。您可以假设所有成本都是正整数。

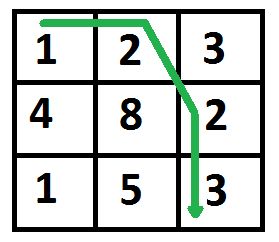
例如，在下图中，到（2，2）的最小成本路径是什么？

1	2	3
4	8	2
1	5	3

 

可以按照这个方法在矩阵中移动：从 (0, 0) –> (0, 1) –> (1, 2) –> (2, 2)。 最小成本路径成本值为： 8 (1 + 2 + 2 + 3).

最优子结构

到达（m，n）的路径必须通过三个单元之一：（m-1，n-1）或（m-1，n）或（m，n-1）。因此，最小到达成本（m，n）可以写为“3个单元的最小值加上成本[m][n]”。

最小成本（m，n）=min（最小成本（m-1，n-1），最小成本（m-1，n），最小成本（m，n-1））+成本[m][n]

重叠的子问题

下面是MCP（最小成本路径）问题的简单递归实现。实现只遵循上面提到的递归结构。

package com.bean.algorithm.basic;

public class MinCostPathInMatrix {

	/*
	 * A Naive recursive implementation of MCP(Minimum Cost Path) problem
	 * A utility function that returns minimum of 3 integers
	 */
	static int min(int x, int y, int z) {
		if (x < y)
			return (x < z) ? x : z;
		else
			return (y < z) ? y : z;
	}
	/*
	 * Returns cost of minimum cost path from (0,0) to (m, n) in mat[R][C]
	 */
	static int minCost(int cost[][], int m, int n) {
		if (n < 0 || m < 0)
			return Integer.MAX_VALUE;
		else if (m == 0 && n == 0)
			return cost[m][n];
		else
			return cost[m][n] + min(minCost(cost, m - 1, n - 1), minCost(cost, m - 1, n), minCost(cost, m, n - 1));
	}
	// Driver code
	public static void main(String args[]) {

		int cost[][] = { 
				{ 1, 2, 3 }, 
				{ 4, 8, 2 }, 
				{ 1, 5, 3 } 
				};

		System.out.print(minCost(cost, 2, 2));
	}
}

运行结果：

8

应该注意，上面的函数一次又一次地计算相同的子问题。参见下面的递归树，有许多节点不止一次出现。这种幼稚的递归解决方案的时间复杂度是指数级的，速度非常慢。

 算法设计（动态规划）

package com.bean.algorithm.basic;

public class MinCostPathInMatrix2 {

	/*
	 * Java program for Dynamic Programming implementation of Min Cost Path problem
	 * A utility function that returns minimum of 3 integers
	 */

	private static int min(int x, int y, int z) {
		if (x < y)
			return (x < z) ? x : z;
		else
			return (y < z) ? y : z;
	}

	private static int minCost(int cost[][], int m, int n) {
		int i, j;
		int tc[][] = new int[m + 1][n + 1];

		tc[0][0] = cost[0][0];

		/* Initialize first column of total cost(tc) array */
		for (i = 1; i <= m; i++)
			tc[i][0] = tc[i - 1][0] + cost[i][0];

		/* Initialize first row of tc array */
		for (j = 1; j <= n; j++)
			tc[0][j] = tc[0][j - 1] + cost[0][j];

		/* Construct rest of the tc array */
		for (i = 1; i <= m; i++)
			for (j = 1; j <= n; j++)
				tc[i][j] = min(tc[i - 1][j - 1], tc[i - 1][j], tc[i][j - 1]) + cost[i][j];

		return tc[m][n];
	}

	/* Driver program to test above functions */
	public static void main(String args[]) {
		int cost[][] = { 
				{ 1, 2, 3 }, 
				{ 4, 8, 2 }, 
				{ 1, 5, 3 } 
				};
		System.out.println(minCost(cost, 2, 2));
	}
}

运行结果：

8