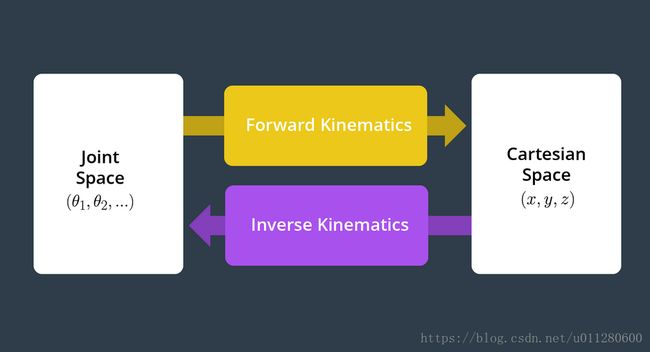
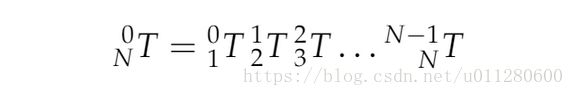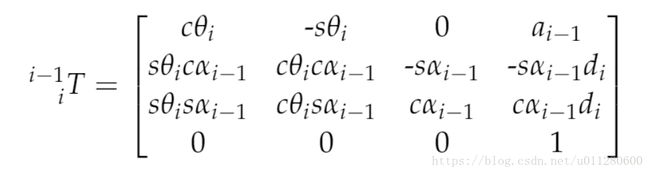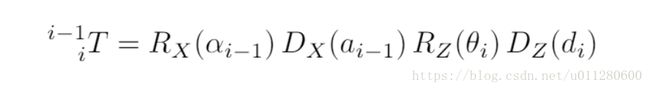正向运动学
串联机械手的正向运动学:
以前文提到的SCARA机器人为例,正向运动学代码实现如下:
from sympy import symbols, cos, sin, pi, simplify
from sympy.matrices import Matrix
### Create symbols for joint variables
q1, q2, q3, q4 = symbols('q1:5')
d1, d2, d3, d4 = symbols('d1:5')
a0, a1, a2, a3 = symbols('a0:4')
alpha0, alpha1, alpha2, alpha3 = symbols('alpha0:4')
a12 = 0.4500 # meters
a23 = 0.3000 # meters
# DH Parameters
s = {alpha0: 0, a0: 0, d1: 0,
alpha1: 0, a1: a12, d2: 0,
alpha2: 0, a2: a23, q3: 0,
alpha3: 0, a3: 0, d4: 0}
#### Homogeneous Transforms
T0_1 = Matrix([[ cos(q1), -sin(q1), 0, a0],
[ sin(q1)*cos(alpha0), cos(q1)*cos(alpha0), -sin(alpha0), -sin(alpha0)*d1],
[ sin(q1)*sin(alpha0), cos(q1)*sin(alpha0), cos(alpha0), cos(alpha0)*d1],
[ 0, 0, 0, 1]])
T0_1 = T0_1.subs(s)
T1_2 = Matrix([[ cos(q2), -sin(q2), 0, a1],
[ sin(q2)*cos(alpha1), cos(q2)*cos(alpha1), -sin(alpha1), -sin(alpha1)*d2],
[ sin(q2)*sin(alpha1), cos(q2)*sin(alpha1), cos(alpha1), cos(alpha1)*d2],
[ 0, 0, 0, 1]])
T1_2 = T1_2.subs(s)
T2_3 = Matrix([[ cos(q3), -sin(q3), 0, a2],
[ sin(q3)*cos(alpha2), cos(q3)*cos(alpha2), -sin(alpha2), -sin(alpha2)*d3],
[ sin(q3)*sin(alpha2), cos(q3)*sin(alpha2), cos(alpha2), cos(alpha2)*d3],
[ 0, 0, 0, 1]])
T2_3 = T2_3.subs(s)
T3_4 = Matrix([[ cos(q4), -sin(q4), 0, a3],
[ sin(q4)*cos(alpha3), cos(q4)*cos(alpha3), -sin(alpha3), -sin(alpha3)*d4],
[ sin(q4)*sin(alpha3), cos(q4)*sin(alpha3), cos(alpha3), cos(alpha3)*d4],
[ 0, 0, 0, 1]])
T3_4 = T3_4.subs(s)
# Transform from base link to end effector
T0_4 = simplify(T0_1 * T1_2 * T2_3 * T3_4)
print(T0_4)
print(T0_4.evalf(subs={q1: 0, q2: 0, d3: 0, q4: 0}))