【高等数学】导数与微分

本文为高等数学的学习笔记，讲解导数与微分。欢迎交流

导数概念

导数的定义

函数在一点处的导数

函数在 $x_0$ 处可导，取 $x_0$ 处的增量 $\Delta x$：
$$f^{\prime }(x_0)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$
或：
$$f^{\prime }(x_0)=\underset{x\to x_0}{\lim }\frac{f(x)-f(x_0)}{x-x_0}$$
可记作 $y^{\prime }{|}_{x=x_0},\frac{dy}{dx}{|}_{x=x_0}$ 或 $\frac{df(x)}{dx}{|}_{x=x_0}$。

单侧导数

由极限存在的充要条件有，可导的充要条件为左右极限都存在且相等：
$$\underset{h\to 0^{-}}{\lim }\frac{f(x_0+h)-f(x_0)}{x-x_0},\underset{h\to 0^{+}}{\lim }\frac{f(x_0+h)-f(x_0)}{x-x_0}$$
注意：判断导数在闭区间可导要考虑端点的情况

导数的应用

在点 $M(x_0,y_0)$ 处的切线方程为：
$$y-y_0=f^{\prime }(x_0)(x-x_0)$$
法线方程为：
$$y-y_0=-\frac{1}{f^{\prime }(x_0)}(x-x_0)$$

可导与连续性的关系

可导必连续，连续不一定可导。

函数的求导法则

商求导法则

$$(\frac{u}{v}{)}^{\prime }=\frac{u^{\prime }v-u{v}^{\prime }}{v^2}$$

反函数求导法则

若函数可导，则反函数也可导：
$$[f^{-1}(x){]}^{\prime }=\frac{1}{f^{\prime }(y)},\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}$$
反函数的导数=直接函数导数的倒数。

复合函数的求导法则

从内向外逐层求导：
$$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx},y^{\prime }(x)=f^{\prime }(u)g^{\prime }(x)$$

基本求导法则与导数公式

导数公式

$$(\tan x{)}^{\prime }={\sec }^{2}x(\cot x{)}^{\prime }=-{\csc }^{2}x$$

$$(\sec x{)}^{\prime }=\sec x\tan x(\csc x{)}^{\prime }=-\csc x\cot x$$

$$(a^x{)}^{\prime }=a^x\ln a({\log }_{a}x{)}^{\prime }=\frac{1}{x\ln a}$$

$$(\arcsin x{)}^{\prime }=\frac{1}{\sqrt{1-x^2}}(\arccos x{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}$$

$$(\arctan x{)}^{\prime }=\frac{1}{1+x^2}(\text{arccot}{)}^{\prime }=-\frac{1}{1+x^2}$$

高阶导数

初等函数的高阶导数：
$$(\sin x{)}^{(n)}=\sin (x+n\frac{\pi }{2})$$

$$(\cos x{)}^{(n)}=\sin (x+n\frac{\pi }{2})$$

$$[\ln (1+x){]}^{(n)}=(-1{)}^{n-1}\frac{(n-1)!}{(1+x{)}^n}$$

莱布尼兹公式：
$$(uv{)}^{(n)}=u^{(n)}v+n{u}^{(n-1)}{v}^{\prime }+\frac{n(n-1)}{2!}{u}^{n-2}{v}^{\prime \prime }+...$$

$$+\frac{n(n-1)...(n-k+1)}{k!}{u}^{(n-k)}{v}^{(k)}+u{v}^{(n)}$$

记忆技巧，按二项式定理展开：
$$(u+v{)}^n=u^n{v}^0+n{u}^{n-1}{v}^1+\frac{n(n-1)}{2!}{u}^{n-2}{v}^2+...+u^0{v}^n$$
即：
$$(u+v{)}^n=\sum _{k=0}^n{C}_n^k{u}^{n-k}{v}^k$$
将 $(u+v)$ 换为 $(uv)$，$k$ 次幂换为 $k$ 阶导数：
$$(uv{)}^n=\sum _{k=0}^n{C}_n^k{u}^{(n-k)}{v}^{(k)}$$

隐函数

隐函数的导数

将隐函数两边同时对 $x$ 求导，注意此时 $y$ 是 $x$ 的函数。

对数求导法：函数两边取对数，再求出 $y$ 的导数。当底数和指数都含有变量时，一般取对数进行处理。

参数方程确定的函数的导数

导数公式：
$$\frac{dy}{dx}=\frac{{\psi }^{\prime }(t)}{{\varphi }^{\prime }(t)}$$
二阶导数公式：
$$\frac{d^{2}y}{d{x}^2}=\frac{{\psi }^{\prime \prime }(t){\varphi }^{\prime }(t)-{\psi }^{\prime }(t){\varphi }^{\prime \prime }(t)}{{\varphi }^{\prime 3}(t)}$$

相关变化率

函数的微分

微分定义

可微的充要条件是可导，且微分为 $dy=f^{\prime }(x_0)\Delta x$

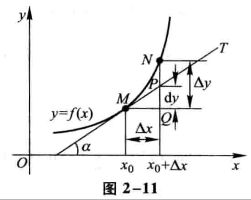
几何意义

基本初等函数的微分公式和微分运算法则

函数和差积商的微分法则

$$d(u\pm v)=du+dv$$

$$d(Cu)=Cdu$$

$$d(uv)=vdu+udv$$

$$d(\frac{u}{v})=\frac{vdu-udv}{v^2}$$

复合函数的微分法则

$$dy=f^{\prime }(u)du=f^{\prime }(u)g^{\prime }(x)dx$$

微分形式不变性：当变换自变量时，微分形式 $dy=f^{\prime }(u)du$ 不改变

微分在近似计算中的应用

略