LIS最长上升子序列详解（动态规划、贪心+二分、树状数组）

1.摘要：
关于LIS部分，本篇博客讲一下LIS的概念定义和理解，以及求LIS的三种方法，分别是O(n^2)的DP，O(nlogn)的二分+贪心法，以及O(nlogn)的树状数组优化的DP，最后附上几道非常经典的LIS的例题及分析。
2.LIS的定义：
最长上升子序列（Longest Increasing Subsequence），简称LIS，也有些情况求的是最长非降序子序列，二者区别就是序列中是否可以有相等的数。假设我们有一个序列 b i，当b1 < b2 < … < bS的时候，我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN)，我们也可以从中得到一些上升的子序列(ai1, ai2, …, aiK)，这里1 <= i1 < i2 < … < iK <= N，但必须按照从前到后的顺序。比如，对于序列(1, 7, 3, 5, 9, 4, 8)，我们就会得到一些上升的子序列，如(1, 7, 9), (3, 4, 8), (1, 3, 5, 8)等等，而这些子序列中最长的（如子序列(1, 3, 5, 8) ），它的长度为4，因此该序列的最长上升子序列长度为4。

首先需要知道，子串和子序列的概念，我们以字符子串和字符子序列为例，更为形象，也能顺带着理解字符的子串和子序列：
（1）字符子串指的是字符串中连续的n个字符，如abcdefg中，ab，cde，fg等都属于它的字串。
（2）字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符，即可以去掉字符串中的部分字符，但不可改变其前后顺序。如abcdefg中，acdg，bdf属于它的子序列，而bac，dbfg则不是，因为它们与字符串的字符顺序不一致。
知道了这个，数值的子序列就很好明白了，即用数组成的子序列。这样的话，最长上升子序列也很容易明白了，归根结底还是子序列，然后子序列中，按照上升顺序排列的最长的就是我们最长上升子序列了，这样听来是不是就很容易明白啦～
还有一个非常重要的问题：请大家用集合的观点来理解这些概念，子序列、公共子序列以及最长公共子序列都不唯一，但很显然，对于固定的数组，虽然LIS序列不一定唯一，但LIS的长度是唯一的。再拿我们刚刚举的栗子来讲，给出序列 ( 1, 7, 3, 5, 9, 4, 8)，易得最长上升子序列长度为4,这是确定的，但序列可以为 ( 1, 3, 5, 8 ), 也可以为 ( 1, 3, 5, 9 )。
3.LIS长度的求解方法：
那么这个到底该怎么求呢？
这里详细介绍一下求LIS的三种方法，分别是O(n^2)的DP，O(nlogn)的二分+贪心法，以及O(nlogn)的树状数组优化的DP。
解法1：动态规划：
我们都知道，动态规划的一个特点就是当前解可以由上一个阶段的解推出， 由此，把我们要求的问题简化成一个更小的子问题。子问题具有相同的求解方式，只不过是规模小了而已。最长上升子序列就符合这一特性。我们要求n个数的最长上升子序列，可以求前n-1个数的最长上升子序列，再跟第n个数进行判断。求前n-1个数的最长上升子序列，可以通过求前n-2个数的最长上升子序列……直到求前1个数的最长上升子序列，此时LIS当然为1。
　　让我们举个例子：求 2 7 1 5 6 4 3 8 9 的最长上升子序列。我们定义d(i) (i∈[1,n])来表示前i个数以A[i]结尾的最长上升子序列长度。
　　前1个数 d(1)=1 子序列为2；
　　前2个数 7前面有2小于7 d(2)=d(1)+1=2 子序列为2 7
　　前3个数 在1前面没有比1更小的，1自身组成长度为1的子序列 d(3)=1 子序列为1
　　前4个数 5前面有2小于5 d(4)=d(1)+1=2 子序列为2 5
　　前5个数 6前面有2 5小于6 d(5)=d(4)+1=3 子序列为2 5 6
　　前6个数 4前面有2小于4 d(6)=d(1)+1=2 子序列为2 4
　　前7个数 3前面有2小于3 d(3)=d(1)+1=2 子序列为2 3
　　前8个数 8前面有2 5 6小于8 d(8)=d(5)+1=4 子序列为2 5 6 8
　　前9个数 9前面有2 5 6 8小于9 d(9)=d(8)+1=5 子序列为2 5 6 8 9
　　d(i)=max{d(1),d(2),……,d(i)} 我们可以看出这9个数的LIS为d(9)=5
总结一下，d(i)就是找以A[i]结尾的，在A[i]之前的最长上升子序列+1，当A[i]之前没有比A[i]更小的数时，d(i)=1。所有的d(i)里面最大的那个就是最长上升子序列。其实说的通俗点，就是每次都向前找比它小的数和比它大的数的位置，将第一个比它大的替换掉，这样操作虽然LIS序列的具体数字可能会变，但是很明显LIS长度还是不变的，因为只是把数替换掉了，并没有改变增加或者减少长度。但是我们通过这种方式是无法求出最长上升子序列具体是什么的，这点和最长公共子序列不同。
状态设计：F [ i ] 代表以 A [ i ] 结尾的 LIS 的长度
状态转移：F [ i ] = max { F [ j ] + 1 ，F [ i ] } (1 <= j < i，A[ j ] < A[ i ])
边界处理：F [ i ] = 1 (1 <= i <= n)
时间复杂度：O (n^2)

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 103, INF = 0x7f7f7f7f;
int a[maxn], f[maxn];
int n,ans = -INF;
int main()
{
    scanf("%d", &n);
    for(int i=1; i<=n; i++) 
    {
        scanf("%d", &a[i]);

        f[i] = 1;
    }
    for(int i=1; i<=n; i++)
        for(int j=1; j<i; j++)
            if(a[j] < a[i])
                f[i] = max(f[i], f[j]+1);
    for(int i=1; i<=n; i++) 
        ans = max(ans, f[i]);
    printf("%d\n", ans);
    return 0;
}

解法2：贪心+二分：
思路：
新建一个 low 数组，low [ i ]表示长度为i的LIS结尾元素的最小值。对于一个上升子序列，显然其结尾元素越小，越有利于在后面接其他的元素，也就越可能变得更长。因此，我们只需要维护 low 数组，对于每一个a[ i ]，如果a[ i ] > low [当前最长的LIS长度]，就把 a [ i ]接到当前最长的LIS后面，即low [++当前最长的LIS长度] = a [ i ]。
那么，怎么维护 low 数组呢？
对于每一个a [ i ]，如果a [ i ]能接到 LIS 后面，就接上去；否则，就用 a [ i ] 去更新 low 数组。具体方法是，在low数组中找到第一个大于等于a [ i ]的元素low [ j ]，用a [ i ]去更新 low [ j ]。如果从头到尾扫一遍 low 数组的话，时间复杂度仍是O(n^2)。我们注意到 low 数组内部一定是单调不降的，所有我们可以二分 low 数组，找出第一个大于等于a[ i ]的元素。二分一次 low 数组的时间复杂度的O(logn)，所以总的时间复杂度是O(nlogn)。
　　我们再举一个例子：有以下序列A[ ] = 3 1 2 6 4 5 10 7，求LIS长度。
　　我们定义一个B[ i ]来储存可能的排序序列，len 为LIS长度。我们依次把A[ i ]有序地放进B[ i ]里。
（为了方便，i的范围就从1~n表示第i个数）
　　A[1] = 3，把3放进B[1]，此时B[1] = 3，此时len = 1，最小末尾是3
　 A[2] = 1，因为1比3小，所以可以把B[1]中的3替换为1，此时B[1] = 1，此时len = 1，最小末尾是1
　　A[3] = 2，2大于1，就把2放进B[2] = 2，此时B[ ]={1,2}，len = 2
　　同理，A[4]=6，把6放进B[3] = 6，B[ ]={1,2,6}，len = 3
　　A[5]=4，4在2和6之间，比6小，可以把B[3]替换为4，B[ ] = {1,2,4}，len = 3
　　A[6] = 5，B[4] = 5，B[ ] = {1,2,4,5}，len = 4
　　A[7] = 10，B[5] = 10，B[ ] = {1,2,4,5,10}，len = 5
　　A[8] = 7，7在5和10之间，比10小，可以把B[5]替换为7，B[ ] = {1,2,4,5,7}，len = 5
　　最终我们得出LIS长度为5。但是，但是！！这里的1 2 4 5 7很明显并不是正确的最长上升子序列。是的，B序列并不表示最长上升子序列，它只表示相应最长子序列长度的排好序的最小序列。这有什么用呢？我们最后一步7替换10并没有增加最长子序列的长度，而这一步的意义，在于记录最小序列，代表了一种“最可能性”。假如后面还有两个数据8和9，那么B[6]将更新为8，B[7]将更新为9，len就变为7，可以自行体会它的作用。
　　因为在B中插入的数据是有序的，不需要移动，只需要替换，所以可以用二分查找插入的位置，那么插入n个数的时间复杂度为〇(logn)，这样我们会把这个求LIS长度的算法复杂度降为了〇(nlogn)。

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn =300003, INF = 0x7f7f7f7f;
int low[maxn], a[maxn];
int n, ans;
int binary_search(int *a, int r, int x) 
/* int *a, 表示a变量是一个指针，用来接收main（）函数
调用时传来一个数组名，数组名代表数组元素的第一个元素
的地址。
low[binary_search(low, ans, a[i])] = a[i];
主函数调用时把low数组名传递过来，指针a接收数组名
也就是第一元素的地址，这样，在binary_search(int *a,
int r,int x）函数里用到a数组，就是主函数的
low数组。
*/
//二分查找，返回a数组中第一个>=x的位置 
{   int l = 1, mid;
    while(l <= r)
    {   mid = (l+r) >> 1;
        if(a[mid] <= x)
            l = mid + 1;
        else 
            r = mid - 1;
    }/*a[mid]<=x,说明大于x的数在mid的右侧，只要l<=r就一直
    循环下去，如果一直没有找到一个小于x的数会怎么样。例如
    10个数，mid=（1+10）/2=5,如果第5给数小于x，l=mid+1=6，
    下次循环处理第6到第10这几个数。mid=（6+10）/2=8，如果
    第8个数还是小于x，l=mid+1=9，下次循环就处理第9个数到第
    10个数，mid=（9+10）/2=9，如果第9个数还是小于x，
    l=mid+1=9+1=10，这是l=10等于r继续下次循环，l=11退出循
    环。实际上l=11是不可能的，因为在main（）中， if(a[i] >
     low[ans])  low[++ans] = a[i];  若a[i]>=low[ans]，直接
     把a[i]接到后面，小于在low[]数组中找小于x的值，也就是
     肯定能找到一个小于x的最小值。
       */    
 
    return l;
}
int main()
{   scanf("%d", &n);
    for(int i=1; i<=n; i++) 
    {   scanf("%d", &a[i]); 
        low[i] = INF;   //由于low中存的是最小值，所以low初始化为INF 
    }
    low[1] = a[1]; 
    ans = 1;   //初始时LIS长度为1 
    for(int i=2; i<=n; i++)
    {
        if(a[i] > low[ans])    //若a[i]>=low[ans]，直接把a[i]接到后面 
           low[++ans] = a[i];
        else       //否则，找到low中第一个>=a[i]的位置low[j]，用a[i]更新low[j] 
            low[binary_search(low, ans, a[i])] = a[i];
    }
    printf("%d\n", ans);   //输出答案 
    return 0;
}

解法3：树状数组维护

我们再来回顾O(n^2)DP的状态转移方程：F [ i ] = max { F [ j ] + 1 ，F [ i ] } (1 <= j < i，A[ j ] < A[ i ])

每次新拿一个a[i]的数，看一下这个数能不能为最大上升子序列长度做点贡献，所谓能做贡献就是新加入的a[i]这个数比前面的数要大，如果比前面所有的数都大，那就省事了，肯定f[i]=f[i-1]+1。如果不是这种情况，只能枚举1<=j

我们在递推F数组的时候，每次都要把F数组扫一遍求F[ j ]的最大值，时间开销比较大。我们可以借助数据结构来优化这个过程。用树状数组来维护F数组，首先把A数组从小到大排序，同时把A[ i ]在排序之前的序号记录下来。然后从小到大枚举A[ i ]，每次用树状数组中编号小于等于当前A[i]编号的元素的LIS长度+1来更新答案，同时把编号小于等于A[ i ]编号元素的LIS长度+1。因为A数组已经是有序的，所以可以直接更新。
注：把数从大到小排序，同时记录下原来所在的编号，每次取出一个数，这个数肯定大于前面的数，先取出数的序号，只要小于当前数的序号，那么当前取出的数的LIS，就是较小数LIS+1（当然先取出数的序号小于当前数的序号不止一个，选LIS最大的）

例如序列：3 1 2 6 4 5 10 7
把序列放到一个结构体中，同时记录它们的序号：
z[1].val=3 z[1].num=1
z[2].val=1 z[2].num=2
…
z[8].val=7 z[8].num=8
排序前 3 1 2 6 4 5 10 7
1 2 3 4 5 6 7 8（序号）
排序后 1 2 3 4 5 6 7 10
2 3 1 5 6 4 8 7（序号）
从小到大枚举排序后的序列，
int maxx=query(z[i].num);//查询编号小于等于num[i]的LIS最大长度
int query(int x)
{ int res=-INF;
for(;x;x-=x&(-x)) res=max(res,T[x]);
return res;
}
第一次调用maxx=query（z[1].num) maxx=query(2) z[1].val=1这个数排序之前的位置在第2位，所以找第2位之前的几个位置的最大LIS长度。
假如最大数10原来出现在第一位置，排序后最后处理它，但它的位置序号是1，小于1的序号没有，所有res=max（res，T[x]),返回值是0，用res+1来更新z[i].num。下面的两条语句就是这个作用
int maxx=query(z[i].num);//查询编号小于等于num[i]的LIS最大长度
modify(z[i].num,++maxx);//把长度+1，再去更新前面的LIS长度
我们发现原始序列最大数越排在最后，LIS越大。
上图：


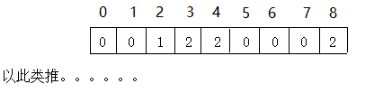
总结：树状数组不仅能维护前缀和，前缀和就是当前数前面所有数的和，还可以维护当前数前面所有数的最大值和最小值等。只不过树状数组查询和修改可以达到O（logn）
还有一点需要注意：树状数组求LIS不去重的话就变成了最长不下降子序列了。

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn =103,INF=0x7f7f7f7f;
struct Node{
    int val,num;
}z[maxn]; 
int T[maxn];//序号为i的LIS最大长度
int n;
bool cmp(Node a,Node b)
{
    return a.val==b.val?a.num<b.num:a.val<b.val;
}
void modify(int x,int y)
{
    for(;x<=n;x+=x&(-x)) T[x]=max(T[x],y);
}
int query(int x)
{
    int res=-INF;
    for(;x;x-=x&(-x)) res=max(res,T[x]);
    return res;
}
int main()
{
    int ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&z[i].val);
        z[i].num=i;
        /*z[i]这个结构体数组里有val和num两个成员变量，相当
        于有val[]和num[]两个数,为了注释方便，把z[i].val，
        z[i].num，在注释中记为val[]和num[],记住val[i]的编
        号，有点类似于离散化的处理，但没有去重 
        */
    }
    sort(z+1,z+n+1,cmp);//以权值为第一关键字从小到大排序 
    for(int i=1;i<=n;i++)//按权值从小到大枚举 
    {
        int maxx=query(z[i].num);//查询编号小于等于num[i]的LIS最大长度
        modify(z[i].num,++maxx);//把长度+1，再去更新前面的LIS长度
        ans=max(ans,maxx);//更新答案
    }
    printf("%d\n",ans);
    return 0;
}

树状数组第二种做法：
树状数组维护已经插入的元素中的LIS最大值。
有两个函数:
update(int x, int val):代表给把x这个位置的数变成val
qmax(int x):查询已经插入的数中小于x的最大值
具体的做法是:
f[i]:表示以a[i]结尾的LIS长度
对原序列进行离散化之后，对于每一个数，先查出小于这个数结尾的的LIS的最大值，那么f[i]= f[i] = qmax(a[i]) + 1;
然后再把以a[i]结尾的LIS的最大值f[i]插入到树状数组中。利用树状数组维护这一过程

#include 
using namespace std;
#define mem(a, b) memset(a, b, sizeof(a))
const int N = 1e5 + 10;
int a[N], b[N], c[N], n, len, f[N];
int lowbit(int x)
{
    return x & -x;
}
void update(int x, int val)
{
    for (int i = x; i <= n; i += lowbit(i))
        c[i] = max(c[i], val);
}
int qmax(int x)
{
    int ans = 0;
    for (int i = x; i; i -= lowbit(i))
        ans = max(ans, c[i]);
    return ans;
}
int main()
{
    //freopen("in.txt", "r", stdin);
    while (~scanf("%d", &n))
    {
        for (int i = 1; i <= n; i++)
            scanf("%d", &a[i]), b[i] = a[i];
        sort(b + 1, b + n + 1);
        len = unique(b + 1, b + n + 1) - b - 1;
        mem(c, 0);
        int ans = 0;
        for (int i = 1; i <= n; i++)
        {
            a[i] = lower_bound(b + 1, b + len + 1, a[i]) - b;
            f[i] = qmax(a[i]) + 1;
            update(a[i], f[i]);
            ans = max(ans, f[i]);
        }
        printf("%d\n", ans);
        //for (int i = 1; i <= n; i++)
        //    printf("%d\n", f[i]);
    }
    return 0;
}

树状数组第三种做法：
举一个简单的例子：
对于 1 4 2 3 5这个序列
显然他的LIS是4也就是 1 2 3 5
然后我们设 f[i]表示以a[i]结尾的LIS
有f[i]=max{f[j]+1 | j 首先我们先把1放入树状数组
发现1前并无数或者说f[0]=0;
则将f[1]赋值为f[0]+1=1，且树状数组中1位置赋值为1；

然后插入4
发现4前fmax=f[1]=1;
则将f[4]赋值为f[1]+1=2，且树状数组中4位置赋值为2；

然后插入2
发现2前fmax=f[1]=1;
则将f[2]赋值为f[1]+1=2，且树状数组中2位置赋值为2；

然后插入3
发现3前fmax=f[2]=2;
则将f[3]赋值为f[2]+1=3，且树状数组中3位置赋值为3；

然后插入5
发现5前fmax=f[3]=3;
则将f[5]赋值为f[3]+1=4，且树状数组中5位置赋值为4；

#include
using namespace std;
typedef long long ll;
int n,x,b[100100],a[100100];
ll c[100100],f[100100];
void upd(int x,ll v){
    for(;x<=n;x+=x&-x)
        c[x]=max(c[x],v);
}
ll ask(int x){
    ll cnt=0;
    for(;x>=1;x-=x&-x)
        cnt=max(cnt,c[x]);
    return cnt;
}

int main(){
    scanf("%d",&n);
    ll ans=0;
    memset(c,0,sizeof(c));
    for(int i=1;i<=n;i++){
        scanf("%d",&x);
        f[i]=ask(x)+1;
        upd(x,f[i]);
    }

    for(int i=1;i<=n;i++)
        ans=max(ans,f[i]);
    printf("%lld",ans);

    return 0;
}