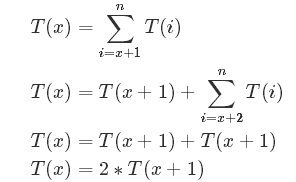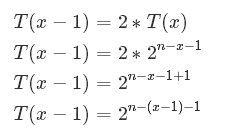Jump Game 搜索 动态规划 贪心
问题
给定一个非负整数数组,数组索引初始位置在数组的首元素位置处。数组中的每个元素值代表在这个位置可向前跳跃的最大长度(跳跃范围是[1,该位置的值])。当初始位置在数组首元素时判断是否可以到达数组的最后一个位置。
名词约定
如果我们在数组中的某个位置最终可到达最后一个位置,我们称这个位置为好位置。反之则称其为坏的位置。因此这个问题转化为数组的第一个位置是否是好位置?
解决方案
这是一个动态规划问题。一般,理解并完全解决一个动态规划问题分4步。
- 找出一个递归的回溯解决方案。
- 通过使用备忘录(通过一个数组记录每个子过程的结果,减少搜索步数)来优化1中的方法。(自顶向下的动态规划法)
- 消除递归(自底向上的动态规划)
- 应用一些技巧减少时间空间复杂度。
方法1.回溯法[栈溢出]
这种方法效率比较低,我们会尝试每个可能的跳跃步数看是否能到达终点,代码如下。
代码
public class Solution {
public boolean canJumpFromPosition(int position, int[] nums) {
if (position == nums.length - 1) {
return true;
}
int furthestJump = Math.min(position + nums[position], nums.length - 1);
for (int nextPosition = position + 1; nextPosition <= furthestJump; nextPosition++) {
if (canJumpFromPosition(nextPosition, nums)) {
return true;
}
}
return false;
}
public boolean canJump(int[] nums) {
return canJumpFromPosition(0, nums);
}
}上述代码的一种优化是,nextPosition的一次从大到小,在理论上这种方法最坏性能同没有优化前是一样的。但实际上,对于一般情况,该优化是能加快速度的。这种方法本质上是每次尝试最大跳跃步数,这样我们能尽快的到达终点。
代码优化部分如下。
// 从最小步数到最大步
for (int nextPosition = position + 1; nextPosition <= furthestJump; nextPosition++)
// 从最大数到最小步数
for (int nextPosition = furthestJump; nextPosition > position; nextPosition--)在下面的例子中,如果我们从位置0开始,跳到1,然后跳到6。这样0是一个好的位置。
Index 0 1 2 3 4 5 6
nums 1 5 2 1 0 2 0
下面是一个最坏情况的例子,优化后仍没有效果。但算法会搜索所有可能的情况,最终没有办法从任何位置跳到6。
Index 0 1 2 3 4 5 6
nums 5 4 3 2 1 0 0
按最大跳跃步数,跳跃步数列表为0 -> 4 -> 5 -> 4 -> 0 -> 3 -> 5 -> 3 -> 4 -> 5 -> etc.
复杂度分析
时间复杂度:O(2^n)。有2^n种方法从第一个位置跳到最后一个位置,n为数组长度。完整证明请看附录A。
空间复杂度:O(1),算法没有使用任何额外空间。
方法2(自顶向下动态规划)[栈溢出]
自顶向下动态规划可以看作是回溯法的一种优化。这依赖于,一旦我们确定了某个位置为好的位置或坏的位置,那么最终结果也就确定了。这意味着我们能够存储结果,并且不需要每次重新计算。
因此,对于数组中的每个位置,我们记录这个位置是好位置还是坏位置。我们通过数组memo来记录,值GOOD代表好的位置,BAD表示坏位置,UNKNOWN为不确定。这种方法被称为记忆法。
对于输入nums = [2, 4, 2, 1, 0, 2, 0],对应的memo数组如下。G代表GOOD,B代表BAD。可以看到我们无法从2,3,4位置到达位置6,但我们可以从0,1,5到达6。
Index 0 1 2 3 4 5 6
nums 2 4 2 1 0 2 0
memo G G B B B G G
算法步骤:
- 初始memo各个元素为UNKNOWN.最后一个位置被设置为GOOD。
- 修正方法1中的回溯法,搜索前先检查这个位置是GOOD还是BAD。
2.1. 如果GOOD或BAD则返回true或false
2.2如果是UNKNOWN则执行搜索。 - 一旦确定了当前位置是GOOD还是BAD我们将值存储在memo数组中。
代码
enum Index {
GOOD, BAD, UNKNOWN
}
public class Solution {
Index[] memo;
public boolean canJumpFromPosition(int position, int[] nums) {
if (memo[position] != Index.UNKNOWN) {
return memo[position] == Index.GOOD ? true : false;
}
int furthestJump = Math.min(position + nums[position], nums.length - 1);
for (int nextPosition = position + 1; nextPosition <= furthestJump; nextPosition++) {
if (canJumpFromPosition(nextPosition, nums)) {
memo[position] = Index.GOOD;
return true;
}
}
memo[position] = Index.BAD;
return false;
}
public boolean canJump(int[] nums) {
memo = new Index[nums.length];
for (int i = 0; i < memo.length; i++) {
memo[i] = Index.UNKNOWN;
}
memo[memo.length - 1] = Index.GOOD;
return canJumpFromPosition(0, nums);
}
}复杂度分析
时间复杂度:O(n^2),对于数组中的每个元素i,都会去寻找下一个位置nums[i],以找到一个好的位置。nums[i]最大为n,n为数组nums的长度。
空间复杂度:O(n)。
方法3 动态规划 自底向上 [超时]
自顶向下到自底向上版本是通过消除递归来完成。实际上,由于不存在方法栈的开销及通过缓存某些阶段的结果,获得较好的性能。此外通过递推来消除递归。
代码
enum Index {
GOOD, BAD, UNKNOWN
}
public class Solution {
public boolean canJump(int[] nums) {
Index[] memo = new Index[nums.length];
for (int i = 0; i < memo.length; i++) {
memo[i] = Index.UNKNOWN;
}
memo[memo.length - 1] = Index.GOOD;
for (int i = nums.length - 2; i >= 0; i--) {
int furthestJump = Math.min(i + nums[i], nums.length - 1);
for (int j = i + 1; j <= furthestJump; j++) {
if (memo[j] == Index.GOOD) {
memo[i] = Index.GOOD;
break;
}
}
}
return memo[0] == Index.GOOD;
}
}
复杂度分析
时间复杂度:O(n^2)
空间复杂度:O(n)
方法4,贪心法[AC]
从右向左迭代,在某个位置上,如果当前位置 + 可跳跃步数 >= 最近一个好位置,那么这个位置也是一个好位置。
从右向左迭代,检查每个位置,看这个位置是否是能够跳跃到好的位置(currPosition + nums[currPosition] >= leftmostGooodIndex).如果能够跳到好的位置,那么这个位置本身也是一个好的位置。因此这个位置是最新找到的一个好的位置,即最左的一个好位置。继续迭代,直到到达数组首元素。如果第一个位置是一个好位置,那么我们就从第一个位置跳
到最后一个位置。
下面通过表格来描述算法,对于数组nums = [9, 4, 2, 1, 0, 2, 0].G代表GOOD,B代表BAD,U代表UNKNOWN。假定已经走到位置1,1为G,可以从1跳到6。而nums[0] = 9,那么一定能够跳到1,因此最终可以从0号位置跳到最后一个位置。
Index 0 1 2 3 4 5 6
nums 9 4 2 1 0 2 0
memo U G B B B G G
代码
public class Solution {
public boolean canJump(int[] nums) {
int lastPos = nums.length - 1;
for (int i = nums.length - 1; i >= 0; i--) {
if (i + nums[i] >= lastPos) {
lastPos = i;
}
}
return lastPos == 0;
}
}
复杂度分析
空间复杂度:O(n)
时间复杂度:O(1)
附录A:方法1的复杂度分析
方法1中从第一个位置跳到最后一个位置有2^n中方法,n是数组长度。方法一是通过递归的方式完成。令T(X)为从位置x跳到位置n所用的步数。
T(n)=1, ![]()
因为从x到n等于分别以x+1到n为起点,到最后一个位置n的步数总和。
T(x) = 2*T(x+1) = 2*2*T(x+2) = 2*2*2*T(x+3) 括号内的表达式为n时候其结果为1。而对于x+1位置距离n为n-x-1。
因此令T(x) = 2^n-x-1,证明T(x-1) = 2^n-(x-1)-1。
T(1) = 2^n-2,所以时间复杂度为O(2^n)。
原文地址:
https://leetcode.com/articles/jump-game/