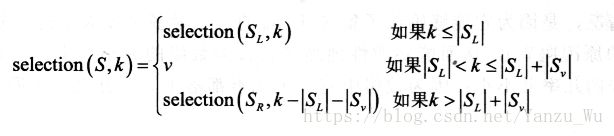算法分析与设计 第二周
算法分析与设计
寻找第K大数
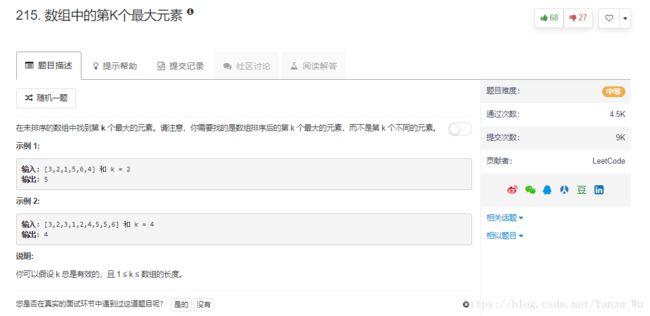
题目描述
选题原因
本周学习了分治算法,在学习中出现了例题
寻找第K大数字,以往的做法通常是维护一个长度为k的数组,保存最大的k个数,扫描所有的值,不断地加入数组。而新的分治算法则有着极低的复杂度。恰巧本题是中等难度,因此选择使用两种解法分别解题并做比较。
维护长度为K数组
解题思路
维持长度为k的数组,以及两个变量
minminpos,记录当前数组中最小的数字及最小数所在的位置。当有数字大过最小数,则替换最小数,并且扫描整个数组,更新最小数。
解题过程
int findKthLargest(vector<int>& nums, int k) {
int temp[k];
//初始化数组
for (int i = 0; i < k; i++) {
temp[i] = -1;
}
int min = -1;
int minindex = 0;
vector<int>::iterator it = nums.begin();
//遍历数组
for ( ; it != nums.end(); it++) {
//如果有数字大于最小数,加入数组
if (*it > min) {
temp[minindex] = *it;
min = *it;
//更新数组中的最小数
for (int i = 0; i < k; i++) {
if (temp[i] < min) {
min = temp[i];
minindex = i;
}
}
}
}
return temp[minindex];
}分治算法
解题思路及过程
原始算法
每次挑选一个中间数
x(首先选择k - 1),并维护三个数组,leftrightv,若数字大于x,则放入right;若数字小于x,则放入left;否则放入v。再根据情况递归。递归规则如下:
图中是找第k小数规则,只需要将他稍微颠倒一下即可。算法如下:
int findKthLargest(vector<int>& nums, int k) {
int comp = nums[k - 1];
vector<int>::iterator it = nums.begin();
vector<int> left;
vector<int> right;
vector<int> v;
//为所有数字分组
for ( ; it != nums.end(); it++) {
if (*it > comp) {
right.push_back(*it);
} else if (*it < comp) {
left.push_back(*it);
} else {
v.push_back(*it);
}
}
//选择需要递归的数组
if (k <= right.size()) {
//在右边
return findKthLargest(right, k);
} else if (k > right.size() && k <= right.size() + v.size()) {
//已选中
return v.front();
} else {
//在左边
return findKthLargest(left, k - right.size() - v.size());
}
}
优化取中间值
结果发现超出了内存限制,算法需要改进,首先修改中间数
x的取值,当长度小于20时,取nums的中间数,为了保险,选择两个数取平均值(如果只取一个数可能取到最小数,因此取中间两个数,作为调节)
int max = nums.size(); //总长
int comp = 0;
if (max > 20) {
comp = (nums[max/2] + nums[max/2 + 1]) / 2;
} else {
comp = nums[max/2];
}通过测试,不妨修改一个简单的参数,当长度小于
5时,就用心的方法取中间值x,再次测试。
发现算法反而变差了,那我们不妨试着当长度大于
10时则取值,再次测试。
发现算法与
20时差不多。
优化内存占用
之前算法失败的原因是占用太多内存,虽然在此基础上使空间占用稍小了一些,但实际上还有别的方法可以优化更多。
观察后发现,实际上,每次分类之后我们只会用到一个分组,则另外一个分组实际上是不需要放入那么多数字的。实际上,vector是很占用空间的。
我们发现,当右边个数 >= k时,则只会用到右边,此时就不必向左边数组插入元素;同理,当leftnum >= max - k,则只需要用到左边。
因此,我们使用两个变量标记useleftuseright,每次插入前判断。
int findKthLargest(vector<int>& nums, int k) {
int max = nums.size(); //总长
int comp = 0;
if (max > 20) {
comp = (nums[max/2] + nums[max/2 + 1]) / 2;
} else {
comp = nums[max/2];
}
vector<int>::iterator it = nums.begin();
bool useleft = false; //结果只需要left,不需要向right和v添加
bool useright = false; //结果只需要right,不需要向left和v添加
int leftnum = 0; //实际left应该有的数量,下同
int rightnum = 0;
int vnum = 0;
vector<int> left;
vector<int> right;
vector<int> v;
//为所有数字分组
for ( ; it != nums.end(); it++) {
if (*it > comp) {
//当只用到左边的时候,则不需要实际插入
if (!useleft) {
right.push_back(*it);
}
//需要计数,之后用到
rightnum++;
//判断此时是否只用得到
if (rightnum >= k) {
useright = true;
}
} else if (*it < comp) {
if (!useright) {
left.push_back(*it);
}
leftnum++;
if(leftnum >= max - k) {
useleft = true;
}
} else {
v.push_back(*it);
vnum++;
}
}
//选择需要递归的数组
if (k <= rightnum) {
//在右边
return findKthLargest(right, k);
} else if (k > rightnum && k <= rightnum + vnum) {
//已选中
return v.front();
} else {
//在左边
return findKthLargest(left, k - rightnum - vnum);
}
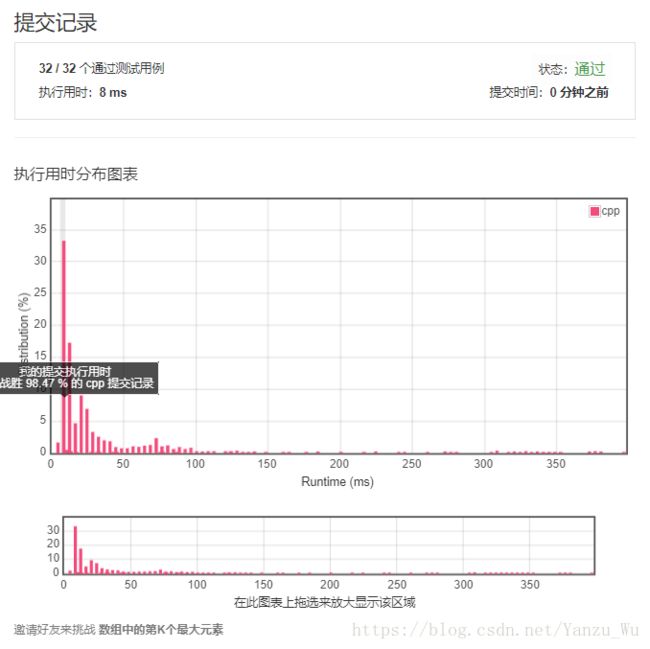
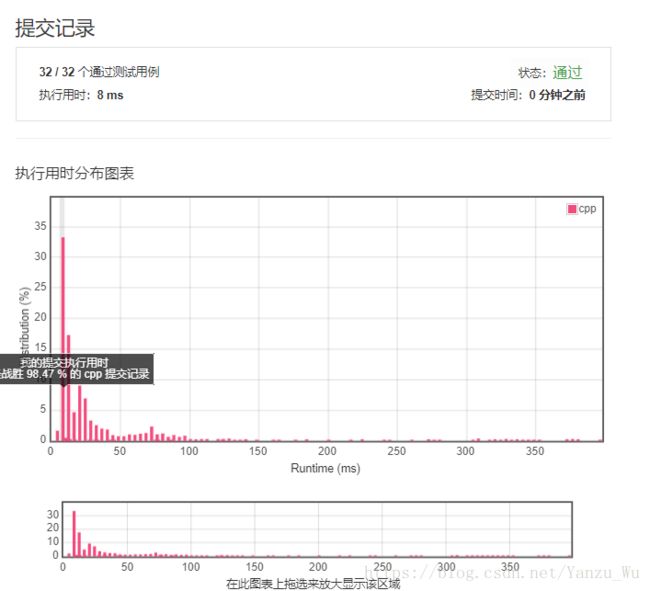
}发现虽然速度上没有什么实际的变化,但是对于空间的损耗的确少了许多。
源代码
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int max = nums.size(); //总长
int comp = 0;
if (max > 20) {
comp = (nums[max/2] + nums[max/2 + 1]) / 2;
} else {
comp = nums[max/2];
}
vector<int>::iterator it = nums.begin();
bool useleft = false; //结果只需要left,不需要向right和v添加
bool useright = false; //结果只需要right,不需要向left和v添加
int leftnum = 0; //实际left应该有的数量,下同
int rightnum = 0;
int vnum = 0;
vector<int> left;
vector<int> right;
vector<int> v;
//为所有数字分组
for ( ; it != nums.end(); it++) {
if (*it > comp) {
//当只用到左边的时候,则不需要实际插入
if (!useleft) {
right.push_back(*it);
}
//需要计数,之后用到
rightnum++;
//判断此时是否只用得到
if (rightnum >= k) {
useright = true;
}
} else if (*it < comp) {
if (!useright) {
left.push_back(*it);
}
leftnum++;
if(leftnum >= max - k) {
useleft = true;
}
} else {
v.push_back(*it);
vnum++;
}
}
//选择需要递归的数组
if (k <= rightnum) {
//在右边
return findKthLargest(right, k);
} else if (k > rightnum && k <= rightnum + vnum) {
//已选中
return v.front();
} else {
//在左边
return findKthLargest(left, k - rightnum - vnum);
}
}
};