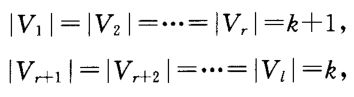《图论及其应用》学习笔记（图和简单图）

图和简单图：

一个图就是，由一个表示具体事物的点的集合，和表示事物之间联系的一些线的集合所构成。

平凡图：只有一个点而无边的图。

空图：边集为空的图。

假设u和v是e的端点，称u与e相关联。

 

图的同构：

且和的重数相同。

等价类：按照同构关系可划分。

商集：所有等价类为元素构成的集合。

 

完全偶图：具有二分类（X,Y）的简单偶图，其中X的每个顶点与Y的每个顶点相连。

补图：

对于一个简单图G=(V,E)，令集合，则图称为G的补图。

ps：这里E和E1的边加起来，就是完全图的边数。

ps：因为是自补图，自己和自己的补图同构，边数当然是一样的啦。

取模运算，商偏向于负无穷方向。去余运算，商偏向于0方向。

a ≡ b (mod p)，表明a和b对p取模，它们余数相等。

 

顶点的度，度序列：

奇点：奇数度的顶点；偶点：偶数度的顶点。

k正则图：每个点的度数都为k。如：完全图和完全偶图均是正则图。

握手定理：

 

ps：因为总的度数为偶数。偶点无论怎么加都为偶数，奇点要加够偶数个，才为偶数。

ps：k为奇数，则图的所有点都为奇点，奇点的个数必为偶数，也就是阶数为偶数。

 

ps：当△（G）＜n-1时， 所有的度可能的情况都在括号里了。当△（G）=n-1时，每个顶点的度数范围在最小度到最大度之间，这个长度的范围是，又有△（G）+1=n，减去δ就肯定＜n了，那肯定有顶点重复。

 

子图与图的运算：

子图：顶点集是子集、边集也是子集，而且子图中的边的重数不超过G中对应边的重数。

生成子图：顶点集相同的子图。

导出子图：提取出一个顶点集，和这些顶点集相关联的边的子图。

相关记法：G[V']；G[V\V']是除去V'顶点及相关联的边，也有G-V’

边导出子图：提取出边集，和这些边的端点，的子图。

相关记法：G[E']；G[E\E']，也有G-E'

并图：G1∪G2，顶点集和边集都要并，也记为G1+G2。

交图：G1  G2，至少要有一个公共顶点。

差：G1-G2，由G1中去掉G2中的边组成的图。

对称差：

 

联图：G1和G2不能相交，把G1的每个顶点和G2的每个顶点连接起来，记为G1VG2。

K1VK2=K5，K2VK3=K5

积图：对顶点集V=V1 X V2，得到u=(u1,u2)，v=(v1,v2)

若u1=v1，u2和v2在原图中邻接，或者u2=v2，u1和v1在原图中邻接，则u和v连线。

G=G1 X G2

运算后，点和边的数目统计：

ps：积图边的数目，G1顶点数n1要和G2的顶点数n2做积，因此n1每个点要负责m2条边的连接。

 

路与图的连通性：

迹：途径中的边，互不相同。

路：途径是迹，且顶点也互不相同。

连通是顶点集V上的一个等价关系，可将V划分为一些等价类。

可得，连通分支的概念，连通分支个数，记为(G)，连通图 (G)=1。

ps：通过证明任意两点都是连通的方式，来证明G的补图是连通图。

闭迹：称为回路。

圈：起点与内部顶点互不相同。长为k的圈称为k圈；根据k是奇数还是偶数，则称k圈是奇圈和偶圈。

直径：一个图中，最长的距离。

ps：在必要性的证明中，圈的长度为k-1，当k为奇数时，则圈就为偶圈。

在充分性的证明中，先根据距离的奇偶性划分为两个集合X和Y，再证明（X,Y）是个二分类，即它们集合内部，任意两点都不相连。具有相同奇偶性的数相加，必为偶数。

 

最短路及其算法：

Dantijg算法（顶点标号法）：

ps: Ti为a1到ai的最短路上的边集合；Ai为已经标号的顶点集合；t(an)表示an的标号值，a1到an的最短路长度。

步骤2做的事情：

遍历每个已标号顶点an。找出：某个已标号顶点an的，未标号邻点。然后算出：某个已标号顶点an，到其最近邻点距离。不但要找出l最小，还要使得步骤3中的，t+l最小。

步骤3做的事情：

可以得出某个已标号顶点使得，根据步骤2，算出的各个最小值中，再找出最小值，然后做相应的更新。

好的图论算法：若在如何一个具有m条边的n阶图G上，实施这个算法所需要的计算步数，都可由n和m的一个多项式为其上界。

动态规划是Bellman，作为多阶段决策过程而研究出来的。

 

图的代数表示及其特征：

邻接矩阵：若节点间相邻，则为1，否则为0；

ps：推论1中，自身到自身，有两个方向可走。因此，可得出度数和三角形数目的两倍。

关联矩阵：

某点vi与边ej有关联时，则，否则为0。

 

极图：

l部图：将点集V划分为l个互不相交的集合，且每个集合内的点，互不相连。

l=2时，G为偶图；n阶图必为n部图。

若，因此，部图也是部图。

ps：个集合里的任一个集合都是互不相连的，因此，可任选一些集合来继续划分至，集合数量达到。

完全l部图：每个集合内的点，都和其它集合里的点，均有边相连。

完全l部图可表示为：

它显然有：和条边。

n阶完全l几乎等部图：

对于一个n个点的完全l部图G中：

有：，因为，k(l-r)+r(k+1)=kl+r的形式。

所以记为：

ps:若u的选取，在V1中，则v要经过V2中的点，才能到达u。

ps：当n1=n2=n/2时，能使m=n1*n2达到最大。

 ps:若是要边数最多，则必定要是个完全l部图，完全l几乎等部图意味着每个集合的元素个数接近相等，若每个集合里元素相等，则必定是完全l几乎等部图。

 

H的度序列优于G，或者是，G的度序列弱于H，表示的是：有一个映射μ，使得G中的任何点u，有关系成立。

ps：若G度弱于H，一定有：m(G)≤m(H)。

   

 ps：先取出最大度的那个顶点u，再取出u的所有的邻接点的导出子图G1。G1要是含有，则 u V G1，就是了。

V2应包含u点，则G2VG1的边数不少于G。

ps：只能导出G1这么多个顶点，之后，通过v点能导出更多个顶点。

因为G度弱于，度弱于，而G和H有相同的度序列，则G和有相同的度序列。

因为中，V1每个点和V2每个点相连，G和有相同的度序列，那在G中，V1和V2肯定也是互相的。

和有相同的度序列，G1和H1连接G2中的点的边数是一样的，因此G1和H1的度序列也必须是相等。

归纳假设是：G1不含，且度弱于完全t-1部图H1，且G1与H1有相同的度序列，则同构；

因此推导出，做联图后，和也同构。

 

托兰定理：

ps：定理18说明，完全l部图的边数肯定 ≤ 完全l几乎等部图。

 

托兰定理的应用：

排雷模型：在任意的两个人之间的距离不超过g米的条件下，距离大于等于h米的人数对最多能达到多少对。

平面点集A的直径：指A中点对的距离的最大值，其中距离是指欧式距离。

建立模型：计算在直径为g的点集中最多有多少点对，其距离大于h。