等比数列三角形 （数论 + 黄金分割点）+ JOISC 2016 Day3 T3 「电报」（基环树 + 拓扑排序）

T1：等比数列三角形

题目

求三边都是 ≤n 的整数，且成等比数列的三角形个数
注意三角形面积不能为 0
注意 oeis 中未收录此数列，所以并不需要去搜了

输入格式
一行一个整数 n
输出格式
一行一个整数表示答案

样例
样例输入1
9
样例输出1
10
样例解释1
除去 9 个等边三角形，还有 {4，6，9} 。

样例输入2
100
样例输出2
133

数据范围与提示
一共有 4 个子任务，对于每一个子任务，你只有通过了该子任务的所有测试点，才能获得此子任务的分数
有 10pts，保证 n≤10
有 20pts，保证 n≤10⁵
有 20pts，保证 n≤10⁵
有 50pts，保证 n≤10¹²
对于所有数据，有1≤ n≤10¹²

题解

注意{4,6,9}，{6,4,9}，{9,6,4}算同一个三角形，所以不用管顺序
设三条边从小到大分别为$a,ak,a{k}^2$($k$为公比且为正整数)
所以$1\le k$

---

就然要构成三角形，必然要满足
$a+ak>a{k}^2=>1+k>k^2=>k^2-k-1<0$
解得$k<\frac{\surd 5+1}{2}$

综上$k\in [1,\frac{\surd 5+1}{2})$

---

接下来令$k=\frac{p}{q}$(q,p互质)，最大边就表示为$a\ast \frac{p^2}{q^2}$，最大边≤n，故此$q\le \surd n$
因为$q=\frac{p}{k}$，那么
1.当k取最大时，q取最小，把$k=\frac{\surd 5+1}{2}$带入就解出了q的最小值，
但因为k取不到这个开区间，q的这个最小值也是一个开区间
2.当k取最小时，q取最大，这是满足$q=p$，q的这个最大值是一个闭区间

综上$q\in (p\ast \frac{2}{\surd 5+1},p]$，在这里有个转化思想，把p代换成q，得到$q\in (q\ast \frac{2}{\surd 5+1},q]$
我们就可以枚举$p\in [1,\surd n]$，算出此时q的可取值个数，注意：其实理解成枚举q也是说得通的

---

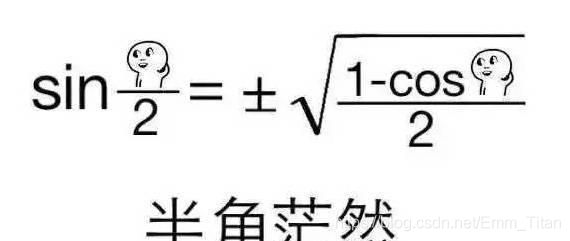
当这样统计完后，会出现一个问题
{2，3，6}，{4，6，9}这种公比为$\frac{3}{2}$的三角形，会被重复计算进公比为$\frac{6}{4}$
所以我们需要把这些排除掉，这也是为什么上面推导的时候$\frac{p}{q}$要保证互质
这里就可以用类似埃筛的方法，把x的因数里面算过的三角形减掉

要正着减，如果倒着，公比为$\frac{12}{8}$会先减掉公比为$\frac{9}{6}$而这里面还包含着$\frac{3}{2}$
会导致$\frac{3}{2}$被重复减掉

---

代码实现

#include 
#include 
using namespace std;
#define LL long long
#define MAXN 1000005
LL n, result;
int ok[MAXN];
int main() {
	scanf ( "%lld", &n );
	int sqt = sqrt ( n );
	for ( int i = 1;i <= sqt;i ++ ) {
		int t = i * ( 2 / ( sqrt ( 5 ) + 1 ) );
		ok[i] = i - t;
	}
	for ( LL i = 1;i <= sqt;i ++ )
		for ( LL j = i << 1;j <= sqt;j += i )
			ok[j] -= ok[i];
	for ( LL i = 1;i * i <= n;i ++ )
		result += ( n / ( i * i ) ) * ok[i];
	printf ( "%lld", result );
	return 0;
}

T2：电报

题目

给出 n 个点，每个点的出度均为 1，给出这 n 个点初始指向的点A[i] ，和改变这个点指向的目标所需要的价值 C[i]。
求让所有点强连通的最小花费。

输入格式
第一行输入一个数 n 表示点的个数。
之后的 n 行每行两个数 A[i]，C[i] 表示第 i 个点指向第 A[i] 个点，更改该点指向的点花费为 C[i]。
输出格式
共一行，为让所有点强连通的最小花费。

样例
样例输入 1
4
2 2
1 4
1 3
3 1
样例输出 1
4
样例解释 1

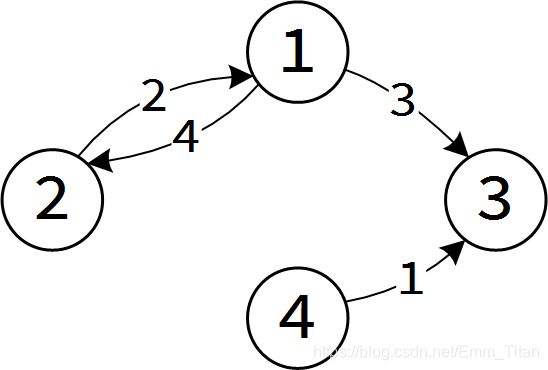
很显然，把 1–>2 的这条边改成 （花费 4）的情况下构成强连通分量花费最小。

样例输入 2
4
2 2
1 6
1 3
3 1
样例输出 2
5
样例解释 2
很显然把 1–>2 的这条边改成 1–>4 花费 2，把 3–>1 的这条边改成 3–>2 花费 3 的情况下构成强连通分量花费最小，总花费为 5。

样例输入 3
4
2 2
1 3
4 2
3 3
样例输出 3
4

样例输入 4
3
2 1
3 1
1 1
样例输出 4
0

题解

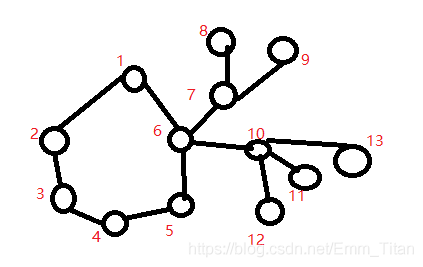
首先为了能变成强连通，树上的点彼此之间需要破掉，先不动环上的点
如图中：7，8，9和10，11，12，13就必须破掉，破成一条链
要么把7–>8破掉，要么把7–>9破掉，然后让7-8-9连成一条链

这个操作我们可以用拓扑排序找到不是环上的点，然后把这棵树破成链，如果本身是链就不进行操作

---

可以得知环彼此之间是相互独立的，就可以一次for循环先处理出所有的环
我们在上面进行树上破成链的时候，把环延伸的链或树也一起破掉
如图中：就把6–>10和6–>7都给破掉

---

接着如果变成强连通，环与环之间必须相互有路去连通，就是复活环与之外连的某一条边
意味着我们要把环破掉一条边和外界相连

那么这个时候，对于环上的最佳答案点肯定满足把它与它父亲在环上的边破掉，然后把它与自己延伸的链的点进行相连的操作最小
破环就是自己的C值，与链上的点保留一条边，就是找链上点的C的最大值

如图中：我们要把6–>1破掉，复活6–>7或者6–>10任意一条边
而且必须复活至少一条，这样才能让环与外面进行连通
但是如果图上有多个点的复活值是负数，那么肯定是都可以选的，就全都选上，可以使答案变得更小

在上面破环与链的边的时候，我们就记录最大值的C，复活的时候，肯定复活这一条边，其他边的消耗远小于这一条边破掉的消耗

---

最后我们来解释一下代码的一些地方，旁边的小姐姐问了我很久
1.为什么是建反图：
想一想，如果我们建正图，每个点都只会有一个指向点，即每个点的vector里面都只有1个点，怎么破链，复活等以上的操作呢？
换言之，每个点要知道自己有多少边连向自己，才能知道破哪些边

2.$flag||tot>1$的问题，我们要知道，
当只有环的时候，如果环是多个，也需要破掉，使所有环彼此强连通
当只有一个环的时候，如果环上有链也需要破掉，不然环上的点无法走到链上的点
（这是一条有向边，单箭头暗恋 ）
所以这里是取或，当且仅当只有一个环的时候才不会考虑复活

---

代码实现

这里定义isCircle[i]
1：表示这个点不在环上（PS：可能误导了许多亲故 ）
2：表示这个点在环上且已经经过了破树或破链处理
0：表示这个点在环上但等待被处理

#include 
#include 
#include 
#include 
#include 
using namespace std;
#define MAXN 100005
queue < int > q;
vector < int > G[MAXN], circle[MAXN];
int n, tot;
bool flag;
int a[MAXN], c[MAXN];
int d[MAXN], g[MAXN], isCircle[MAXN];
long long result;

int main() {
	scanf ( "%d", &n );
	for ( int i = 1;i <= n;i ++ ) {
		scanf ( "%d %d", &a[i], &c[i] );
		G[a[i]].push_back ( i );
		d[a[i]] ++;
	}
	for ( int i = 1;i <= n;i ++ )
		if ( ! d[i] ) {
			q.push ( i );
			isCircle[i] = 1;
			flag = 1;
		}
	while ( ! q.empty() ) {
		int t = q.front();
		q.pop();
		d[a[t]] --;
		if ( ! d[a[t]] ) {
			q.push ( a[t] );
			isCircle[a[t]] = 1;
		}
	}
	for ( int i = 1;i <= n;i ++ ) {
		if ( isCircle[i] == 1 ) {//破树为链
			int Max = 0;
			for ( int j = 0;j < G[i].size();j ++ ) {
				Max = max ( Max, c[G[i][j]] );
				result += c[G[i][j]];
			}
			result -= Max;
		}
		else {
			for ( int j = 0;j < G[i].size();j ++ )
				if ( isCircle[G[i][j]] == 1 ) {//破环与外面延伸的链
					g[i] = max ( g[i], c[G[i][j]] );//记录一条链的最大值
					result += c[G[i][j]];
				}
			if ( isCircle[i] == 0 )
				tot ++;
			int x = i;
			while ( isCircle[x] == 0 ) {//分离出环
				isCircle[x] = 2;
				circle[tot].push_back ( x );
				x = a[x];
			}
		}
	}
	if ( flag || tot > 1 ) {
		for ( int i = 1;i <= tot;i ++ ) {
			int Min = 0x3f3f3f3f;
			for ( int j = 0;j < circle[i].size();j ++ )//复活
				Min = min ( Min, c[circle[i][j]] - g[a[circle[i][j]]] );
			if ( Min >= 0 )//必须复活的一条边
				result += Min;
			else {
				for ( int j = 0;j < circle[i].size();j ++ )
					if ( c[circle[i][j]] - g[a[circle[i][j]]] < 0 )//可多复活几条边
						result += c[circle[i][j]] - g[a[circle[i][j]]];
						//破掉i与fi的环上边的时候，接的那一条边肯定是接在fi上
			}
		}
	}
	printf ( "%lld", result );
	return 0;
}