hdu 5514(容斥原理)

Description
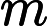
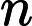
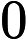
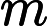
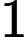
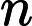
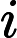
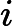
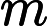
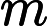
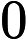
There are  stones lying on a circle, and  frogs are jumping over them. 
The stones are numbered from  to  and the frogs are numbered from  to . The -th frog can jump over exactly  stones in a single step, which means from stone  to stone  (since all stones lie on a circle). 

All frogs start their jump at stone , then each of them can jump as many steps as he wants. A frog will occupy a stone when he reach it, and he will keep jumping to occupy as much stones as possible. A stone is still considered ``occupied" after a frog jumped away. 
They would like to know which stones can be occupied by at least one of them. Since there may be too many stones, the frogs only want to know the sum of those stones' identifiers.
Input
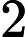
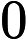
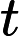
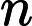
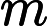
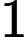
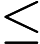
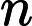
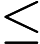
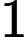
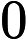
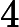
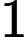
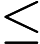
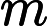
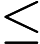
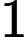
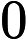
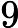
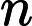
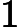
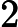
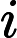
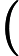
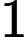
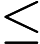
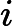
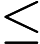
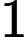
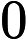
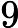
There are multiple test cases (no more than ), and the first line contains an integer , 
meaning the total number of test cases. 

For each test case, the first line contains two positive integer  and  - the number of frogs and stones respectively . 

The second line contains  integers , where  denotes step length of the -th frog .
Output
For each test case, you should print first the identifier of the test case and then the sum of all occupied stones' identifiers.
Sample Input
3
2 12
9 10
3 60
22 33 66
9 96
81 40 48 32 64 16 96 42 72
 
  
 
  
 
  
 
   
 Sample Output
 
   
 
    
Case #1: 42
Case #2: 1170
Case #3: 1872
 
    
 
     
 
    
 
   
 
  
 
  
 
  
 
  
#include
#include
#include
#include
#include
using namespace std;
#define maxn 10005
#define LL __int64
int gcd(int a,int b)
{
    return b==0?a:gcd(b,a%b);
}

int factor[maxn];
int num[maxn],vis[maxn];
int main()
{
    int T,cas = 1;
    scanf("%d",&T);
    while(T--)
    {
        int n,m,cnt = 0;
        memset(num,0,sizeof(num));
        memset(vis,0,sizeof(vis));
        scanf("%d%d",&n,&m);
        for(int i=1; i<=(int)sqrt(m); i++)
        {
            if(m%i==0)
            {
                factor[cnt++] = i;
                if(i*i!=m)
                    factor[cnt++] = m/i;
            }
        }
        sort(factor,factor+cnt);
        while(n--)
        {
            int d; scanf("%d",&d);
            int tmp = gcd(d,m);
            for(int i=0; i