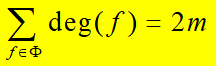电子科技大学《图论及其应用》复习总结--第六章 平面图
第六章 平面图
一、平面图概念与性质
(一)、平面图的概念
定义1 如果能把图G画在平面上,使得除顶点外,边与边之间没有交叉,称G可以嵌入平面,或称G是可平面图。可平面图G的边不交叉的一种画法,称为G的一种平面嵌入,G的平面嵌入表示的图称为平面图。
注: (1) 可平面图概念和平面图概念有时可以等同看待;
(2) 图的平面性问题主要涉及如下几个方面:
1) 平面图的性质;
2) 平面图的判定;
3) 平面嵌入方法(平面性算法) ;
4)涉及图的平面性问题的拓扑不变量。
(二)、平面图性质
定义2
(1) 一个平面图G把平面分成若干连通片,这些连通片称为G的区域,或G的一个面。G的面组成的集合用Φ表示。
(2) 面积有限的区域称为平面图G的内部面,否则称为G的外部面。
(3) 在G中,顶点和边都与某个给定区域关联的子图,称为该面的边界。某面 f 的边界中含有的边数(割边计算2次)称为该面 f 的次数, 记为deg ( f )。
1、平面图的次数公式
定理1 设G=(n, m)是平面图,则:
2、平面图的欧拉公式
定理2(欧拉公式) 设G=(n, m)是连通平面图,ф是G的面数,则:
3、欧拉公式的几个有趣推论
推论1 设G是具有ф个面k个连通分支的平面图,则:
推论2 设G是具有n个点m条边ф个面的连通平面图,如果对G的每个面f ,有:deg (f) ≥ l ≥3,则:(可平面图性质)
推论3 设G是具有n个点m条边ф个面的简单平面图,则:
推论4 设G是具有n个点m条边的连通平面图,若G的每个圈均由长度是 l 的圈围成,则:
推论5 设G是具有n个点m条边的简单平面图,则:
定理3 一个连通平面图是2连通的,当且仅当它的每个面的边界是圈。
推论6 若一个平面图是2连通的,则它的每条边恰在两个面的边界上。
(三)、图的嵌入性问题简介
1、曲面嵌入
1)、球面嵌入
定理4 G可球面嵌入当且仅当G可平面嵌入。
2)、环面嵌入
- 定向曲面嵌入
2、图的3维空间嵌入
定理5 所有图均可嵌入R3中。
(四)、凸多面体与平面图
一个多面体称为凸多面体,如果在体上任取两点,其连线均在体上。
凸多面体的一维骨架:把一个凸多面体压缩在平面上,得到一个对应的平面图,该平面图称为该凸多面体的一维骨架。**
定理6 存在且只存在5种正多面体:它们是正四、六、八、十二、二十面体。
二、特殊平面图与平面图的对偶图
(一)、特殊平面图
1、极大平面图及其性质
定义1 设G是简单可平面图,如果G是Ki (1≦i≦4),或者在G的任意非邻接顶点间添加一条边后,得到的图均是非可平面图,则称G是极大可平面图。
注:只有在单图前提下才能定义极大平面图。
引理 设G是极大平面图,则G必然连通;且若G的阶数大于等于3,则G无割边。
定理1 设G是至少有3个顶点的平面图,则G是极大平面图,当且仅当G的每个面的次数是3且为单图。(“极大平面图的三角形特征”,即每个面的边界是三角形。)
2、极大外平面图及其性质
定义3 若一个可平面图G存在一种平面嵌入,使得其所有顶点均在某个面的边界上,称该图为外可平面图。外可平面图的一种外平面嵌入,称为外平面图。
定义4 设G是一个简单外可平面图,若在G中任意不邻接顶点间添上一条边后,G成为非外可平面图,则称G是极大外可平面图。极大外可平面图的外平面嵌入,称为极大外平面图。
引理 设G是一个连通简单外可平面图,则在G中存 在度数至多是2的顶点。(证明略)
设G是一个具有n (n≥4)个点,m条边的简单连通外平面图。若G不含三角形,则m≤(3n–4)/2
定理2 设G是一个有n (n≥3)个点,且所有点均在外部面上的极大外平面图,则G有n-2个内部面。
定理3 设G是一个有n (n≥3)个点,且所有点均在外部面上的外平面图,则G是极大外平面图,当且仅当其外部面的边界是圈,内部面是三角形。
定理4 每个至少有7个顶点的外可平面图的补图不是外可平面图,且7是这个数目的最小者。
设G是一个阶数为n (n≥4)且所有点均在外部面上的极大外平面图,则G中存在两个度数均为2且不相邻的点
图G是可平面的当且仅当它不含与K5或K3,3同胚的子图
3、其他
如果在不可平面图G中任意删去一条边所得的图为可平面图,则称G为极小不可平面图。例如K5和K3,3
(二)、平面图的对偶图
1、对偶图的定义
定义4 给定平面图G,G的对偶图G*如下构造:
(1) 在G的每个面fi内取一个点vi*作为G*的一个顶点;
(2) 对G的一条边e, 若e是面 fi 与 fj 的公共边,则连接vi与vj,且连线穿过边e;若e是面 fi 中的割边,则以vi为顶点
作环,且让它与e相交。
2、对偶图的性质
(1)、G与G*的对应关系
1) G\*的顶点数等于G的面数;
2) G*的边数等于G的边数;
3) G*的面数等于G的顶点数;
4) d (v*)=deg( f )
(2)、定理5 平面图G的对偶图必然连通
注: (1) 由定理5知:(G*)*不一定等于G;
(2) G是平面图,则 ( ( G ) ∗ ) ∗ ≅ G ((G)^\ast)^\ast \cong G ((G)∗)∗≅G当且仅当G是连通的。(习题第26题)
例2 证明:
(1) B是平面图G的极小边割集,当且仅当
是G*的圈。
(2) 欧拉平面图的对偶图是偶图。
三、平面图的判定与涉及平面性不变量
定义1 在图G的边上插入一个2度顶点,使一条边分成两条边,称将图在2度顶点内扩充;去掉一个图的2度顶点,使关联它们的两条边合并成一条边,称将图G在2度顶点内收缩。
定义2 两个图G1与G2说是同胚的,如果 G 1 ≅ G 2 G_1\cong G_2 G1≅G2,或者通过反复在2度顶点内扩充和收缩后能够变成一对同构的图。
定理1 (库拉托斯基定理) 图G是可平面的,当且仅当它不含K5和K3,3同胚的子图。
定义3 给定图G, 去掉G中的环,用单边代替平行边而得到的图称为G的基础简单图。
定理2 (1) 图G是可平面的,当且仅当它的基础简单图是可平面的; (2) 图G是可平面图当且仅当G的每个块是可平面图。
定义4 设uv是简单图G的一条边。去掉该边,重合其端点,再删去由此产生的环和平行边。这一过程称为图G的初等收缩或图的边收缩运算。
定理2 (瓦格纳定理):简单图G是可平面图当且仅当它不含有可收缩到K5或K3,3的子图。
四、平面性算法
定义1 设H是G的一个子图,在E(G)-E(H)中定义一个二元关系“ ~”:
∀ e 1 , e 2 ∈ E ( G ) − E ( H ) \forall e_1,e_2\in E(G)-E(H) ∀e1,e2∈E(G)−E(H), e 1 ∼ e 2 e_1\sim e_2 e1∼e2当且仅当存在一条途径W,使得:
(1) e1与e2分别是W的始边和终边,且 (2) W的内点与H不能相交。
定义2 设B是E(G)-E(H)关于二元关系“ ~” 的等价类在G中的边导出子图,则称B是G关于子图H的一座桥。桥与H的公共顶点称为桥B在H中的附着顶点。
定义3 设H是图G的可平面子图, H ~ \tilde{H} H~是H的一种平面嵌入。若G也是可平面图,且存在G的一个平面嵌入 G ~ \tilde{G} G~ ,使得: H ~ ⊆ G ~ \tilde{H}\subseteq \tilde{G} H~⊆G~,称 H ~ \tilde{H} H~是G容许的
定义4 设B是G中子图H的任意一座桥,若B对H的所有附着顶点都位于 的某个面 f 的边界上,则称B在面 f 内可画入,否则,称B在面 f 内不可画入。
算法:
(1) 取G的一个圈H1,求出H1的一个平面嵌入 H 1 ~ \tilde{H1} H1~ 。置i=1;
(2) 若E(G)-E(Hi)=Φ,则停止;否则,确定G中Hi的所有桥,并对每座桥B,求出 F ( B , H i ~ ) F(B,\tilde{H_i}) F(B,Hi~) ;
(3) 若存在桥B,使得: F ( B , H i ~ ) = ϕ F(B,\tilde{H_i})=\phi F(B,Hi~)=ϕ ,则停止 (G不可平面) ;否则,在Hi的所有桥中确定一个使得 ∣ F ( B , H i ~ ) ∣ |F(B,\tilde{H_i})| ∣F(B,Hi~)∣最小的B,并取 f ∈ F ( B , H i ~ ) f\in F(B,\tilde{H_i}) f∈F(B,Hi~)
(4) 在桥B中取一条连接Hi中两个附着顶点的路Pi, P i ⊆ B i P_i\subseteq B_i Pi⊆Bi 。 置Hi+1=Hi∪Pi,把Pi画在 H i ~ \tilde{H_i} Hi~的面 f 内,得到 H i + 1 ~ \tilde{H_{i+1}} Hi+1~
(5) 置i=i+1转(2)。
总结:重要的性质定理
1、平面图的性质(包括次数公式,欧拉公式,一些推论)
-
次数公式:设G=(n, m)是平面图,则: ∑ f ∈ ϕ d e f ( f ) = 2 m \sum_{f\in \phi} def(f)=2m ∑f∈ϕdef(f)=2m
-
欧拉公式:设G=(n, m)是连通平面图,ф是G的面数,则: n − m + ϕ = 2 n-m+\phi =2 n−m+ϕ=2
-
推论1 设G是具有ф个面k个连通分支的平面图,则: n − m + ϕ = k + 1 n-m+\phi =k+1 n−m+ϕ=k+1
-
推论2 设G是具有n个点m条边ф个面的连通平面图,如果对G的每个面f ,有:deg (f) ≥ l ≥3,则: m ≤ l l − 2 ( n − 2 ) m\leq \frac{l}{l-2}(n-2) m≤l−2l(n−2)
-
推论3 设G是具有n个点m条边ф个面的简单平面图,则: m ≤ 3 n − 6 m\leq3n-6 m≤3n−6
-
推论4 设G是具有n个点m条边的连通平面图,若G的每个圈均由长度是 l 的圈围成,则: m ( l − 2 ) = l ( n − 2 ) m(l-2)=l(n-2) m(l−2)=l(n−2)
-
推论5 设G是具有n个点m条边的简单平面图,则: δ ≤ 5 \delta \leq5 δ≤5
-
K5和K3,3是非可平面图
-
彼得森图是非可平面图
2、嵌入性和特殊平面图
- G可球面嵌入当且仅当G可平面嵌入。
- 存在且只存在5种正多面体:它们是正四、六、八、十二、二十面体
- 设G是至少有3个顶点的平面图,则G是极大平面图,当且仅当G的每个面的次数是3且为单图。(“极大平面图的三角形特征”,即每个面的边界是三角形。)
2、平面图的判定
(1)对于简单图G=(n,m),如果m>3n-6,则G是非可平面的;
(2)对于简单连通图G=(n,m),如果每个面次数至少为 l ≥ 3 l\geq3 l≥3,且 m > l ( n − 2 ) l − 2 m>\frac{l(n-2)}{l-2} m>l−2l(n−2),则G是非可平面的;
(3) (库拉托斯基定理) 图G是可平面的,当且仅当它不含K5和K3,3同胚的子图。
(4)(瓦格纳定理):简单图G是可平面图当且仅当它不含有可收缩到K5或K3,3的子图。
3、平面性算法
找一个圈—>找出所有的桥—>依次选取桥可嵌入最小的平面数进行嵌入—>画出平面图(否则不存在)
总结:一些结论
-
无环图是2连通的平面图,一定不包含割点,同时不包含割边,一定不包含只属于一个面的边,边界均为圈
-
若(n,m)图是极大外平面图且n大于等于3,则m=2n-3
-
阶数至少为3的极大外平面图一定是H图
-
G是一个简单图,若顶点数n≥11,则G与G的补图中,至少有一个是不可平面图
-
设G是一个具有n (n≥4)个点,m条边的简单连通外平面图。若G不含三角形,则m≤(3n–4)/2