Kalman滤波学习笔记二《数学基础：向量与矩阵》

学习笔记参考：《Kalman滤波基础及MATLAB仿真》北京航空航天大学出版社——王可东编著
注：本篇笔记根据博主个人数学的掌握情况整理

一、向量
1、内积：同维数的两个向量可以求内积，结果为对应元素的乘积之和，为一标量。$${\mathbf{x}}^T\mathbf{y}={\mathbf{y}}^T\mathbf{x}=\sum _{i=1}^n{x}_i{y}_i$$ 如果${\mathbf{x}}^T\mathbf{y}=0$，则 $x$ 与 $y$ 正交；$x$ 的长度：$|\mathbf{x}|=\sqrt{{\mathbf{x}}^T\mathbf{x}}$。
2、外积：同维数的两个向量可以求外积，结果为一方阵。
$$\mathbf{x}{\mathbf{y}}^T=\left(\begin{array}{cccc}{x}_1{y}_1& x_1{y}_2& \cdots & x_1{y}_n\\ x_2{y}_1& x_2{y}_2& \cdots & x_2{y}_n\\ ⋮& ⋮& \ddots & ⋮\\ x_n{y}_1& x_n{y}_2& \cdots & x_n{y}_n\end{array}\right)$$ $\mathbf{x}$ 的扩散矩阵为：
$$\mathbf{x}{\mathbf{x}}^T=\left(\begin{array}{cccc}{x}_1^2& x_1{x}_2& \cdots & x_1{x}_n\\ x_2{x}_1& x_2^2& \cdots & x_2{x}_n\\ ⋮& ⋮& \ddots & ⋮\\ x_n{x}_1& x_n{x}_2& \cdots & x_n^2\end{array}\right)$$ 3、导数：向量的导数为其每个元素求导。
4、积分：向量的积分为其每个元素积分。

二、矩阵
1、导数和积分：矩阵的导数和积分为对其每个元素求导数和积分。
2、单位矩阵：
$$\mathbf{I}=\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right)=[{\delta }_{ij}]$$ 其中，${\delta }_{ij}$ 为Kronecker $\delta$ 函数，定义为：
$${\delta }_{ij}=\{\begin{array}{ll}1,& i=j\\ 0,& i\ne j\end{array}$$3、迹：方阵主对角线上元素的代数和称为该方阵的迹：$$tr(\mathbf{A})=\sum _{i=1}^n{a}_{ii}$$4、伪逆：对 ${\mathbf{A}}_{m\times n}$，m>n，且 $({\mathbf{A}}^T\mathbf{A})$ 非奇异，则其伪逆定义为：
$${\mathbf{A}}^{\#}=({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T$$ 若 m $${\mathbf{A}}^{\#}={\mathbf{A}}^T(\mathbf{A}{\mathbf{A}}^T{)}^{-1}$$ 伪逆的运算性质有：
$$\{\begin{array}{c}\mathbf{A}{\mathbf{A}}^{\#}\mathbf{A}=\mathbf{A}\\ {\mathbf{A}}^{\#}\mathbf{A}{\mathbf{A}}^{\#}={\mathbf{A}}^{\#}\\ ({\mathbf{A}}^{\#}\mathbf{A}{)}^T={\mathbf{A}}^{\#}\mathbf{A}\\ (\mathbf{A}{\mathbf{A}}^{\#}{)}^T=\mathbf{A}{\mathbf{A}}^{\#}\end{array}$$ 5、方阵函数：$\lambda$ 为方阵 $\mathbf{A}$ 的特征值，特征方程为：
$$f(\lambda )=|\lambda \mathbf{I}-\mathbf{A}|={\lambda }^n+a_1{\lambda }^{n-1}+a_2{\lambda }^{n-2}+\cdots +a_{n-1}{\lambda }^1+a_n=0$$ 由Cayley公式知，将方阵 $\mathbf{A}$ 代入特征方程有：$f(\mathbf{A})=0$
对方阵 $\mathbf{A}$ 定义其对应的指数矩阵为：
$$e^{\mathbf{A}}=\mathbf{I}+\mathbf{A}+\frac{1}{2!}{\mathbf{A}}^2+\cdots$$ 其中，${\mathbf{A}}^2=\mathbf{A}\mathbf{A},{\mathbf{A}}^3=\mathbf{A}\mathbf{A}\mathbf{A},{\mathbf{A}}^{k+1}=({\mathbf{A}}^k)\mathbf{A}$ 。指数矩阵性质有：
① 若 $\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}$ ，则 $e^{\mathbf{A}+\mathbf{B}}=e^{\mathbf{A}}{e}^{\mathbf{B}}$；
② 若 $|\mathbf{T}|\ne 0$ ，则$e^{\mathbf{T}\mathbf{F}{\mathbf{T}}^{-1}}=\mathbf{T}{e}^{\mathbf{F}}{\mathbf{T}}^{-1}$；
③ $|e^{\mathbf{F}}|=e^{tr(\mathbf{F})}$ 。

三、向量—矩阵运算
1、二次型：设 ${\mathbf{A}}_{n\times n}$ 为一对称矩阵，$\mathbf{x}$ 为一 $n$ 维列向量，那么关于对称矩阵 $\mathbf{A}$ 的二次型定义为：$$J={\mathbf{x}}^T\mathbf{A}\mathbf{x}$$若 $\mathbf{A}$ 的特征值为 $\{{\lambda }_i\}(i=1,2,\cdots ,n)$，那么，存在正交矩阵 $\mathbf{Q}$，使得：$$J={\mathbf{x}}^T\mathbf{A}\mathbf{x}={{\mathbf{x}}^{\prime }}^T{\mathbf{A}}^{\prime }{\mathbf{x}}^{\prime }=\sum _{i=1}^n{\lambda }_i{x_i^{\prime }}^2$$其中，$x^{\prime }={\mathbf{Q}}^T\mathbf{x}$，${\mathbf{A}}^{\prime }={\mathbf{Q}}^T\mathbf{A}\mathbf{Q}=diag({\lambda }_i)$，$diag(\cdot )$ 表示对角线上的元素为相应值，其它非对角线元素均为 $0$。
2、定：对于对称方阵 $\mathbf{A}$，按照其二次型的结果，定义如下四种定：
① 正定：$J={\mathbf{x}}^T\mathbf{A}\mathbf{x}>0$；
② 负定：$J={\mathbf{x}}^T\mathbf{A}\mathbf{x}<0$；
③ 半正定：$J={\mathbf{x}}^T\mathbf{A}\mathbf{x}\ge 0$；
③ 半负定：$J={\mathbf{x}}^T\mathbf{A}\mathbf{x}\le 0$；
对于物理可实现系统，其对应的系数矩阵都是正定的，与可逆也是等价的。
3、范数：
向量 $\mathbf{x}$ 的范数 $||\mathbf{x}||$ 需满足如下三个条件：
① $||k\mathbf{x}||=|k|||\mathbf{x}||$，其中 $k$ 为标量；
② $||\mathbf{x}+\mathbf{y}||\le ||\mathbf{x}||+||\mathbf{y}||$；
③ 若 $||\mathbf{x}||=0$，则 $\mathbf{x}=0$ 。
显然，满足上述条件的范数有很多种，其中最常见的有：
① $Euclid$ 范数 (2 范数)：$$||\mathbf{x}|{|}_2=\sqrt{{\mathbf{x}}^T\mathbf{x}}$$② $Manhattan$ 范数 (1 范数)：$$||\mathbf{x}|{|}_1=\sum _{i=1}^n|x_i|$$③ 无穷范数：$$||\mathbf{x}|{|}_{\infty }=max(|x_1|,|x_2|,\cdots ,|x_n|)$$④ $p$ 范数：设 $p$ 为一不小于1的实数，$p$ 范数定义为：$$||\mathbf{x}|{|}_p=(\sum _{i=1}^n|x_i{|}^p{)}^{\frac{1}{p}}$$类似地，也可以定义矩阵 ${\mathbf{A}}_{m\times n}$ 的范数如下：
① 1 范数：$${||\mathbf{A}||}_1=\underset{1⩽j⩽n}{\max }\sum _{i=1}^m|a_{ij}|$$② 无穷范数：$${||\mathbf{A}||}_{\infty }=\underset{1⩽i⩽m}{\max }\sum _{j=1}^n|a_{ij}|$$③ 2 范数：$${||\mathbf{A}||}_2=\sqrt{{\lambda }_{max}({\mathbf{A}}^{\ast }\mathbf{A}})$$其中，${\mathbf{A}}^{\ast }$ 为 $\mathbf{A}$ 的复共轭转置矩阵，${\lambda }_{max}$ 为 ${\mathbf{A}}^{\ast }\mathbf{A}$ 的最大特征值。
④ $Frobenius$ 范数：$${||\mathbf{A}||}_F=(\sum _{i=1}^m\sum _{j=1}^n|a_{ij}{|}^2{)}^{\frac{1}{2}}$$ 4、梯度运算：
① 标量函数对一向量求梯度：
标量对一向量求梯度运算为该标量对向量的每个元素求梯度，构成一向量，因而，梯度运算得到的向量与求梯度运算的向量同维数，即：$$\frac{\partial z}{\partial \mathbf{x}}=\mathbf{a}$$其中，$a_i=\frac{\partial z}{\partial x_i}$ 。
② 内积：
内积也为标量，其梯度运算结果为：$$\frac{\partial }{\partial \mathbf{x}}({\mathbf{y}}^T\mathbf{x})=\mathbf{y}$$ $$\frac{\partial }{\partial \mathbf{x}}({\mathbf{x}}^T\mathbf{y})=\mathbf{y}$$③ 标量函数对一向量的二阶梯度：
标量对一向量求二阶梯度，结果为一方阵，即：$$\frac{{\partial }^{2}z}{\partial {\mathbf{x}}^2}=\mathbf{A}$$其中，$a_{ij}=\frac{{\partial }^{2}z}{\partial x_i\partial x_j}$，$|\mathbf{A}|$ 为 $z$ 的 $Hessian$ 矩阵行列式。
④ 向量对向量求梯度：
一向量对另一向量求梯度，为向量的每个元素对另一向量的每个元素求梯度，结果为一矩阵，即：$$\frac{\partial {\mathbf{z}}^T}{\partial \mathbf{x}}=\mathbf{A}$$其中，$a_{ij}=\frac{\partial z_j}{\partial x_i}$ 。若 $\mathbf{z}$ 与 $\mathbf{x}$ 同维，则 $|\mathbf{A}|$ 为 $\mathbf{z}$ 的 $Jacobian$ 矩阵行列式。
⑤ 标量对矩阵求梯度：
标量对矩阵求梯度，为标量对矩阵的每个元素求梯度，结果为同维度矩阵，即：$$\frac{\partial z}{\partial \mathbf{A}}=\mathbf{B}$$其中，$b_{ij}=\frac{\partial z}{\partial a_{ij}}$，$\mathbf{B}$ 矩阵又称为 $Hessian$ 矩阵。
对方阵 $\mathbf{A}$、$\mathbf{B}$ 和 $\mathbf{C}$，有如下式子成立：$$\frac{\partial }{\partial \mathbf{A}}tr(\mathbf{A})=\mathbf{I}$$ $$\frac{\partial }{\partial \mathbf{A}}tr(\mathbf{B}\mathbf{A}\mathbf{C})={\mathbf{B}}^T{\mathbf{C}}^T$$ $$\frac{\partial }{\partial \mathbf{A}}tr(\mathbf{A}\mathbf{B}{\mathbf{A}}^T)=\mathbf{A}({\mathbf{B}}^T+\mathbf{B})$$ $$\frac{\partial }{\partial \mathbf{A}}tr(e^{\mathbf{A}})=e^{{\mathbf{A}}^T}$$ $$\frac{\partial }{\partial \mathbf{A}}|\mathbf{B}\mathbf{A}\mathbf{C}|=|\mathbf{B}\mathbf{A}\mathbf{C}|({\mathbf{A}}^{-1}{)}^T$$ ⑥ 二次型求梯度：$$\frac{\partial {\mathbf{x}}^T\mathbf{A}\mathbf{x}}{\partial \mathbf{x}}=(\mathbf{A}+{\mathbf{A}}^T)\mathbf{x}$$  
四、最小二乘算法
1、例一：设一向量 $\mathbf{x}$，其对应的测量向量为 $\mathbf{z}$，且有 $\mathbf{z}=\mathbf{H}\mathbf{x}+\mathbf{v}$，其中 $\mathbf{H}$ 为量测矩阵，$\mathbf{v}$ 为量测噪声。最优准则设置为：测量值与其估计值的偏差平方和最小，试求基于 $\mathbf{z}$ 关于 $\mathbf{x}$ 的最优估计。
解：设 $\mathbf{x}$ 的估计值为 $\hat{\mathbf{x}}$，其中量测噪声是无法估计的，那么测量值的估计为 $\hat{\mathbf{z}}=\mathbf{H}\hat{\mathbf{x}}$。按照估计准则有：$$J=(\mathbf{z}-\hat{\mathbf{z}}{)}^T(\mathbf{z}-\hat{\mathbf{z}})=(\mathbf{z}-\mathbf{H}\hat{\mathbf{x}}{)}^T(\mathbf{z}-\mathbf{H}\hat{\mathbf{x}})$$ $J$ 是关于 $\hat{\mathbf{x}}$ 的函数，且为平方和的形式，因此，当：$$\frac{\partial J}{\partial \hat{\mathbf{x}}}=0$$ 时，$J$ 取极小值，有：$$\frac{\partial J}{\partial \hat{\mathbf{x}}}={\left[\frac{\partial (\mathbf{z}-\mathbf{H}\hat{\mathbf{x}})}{\partial \hat{\mathbf{x}}}\right]}^T\left[\frac{\partial \left[(\mathbf{z}-\mathbf{H}\hat{\mathbf{x}}{)}^T\mathbf{I}(\mathbf{z}-\mathbf{H}\hat{\mathbf{x}})\right]}{\partial (\mathbf{z}-\mathbf{H}\hat{\mathbf{x}})}\right]=-{\mathbf{H}}^T(\mathbf{I}+{\mathbf{I}}^T)(\mathbf{z}-\mathbf{H}\hat{\mathbf{x}})$$ $$=-2{\mathbf{H}}^T\mathbf{z}+2{\mathbf{H}}^T\mathbf{H}\hat{\mathbf{x}}=0$$ 当 ${\mathbf{H}}^T\mathbf{H}$ 可逆时，有：$$\hat{\mathbf{x}}=({\mathbf{H}}^T\mathbf{H}{)}^{-1}{\mathbf{H}}^T\mathbf{z}$$ 上式就是基于 $\mathbf{z}$ 测量值对 $\mathbf{x}$ 在最小二乘意义上的最优估计结果。
注：上述求导过程运用到矩阵向量的链式求导法则。
2、例二：设一辆汽车在一条公路上匀速直线行驶，速度为 $30m/s$。车上安装了BDS接收机，其测速误差是均值为 $0$、标准差为 $0.1m/s$ 的高斯噪声；同时，车载测速仪的测速误差是均值为 $0$、标准差为 $0.5m/s$ 的高斯噪声。试利用最小二乘算法估计该车辆 $100s$ 之内的速度，并与Kalman滤波学习笔记一第12条的结果进行对比。
解：k时刻的测量量为：$${\mathbf{z}}_k=\left[\begin{array}{c}{z}_{1,k}\\ z_{2,k}\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right]x_k+\left[\begin{array}{c}{v}_{1,k}\\ v_{2,k}\end{array}\right]={\mathbf{H}}_k{x}_k+{\mathbf{v}}_k$$ 而最小二乘算法是批处理算法，即累积从初始时刻到k时刻的所有测量值，对k时刻的状态进行估计，因此，k时刻利用的测量量为：$${\bar{\mathbf{z}}}_k=\left[\begin{array}{c}{\mathbf{z}}_1\\ {\mathbf{z}}_2\\ ⋮\\ {\mathbf{z}}_k\end{array}\right]=\left[\begin{array}{c}{\mathbf{H}}_1\\ {\mathbf{H}}_2\\ ⋮\\ {\mathbf{H}}_k\end{array}\right]x_k+\left[\begin{array}{c}{\mathbf{v}}_1\\ {\mathbf{v}}_2\\ ⋮\\ {\mathbf{v}}_k\end{array}\right]={\overline{\mathbf{H}}}_k{x}_k+{\bar{\mathbf{v}}}_k$$ 则 ${\mathbf{x}}_k$ 在最小二乘意义上的最优估计结果为：$${\hat{\mathbf{x}}}_k=({\overline{\mathbf{H}}}_k^T{\overline{\mathbf{H}}}_k{)}^{-1}{\overline{\mathbf{H}}}_k^T{\bar{\mathbf{z}}}_k=\frac{1}{2k}\sum _{i=1}^k(z_{1,i}+z_{2,i})$$

MATLAB代码如下：

clear all; close all;

N = 100;
x = 50 * ones(N,1);  %被估计对象
sigma1 = 0.5; sigma2 = 0.1;
v1 = sigma1 * randn(N,1);
v2 = sigma2 * randn(N,1);
z1 = x + v1;
z2 = x + v2;

w1 = sigma1^2/(sigma1^2 + sigma2^2);
w2 = sigma2^2/(sigma1^2 + sigma2^2);
x_est = w1 * z2 + w2 * z1;

x_est_ls_1 = [];
x_est_ls_2 = [];
sum_1 = 0;
sum_2 = 0;

for i = 1:N
    sum_1 = sum_1 + z1(i);
    sum_2 = sum_2 + z2(i);
    est_1 = sum_1/i;
    est_2 = (sum_1 + sum_2)/(2*i);
    x_est_ls_1 = [x_est_ls_1;est_1];
    x_est_ls_2 = [x_est_ls_2;est_2];
end
x_est_err = x_est-x;
x_est_ls_1_err = x_est_ls_1 - x;
x_est_ls_2_err = x_est_ls_2 - x;

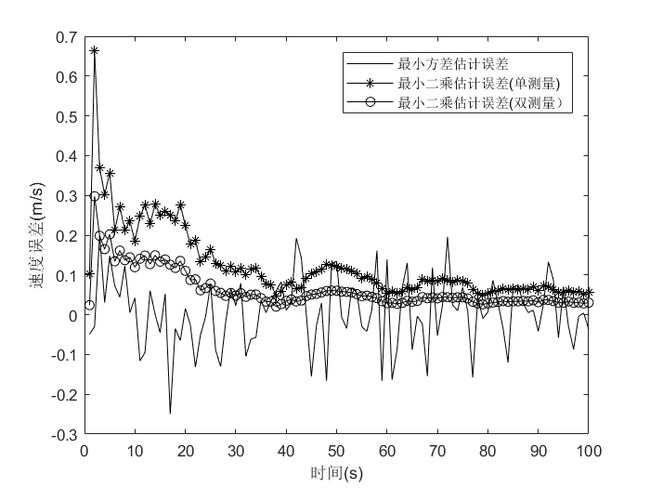
plot(1:N,x_est_err,'k',1:N,x_est_ls_1_err,'k*-',1:N,x_est_ls_2_err,'ko-')
legend('最小方差估计误差','最小二乘估计误差(单测量)','最小二乘估计误差(双测量）');
xlabel('时间(s)');ylabel('速度误差(m/s)')

两个结论：
① 为了提高估计精度，应尽可能地利用从初始时刻到当前时刻的所有测量值，实现对当前时刻的状态估计；
② 基于多个传感器的测量结果进行状态估计有利于提高估计精度。

 
 
课后习题
1、设矩阵 $\mathbf{A}=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$：
① 试求矩阵 $\mathbf{A}$ 的特征值 ${\lambda }_1$ 和 ${\lambda }_2$ 以及 ${\mathbf{A}}^3$ 和 ${\mathbf{A}}^5$；
② 若 $e^{\mathbf{A}t}=a\mathbf{I}+b\mathbf{A}$，试证明 $a=\frac{{\lambda }_1{e}^{{\lambda }_{2}t}-{\lambda }_2{e}^{{\lambda }_{1}t}}{{\lambda }_1-{\lambda }_2}$，$b=\frac{e^{{\lambda }_{1}t}-e^{{\lambda }_{2}t}}{{\lambda }_1-{\lambda }_2}$。
2、试证明：
① ${\dot{\mathbf{P}}}^{-1}=-{\mathbf{P}}^{-1}\dot{\mathbf{P}}{\mathbf{P}}^{-1}$；
② 若 $\mathbf{R}(t)$ 为时变正交矩阵，且满足 $\dot{\mathbf{R}}(t){\mathbf{R}}^T(t)=\mathbf{S}(t)$，求证 $\mathbf{S}(t)$ 为反对称阵。

参考答案如下：