数据挖掘-Task3 特征工程
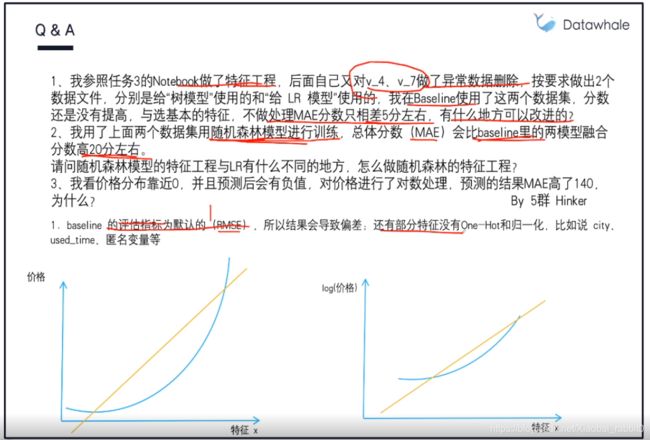
数据挖掘-Task3 特征工程
- 特征工程目标
- 1 内容介绍
- 1.1 数据理解
- 1.2 数据清洗
- 1.3 特征构造
- 1.4 特征选择
- 1.5 类别不平衡
- 2 代码示例
- 2.1 数据理解
- 2.1.1 加载库
- 2.1.2 加载数据
- 2.1.3 预览数据
- 2.2 数据清洗
- 2.3 删除无用特征
- 2.4 缺失值填充
- 2.5 特征构造
- 2.6 数据分桶
- 2.7 特征筛选
- 2.7.1 过滤式
- 2.7.2 嵌入式
- 2.8 经验总结
- 2.9 Q&A 来自Datawhale答疑
特征工程目标
特征工程(Feature Engineering):将数据转换为能更好地表示潜在问题的特征,从而提高机器学习性能。
常见的特征工程包括:
- 异常处理:
- 通过箱线图(或3-Sigma)分析删除异常值;
- BOX-COX转换(处理有偏分布);
- 长尾截断;
- 特征归一化/标准化:
- 标准化(转换为标准正态分布);
- 归一化(转换到[0,1]区间);
- 数据分桶:
- 等频分桶;
- 等距分桶;
- Best-KS分桶(类似利用基尼指数进行二分类);
- 卡方分桶;
- 缺失值处理:
- 不处理(针对类似XGBoost等树模型);
- 删除(缺失数据太多);
- 插值补全,包括均值、中位数、众数、建模预测、多重插补、压缩感知补全、矩阵补全等;
- 分箱,缺失值一个箱;
- 特征构造:
- 构造统计量特征,报告计数、求和、比例、标准差等;
- 时间特征,包括相对时间和绝对时间,节假日,双休日等;
- 地理信息,包括分箱,分布编码等方法;
- 非线性变换,包括log、平方、根号等;
- 特征组合,特征交叉;
- 仁者见仁,智者见智;
- 特征筛选
- 过滤式(filter):先对数据进行特征选择,然后再训练学习器,常见的方法有Relief、方差选择法、相关系数法、卡方检验法、互信息法;
- 包裹式(wrapper):直接把最终要使用的学习器的性能作为特征子集的评价准则,常见方法有LVM(Las Vegas Wrapper);
- 嵌入式(embedding):结合过滤式和包裹式,学习器训练过程中自动进行了特征选择,常见的有lasso回归;
- 降维
- PCA、LDA、ICA;
- 特征选择也是一种降维
1 内容介绍
- 数据理解;
- 数据清洗;
- 特征构造;
- 特征选择;
- 类别不平衡。
1.1 数据理解
见上一篇,数据的探索性分析(EDA)
1.2 数据清洗
目的:提高数据质量,降低算法用错误数据建模的风险
- 特征变换:模型无法处理或不适合处理
a) 定性变量编码:Label Encoder、Onehot Encoder、Distribution Encoder;
b) 标准化和归一化:z分数标准化(标准正太分布)、min-max归一化。 - 缺失值处理:增加不确定性,可能会导致不可靠输出
a) 不处理:少量样本缺失;
b) 删除:大量样本缺失;
c) 补全:(同类)均值/中位数/众数补全、高维映射(One-hot)、模型预测、最邻近补全、矩阵补全(R-SVD)。 - 异常值处理:减少脏数据
a) 简单统计:如describe()的统计描述、散点图等;
b) 3δ法则(正态分布)、箱线图删除、截断;
c) 利用模型进行离群点检测:聚类、K近邻、One Class SVM、Lsolation Forest; - 其他:删除无效列、更改dtypes、删除列中的字符串、将时间戳从字符串转换为日期时间格式等。
1.3 特征构造
目的:增强数据表达,添加先验知识
- 统计量特征
a) 计数、求和、比例、标准差; - 时间特征
a) 绝对时间、相对时间、节假日、双休日; - 地理信息
a) 分桶 - 非线性变换
a) 取log、平方、根号; - 数据分桶
a) 等频/等距分桶、Best-KS分桶、卡方分桶; - 特征组合/特征交叉
1.4 特征选择
目的:平衡预测能力和计算复杂度,降低噪声,增强模型预测性能
- 过滤式(Filter):先用特征选择方法对初始特征进行过滤,然后再训练机器学习,特征选择过程与后续学习器无关
a) Relief、方差选择、相关系数、卡方检验、互信息法; - 包裹式(Wrapper):直接把最终将要使用的学习器的性能作为衡量特征子集的评价准则,其目的在于为给定学习器选择最有利于其性能的特征子集
a) Las Vegas Wrapper(LVM) - 嵌入式(Embedding):结合过滤式和包裹式方法,将特征选择与学习器训练过程融为一体,两者在同一优化过程中完成 ,即学习器训练过程中自动进行了特征选择
a) LR+L1或决策树
1.5 类别不平衡
目的:解决少类别信息太少,导致学习器无法学会如何判别少数类
- 扩充数据集
- 尝试其他评价指标:AUC等
- 调整θ值
- 重采样、过采样/欠采样
- 合成样本:SMOTE
- 选择其他模型:决策树等
- 加权少类别的样本错分代价
- 创新:
a) 将大类分解成多个小类
b) 将小类视为异常点,并用异常检测建模
2 代码示例
2.1 数据理解
数据的理解在上一篇文章中已经对获取的数据,进行了EDA分析,接下来是数据清洗和转换在数据挖掘中也非常重要,毕竟数据探索我们发现了问题之后,下一步就是要解决问题,通过数据清洗和转换,可以让数据变得更加整洁和干净,才能进一步帮助我们做特征工程,也有利于模型更好的完成任务。
在上一篇文章数据的探索性(EDA)分析中, 发现数据存在如下问题:
- 有缺失值,尤其是类别的那些特征(bodyType, gearbox, fullType, notRepaired)
- 类别倾斜严重的特征(seller, offtype), 考虑删除
- 类别型数据需要编码
- 数值型数据或许可以尝试归一化和标准化的操作
- 预测值需要对数转换
- power高度偏斜,这个处理异常之后对数转换试试
- 隐匿特征的相关性
- 存在高势集model, 及类别特征取值非常多, 可以考虑使用聚类的方式,然后在独热编码
============================================================== - v_13与price的相关性很差,考虑删除
- v_1与v_6相关性很强,结合它们与prince的相关性,删v_1留v_6
- v_2与v-0相关性很强,结合它们与prince的相关性,删v_2留v-0
- ============================================================
- 使用:data[‘creatDate’] - data[‘regDate’],构建汽车使用时间特征
- 使用:data[‘city’] = data[‘regionCode’].apply(lambda x : str(x)[:-3]),构建城市特征
2.1.1 加载库
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from operator import itemgetter
%matplotlib inline
2.1.2 加载数据
path = './datalab/'
train_data = pd.read_csv(path+'used_car_train_20200313.csv',sep=' ')
test_data = pd.read_csv(path+'used_car_testA_20200313.csv',sep=' ')
print(train_data.shape)
print(test_data.shape)
2.1.3 预览数据
train_data.iloc[:,:10].head().append(train_data.iloc[:,:10].tail())
train_data.iloc[:,10:20].head().append(train_data.iloc[:,10:20].tail())
train_data.iloc[:,20:].head().append(train_data.iloc[:,20:].tail())
train_data.columns
test_data.columns
重点是在整理数据清洗和转换的技巧,首先是处理异常数据,通过箱线图捕获异常点,然后截尾处理, 然后是整理一些处理缺失的技巧, 然后是数据分桶和数据转换的一些技巧。
2.2 数据清洗
大纲:
- 异常值处理(箱线图分析删除,截尾,box-cox转换技术)
- 缺失值处理(不处理, 删除,插值补全, 分箱)
- 数据分桶(等频, 等距, Best-KS分桶,卡方分桶)
- 数据转换(归一化标准化, 对数变换,转换数据类型,编码等)
- 知识总结
方法一:
================================================================
数据清洗的时候,我这里先把数据训练集和测试集放在一块进行处理,因为我后面的操作不做删除样本的处理, 如果后面有删除样本的处理,可别这么做。 数据合并处理也是一个trick, 一般是在特征构造的时候合并起来,而我发现这个问题中,数据清洗里面训练集和测试集的操作也基本一致,所以在这里先合起来, 然后分成数值型、类别型还有时间型数据,然后分别清洗。
1、先合并、分型
"""把train_data的price先保存好"""
train_target = train_data['price']
del train_data['price']
"""数据合并"""
data = pd.concat([train_data, test_data], axis=0)
data.set_index('SaleID', inplace=True)
"""把数据分成数值型和类别型还有时间型,然后分开处理"""
"""人为设定"""
numeric_features = ['power', 'kilometer']
numeric_features.extend(['v_'+str(i) for i in range(15)])
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox',
'notRepairedDamage','regionCode', 'seller', 'offerType']
time_features = ['regDate', 'creatDate']
num_data = data[numeric_features]
cat_data = data[categorical_features]
time_data = data[time_features]
trick1: 就是如果发现处理数据集的时候,需要训练集和测试集进行同样的处理,不放将它们合并到一块处理。
trick2: 如果发现特征字段中有数值型,类别型,时间型的数据等,也不妨试试将它们分开,因为数值型,类别型,时间型数据不管是在数据清洗还是后面的特征工程上, 都是会有不同的处理方式, 所以这里将训练集合测试集合并起来之后,根据特征类型把数据分开, 等做完特征工程之后再进行统一的整合(set_index把它们的索引弄成一样的,整合的时候就非常简单了)。
2、异常值处理
常用的异常值处理操作包括箱线图分析删除异常值, BOX-COX转换(处理有偏分布), 长尾截断的方式, 当然这些操作一般都是处理数值型的数据。
关于box-cox转换,一般是用于连续的变量不满足正态的时候,在做线性回归的过程中,一般线性模型假定Y=Xβ+ε, 其中ε满足正态分布,但是利用实际数据建立回归模型时,个别变量的系数通不过。例如往往不可观测的误差 ε 可能是和预测变量相关的,不服从正态分布,于是给线性回归的最小二乘估计系数的结果带来误差,为了使模型满足线性性、独立性、方差齐性以及正态性,需改变数据形式,故应用box-cox转换。具体详情这里不做过多介绍,当然还有很多转换非正态数据分布的方式:
箱线图分析具体实现
from scipy.stats import boxcox
boxcox_transformed_data = boxcox(original_data)
当然,也给出一个使用案例:使用scipy.stats.boxcox完成BoxCox变换
好了,BOX-COX就介绍这些吧, 因为这里处理数据先不涉及这个变换,我们回到这个比赛中来,通过这次的数据介绍一下箱线图筛选异常并进行截尾:
从上面的探索中发现,某些数值型字段有异常点,可以看一下power这个字段:
# power属性是有异常点的
num_data.boxplot(['power'])

所以,我们下面用箱线图去捕获异常,然后进行截尾, 这里不想用删除,一个原因是我已经合并了训练集和测试集,如果删除的话肯定会删除测试集的数据,这个是不行的, 另一个原因就是删除有时候会改变数据的分布等,所以这里考虑使用截尾的方式:
"""这里包装了一个异常值处理的代码,可以随便调用"""
def outliers_proc(data, col_name, scale=3):
"""
用于截尾异常值, 默认用box_plot(scale=3)进行清洗
param:
data: 接收pandas数据格式
col_name: pandas列名
scale: 尺度
"""
data_col = data[col_name]
Q1 = data_col.quantile(0.25) # 0.25分位数
Q3 = data_col.quantile(0.75) # 0,75分位数
IQR = Q3 - Q1
data_col[data_col < Q1 - (scale * IQR)] = Q1 - (scale * IQR)
data_col[data_col > Q3 + (scale * IQR)] = Q3 + (scale * IQR)
return data[col_name]
num_data['power'] = outliers_proc(num_data, 'power')

是不是比上面的效果好多了?当然,如果想删除这些异常点,这里是来自Datawhale团队的分享代码,后面会给出链接,也是一个模板:
================================================================
方法二:
================================================================
异常值处理(箱线图分析删除)
# 这里我包装了一个异常值处理的代码,可以随便调用。
def outliers_proc(data, col_name, scale=3):
"""
用于清洗异常值,默认用 box_plot(scale=3)进行清洗
:param data: 接收 pandas 数据格式
:param col_name: pandas 列名
:param scale: 尺度
:return:
"""
def box_plot_outliers(data_ser, box_scale):
"""
利用箱线图去除异常值
:param data_ser: 接收 pandas.Series 数据格式
:param box_scale: 箱线图尺度,
:return:
"""
iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
val_low = data_ser.quantile(0.25) - iqr
val_up = data_ser.quantile(0.75) + iqr
rule_low = (data_ser < val_low)
rule_up = (data_ser > val_up)
# print(rule_low,'_'*10)
return (rule_low, rule_up), (val_low, val_up)
data_n = data.copy()
data_series = data_n[col_name]
rule, value = box_plot_outliers(data_series, box_scale=scale)
index = np.arange(data_series.shape[0])[rule[0] | rule[1]] #获取异常值的索引
#print(index,'='*10)
print("Delete number is: {}".format(len(index)))
data_n = data_n.drop(index) #按照索引删除异常值
data_n.reset_index(drop=True, inplace=True) #还原索引,从新变为默认的整型索引
print("Now column number is: {}".format(data_n.shape[0]))
index_low = np.arange(data_series.shape[0])[rule[0]] #获取低于下限的索引
outliers = data_series.iloc[index_low] #将索引对应的元素取出来
print("Description of data less than the lower bound is:")
print(pd.Series(outliers).describe())
index_up = np.arange(data_series.shape[0])[rule[1]]
outliers = data_series.iloc[index_up]
print("Description of data larger than the upper bound is:")
#print(pd.Series(outliers))
print(pd.Series(outliers).describe())
#绘制箱线图
fig, ax = plt.subplots(1, 2, figsize=(10, 7))
sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
return data_n
# 我们可以删掉一些异常数据,以 power 为例。
# 这里删不删同学可以自行判断
# 但是要注意 test 的数据不能删 = = 不能掩耳盗铃是不是
train_data = outliers_proc(train_data, 'power', scale=3)
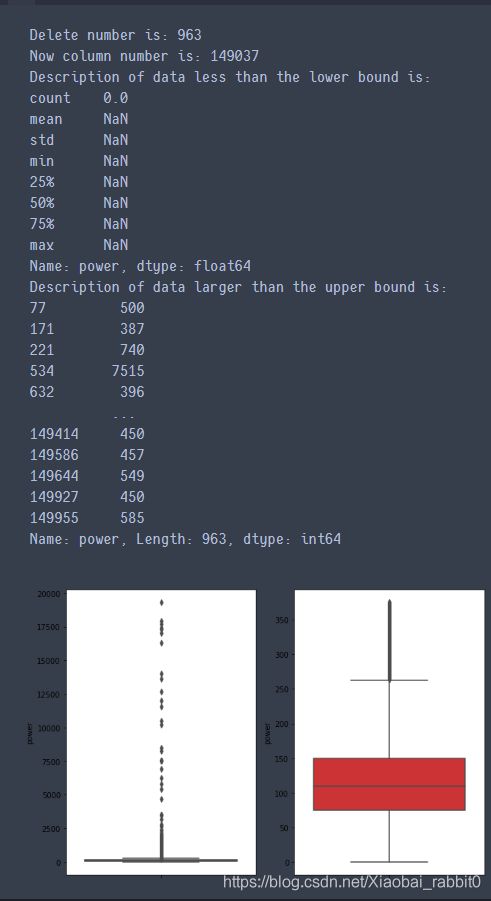
这个代码是直接删除数据,这个如果要使用,不要对测试集用哈。下面看看power这个特征的分布:
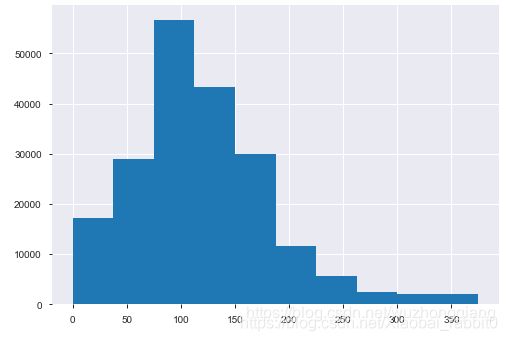
也不错了,所以就没再进一步处理power,至于其他的数值型是不是需要截尾,这个看自己吧。
=================================================================
2.3 删除无用特征
#sell、offerType数据倾斜严重
#删v_1留v_6,删v_2留v_0
del train_data["seller"]
del train_data["offerType"]
del train_data["v_1"]
del train_data["v_2"]
#‘-’也为空缺值,因为很多模型对nan有直接的处理,这里先给替换成nan
train_data['notRepairedDamage'].replace('-',np.nan,inplace=True)
train_data['notRepairedDamage'].value_counts()
train_data.isnull().sum()
# nan可视化
missing = train_data.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()
2.4 缺失值填充
上图可以看到缺失情况, 都是类别特征的缺失,notRepaired这个特征的缺失比较严重, 可以尝试填充, 但目前关于类别缺失,感觉下面的方式都不太好,用模型预测填充比较不错,后期再说吧,因为后面的树模型可以自行处理缺失。 当然OneHot的时候,会把空值处理成全0的一种表示,类似于一种新类型了。
所以,这里先不用处理缺失值
#删除重复值 data.drop_duplicates()
#dropna()可以直接删除缺失样本,但是有点不太好
#填充固定值 train_data.fillna(0, inplace=True) # 填充 0 data.fillna({0:1000, 1:100, 2:0, 4:5}) # 可以使用字典的形式为不同列设定不同的填充值
train_data.fillna(train_data.mean(),inplace=True) # 填充均值 train_data.fillna(train_data.median(),inplace=True) # 填充中位数 train_data.fillna(train_data.mode(),inplace=True) # 填充众数
train_data.fillna(method='pad', inplace=True) # 填充前一条数据的值,但是前一条也不一定有值 train_data.fillna(method='bfill', inplace=True) # 填充后一条数据的值,但是后一条也不一定有值
"""插值法:用插值法拟合出缺失的数据,然后进行填充。"""
for f in features: train_data[f] = train_data[f].interpolate()
train_data.dropna(inplace=True)
"""填充KNN数据:先利用knn计算临近的k个数据,然后填充他们的均值"""
from fancyimpute import KNN train_data_x = pd.DataFrame(KNN(k=6).fit_transform(train_data_x), columns=features)
2.5 特征构造
# 训练集和测试集放在一起,方便构造特征
train_data['train']=1
test_data['train']=0
data = pd.concat([train_data, test_data], ignore_index=True)
1、创造汽车使用时间特征
# 使用时间:data['creatDate'] - data['regDate'],反应汽车使用时间,一般来说价格与使用时间成反比
# 不过要注意,数据里有时间出错的格式,所以我们需要 errors='coerce'
data['used_time'] = (pd.to_datetime(data['creatDate'], format='%Y%m%d', errors='coerce') -
pd.to_datetime(data['regDate'], format='%Y%m%d', errors='coerce')).dt.days
# 看一下空数据,有 15k 个样本的时间是有问题的,我们可以选择删除,也可以选择放着。
# 但是这里不建议删除,因为删除缺失数据占总样本量过大,7.5%
# 我们可以先放着,因为如果我们 XGBoost 之类的决策树,其本身就能处理缺失值,所以可以不用管;
data['used_time'].isnull().sum()
print(data['regionCode'])
这里用到了先验知识,(因为数据来源于德国)德国邮编一般都是五位,前2位代表省份或州别(城市),后3位数表示乡镇数据。所以,我们取后三位之前的数据作为,城市(city)特征。
# 从邮编中提取城市信息,相当于加入了先验知识
data['city'] = data['regionCode'].apply(lambda x : str(x)[:-3])
data = data
# 计算某品牌的销售统计量,同学们还可以计算其他特征的统计量
# 这里要以 train 的数据计算统计量
train_gb = train_data.groupby("brand")
all_info = {}
for kind, kind_data in train_gb:
info = {}
kind_data = kind_data[kind_data['price'] > 0]
info['brand_amount'] = len(kind_data)
info['brand_price_max'] = kind_data.price.max()
info['brand_price_median'] = kind_data.price.median()
info['brand_price_min'] = kind_data.price.min()
info['brand_price_sum'] = kind_data.price.sum()
info['brand_price_std'] = kind_data.price.std()
info['brand_price_average'] = round(kind_data.price.sum() / (len(kind_data) + 1), 2)
all_info[kind] = info
brand_fe = pd.DataFrame(all_info).T.reset_index().rename(columns={"index": "brand"})
data = data.merge(brand_fe, how='left', on='brand')
这里给出groupby函数的详细链接pandas之groupby详解
DataFrame修改index、columns名的方法
Pandas-连接合并函数merge()
2.6 数据分桶
连续值经常离散化或者分离成“箱子”进行分析, 为什么要做数据分桶呢?
分区提供了一个隔离数据和优化查询的便利方式,不过并非所有的数据都可形成合理的分区,尤其是需要确定合适大小的分区划分方式,(不合理的数据分区划分方式可能导致有的分区数据过多,而某些分区没有什么数据的尴尬情况)
好处:
1、方便抽样
2、提高join查询效率
(1)获得更高的查询处理效率。桶为表加上了额外的结构,Hive 在处理有些查询时能利用这个结构。具体而言,连接两个在(包含连接列的)相同列上划分了桶的表,可以使用 Map 端连接 (Map-side join)高效的实现。比如JOIN操作。对于JOIN操作两个表有一个相同的列,如果对这两个表都进行了桶操作。那么将保存相同列值的桶进行JOIN操作就可以,可以大大较少JOIN的数据量。
(2)使取样(sampling)更高效。在处理大规模数据集时,在开发和修改查询的阶段,如果能在数据集的一小部分数据上试运行查询,会带来很多方便。
当然还有很多原因,LightGBM 在改进 XGBoost 时就增加了数据分桶,增强了模型的泛化性
数据分桶的方式:
- 等频分桶
- 等距分桶
- Best-KS分桶(类似利用基尼指数进行二分类)
- 卡方分桶
最好是数据分桶的特征作为新一列的特征,不要把原来的数据给替换掉, 所以在这里通过分桶的方式做一个特征出来看看,以power为例
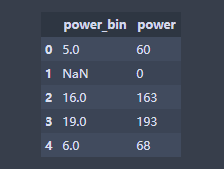
"""下面以power为例进行分桶, 当然构造一列新特征了"""
bin = [i*10 for i in range(31)]
data['power_bin'] = pd.cut(data['power'], bin, labels=False)
data[['power_bin', 'power']].head()
ps:数据分桶的其他例子(迁移之用)
# 连续值经常离散化或者分离成“箱子”进行分析。
# 假设某项研究中一组人群的数据,想将他们进行分组,放入离散的年龄框中
ages = [20, 22, 25, 27, 21, 23, 37, 31, 61, 45, 41, 32]
# 如果按年龄分成18-25, 26-35, 36-60, 61以上的若干组,可以使用pandas中的cut
bins = [18, 25, 35, 60, 100] # 定义箱子的边
cats = pd.cut(ages, bins)
print(cats) # 这是个categories对象 通过bin分成了四个区间, 然后返回每个年龄属于哪个区间
# codes属性
print(cats.codes) # 这里返回一个数组,指明每一个年龄属于哪个区间
print(cats.categories)
print(pd.value_counts(cats)) # 返回结果是每个区间年龄的个数
# 与区间的数学符号一致, 小括号表示开放,中括号表示封闭, 可以通过right参数改变
print(pd.cut(ages, bins, right=False))
# 可以通过labels自定义箱名或者区间名
group_names = ['Youth', 'YonngAdult', 'MiddleAged', 'Senior']
data = pd.cut(ages, bins, labels=group_names)
print(data)
print(pd.value_counts(data))
# 如果将箱子的边替代为箱子的个数,pandas将根据数据中的最小值和最大值计算出等长的箱子
data2 = np.random.rand(20)
print(pd.cut(data2, 4, precision=2)) # precision=2 将十进制精度限制在2位
# qcut是另一个分箱相关的函数, 基于样本分位数进行分箱。 取决于数据的分布,使用cut不会使每个箱子具有相同数据数量的数据点,而qcut,使用
# 样本的分位数,可以获得等长的箱
data3 = np.random.randn(1000) # 正太分布
cats = pd.qcut(data3, 4)
print(pd.value_counts(cats))
删除不需要的数据
# 删除不需要的数据
data = data.drop(['creatDate', 'regDate', 'regionCode'], axis=1)
print(data.shape)
data.columns
Note:目前为止共删掉7个特征(seeller、offerType、v_1、v_2、creatDate、regDate、regionCode)
# 目前的数据其实已经可以给树模型使用了,所以我们导出一下
data.to_csv('data_for_tree.csv', index=0)
我们可以再构造一份特征给 LR NN 之类的模型用,之所以分开构造是因为,不同模型对数据集的要求不同
# 我们可以再构造一份特征给 LR NN 之类的模型用
# 之所以分开构造是因为,不同模型对数据集的要求不同
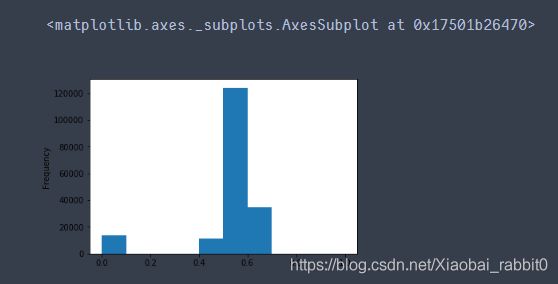
# 我们看下数据分布:
data['power'].plot.hist()
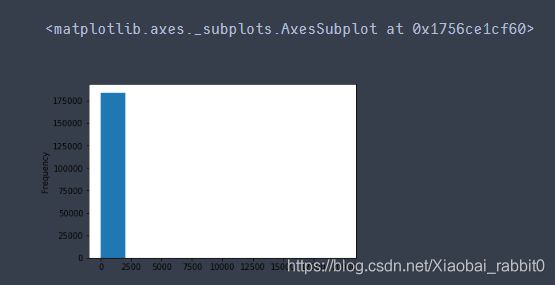
我们刚刚已经对 train 进行异常值处理了,但是现在还有这么奇怪的分布是因为 test 中的 power 异常值,所以我们其实刚刚 train 中的 power 异常值不删为好,可以用长尾分布截断来代替
# 我们刚刚已经对 train 进行异常值处理了,但是现在还有这么奇怪的分布是因为 test 中的 power 异常值,
# 所以我们其实刚刚 train 中的 power 异常值不删为好,可以用长尾分布截断来代替
train_data['power'].plot.hist()
# 我们对其先取 log,再做归一化
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
data['power'] = np.log(data['power'] + 1)
data['power'] = ((data['power'] - np.min(data['power'])) / (np.max(data['power']) - np.min(data['power'])))
data['power'].plot.hist()
# km 的比较正常,应该是已经做过分桶了
data['kilometer'].plot.hist()
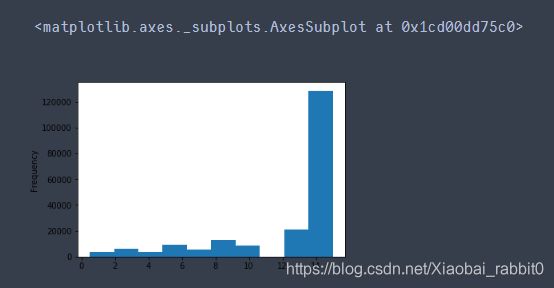
km 的比较正常,应该是已经做过分桶了,所以我们可以直接做归一化
# 所以我们可以直接做归一化
data['kilometer'] = ((data['kilometer'] - np.min(data['kilometer'])) /
(np.max(data['kilometer']) - np.min(data['kilometer'])))
data['kilometer'].plot.hist()

除此之外 还有我们刚刚构造的统计量特征
因为’brand_amount’, ‘brand_price_average’, ‘brand_price_max’,‘brand_price_median’, ‘brand_price_min’, ‘brand_price_std’,'brand_price_sum’等一些特征都服从长尾分布,所以先取对数,再做归一化处理
data['brand_amount'] = np.log(data['brand_amount'] + 1)
data['brand_price_average'] = np.log(data['brand_price_average'] + 1)
data['brand_price_max'] = np.log(data['brand_price_max'] + 1)
data['brand_price_median'] = np.log(data['brand_price_median'] + 1)
data['brand_price_min'] = np.log(data['brand_price_min'] + 1)
data['brand_price_std'] = np.log(data['brand_price_std'] + 1)
data['brand_price_sum'] = np.log(data['brand_price_sum'] + 1)
# 除此之外 还有我们刚刚构造的统计量特征:
# 'brand_amount', 'brand_price_average', 'brand_price_max',
# 'brand_price_median', 'brand_price_min', 'brand_price_std',
# 'brand_price_sum'
# 这里不再一一举例分析了,直接做变换,
def max_min(x):
return (x - np.min(x)) / (np.max(x) - np.min(x))
data['brand_amount'] = ((data['brand_amount'] - np.min(data['brand_amount'])) /
(np.max(data['brand_amount']) - np.min(data['brand_amount'])))
data['brand_price_average'] = ((data['brand_price_average'] - np.min(data['brand_price_average'])) /
(np.max(data['brand_price_average']) - np.min(data['brand_price_average'])))
data['brand_price_max'] = ((data['brand_price_max'] - np.min(data['brand_price_max'])) /
(np.max(data['brand_price_max']) - np.min(data['brand_price_max'])))
data['brand_price_median'] = ((data['brand_price_median'] - np.min(data['brand_price_median'])) /
(np.max(data['brand_price_median']) - np.min(data['brand_price_median'])))
data['brand_price_min'] = ((data['brand_price_min'] - np.min(data['brand_price_min'])) /
(np.max(data['brand_price_min']) - np.min(data['brand_price_min'])))
data['brand_price_std'] = ((data['brand_price_std'] - np.min(data['brand_price_std'])) /
(np.max(data['brand_price_std']) - np.min(data['brand_price_std'])))
data['brand_price_sum'] = ((data['brand_price_sum'] - np.min(data['brand_price_sum'])) /
(np.max(data['brand_price_sum']) - np.min(data['brand_price_sum'])))
one-hot编码的优点
- 离散后稀疏向量内积乘法运算速度更快,计算结果也方便存储,容易扩展;
- 离散后的特征对异常值更具鲁棒性,如 age>30 为 1 否则为 0,对于年龄为 200 的也不会对模型造成很大的干扰;
- LR 属于广义线性模型,表达能力有限,经过离散化后,每个变量有单独的权重,这相当于引入了非线性,能够提升模型的表达能力,加大拟合;
- 离散后特征可以进行特征交叉,提升表达能力,由 M+N 个变量变成 M*N 个变量,进一步引入非线性,提升了表达能力;
- 特征离散后模型更稳定,如用户年龄区间,不会因为用户年龄长了一岁就变化。
LR不支持直接使用类型数据,所以要先对类别进行One-Hot编码
# 对类别特征进行 OneEncoder
data = pd.get_dummies(data, columns=['model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'power_bin'])
print(data.shape)
data.columns
# 这份数据可以给 LR 用
data.to_csv('data_for_lr.csv', index=0)
2.7 特征筛选
2.7.1 过滤式
这里没有使用皮尔逊相关系数,因为皮尔逊相关系数要求数据,服从正态分布,所以使用斯皮尔曼等级相关系数
Spearman介绍
# 相关性分析
#这里没有使用皮尔逊相关系数,因为皮尔逊相关系数要求数据,服从正态分布
#所以使用斯皮尔曼等级相关系数
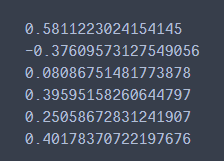
print(data['power'].corr(data['price'], method='spearman'))
print(data['kilometer'].corr(data['price'], method='spearman'))
print(data['brand_amount'].corr(data['price'], method='spearman'))
print(data['brand_price_average'].corr(data['price'], method='spearman'))
print(data['brand_price_max'].corr(data['price'], method='spearman'))
print(data['brand_price_median'].corr(data['price'], method='spearman'))
# 当然也可以直接看图
data_numeric = data[['power', 'kilometer', 'brand_amount', 'brand_price_average',
'brand_price_max', 'brand_price_median']]
correlation = data_numeric.corr()
f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True, vmax=0.8)
这里说明一下,其实给出热图没什么大用处,说白了就是为了好看,因为看相关性,我们直接看上段代码输出的相关性数据更直观。但是竞赛之类的论文里面加上图,那可就是大大大的加分项了,毕竟图少的论文不是好论文,毕竟好看,毕竟看起来舒服,毕竟…
2.7.2 嵌入式
嵌入式是主要方法,三天后,见下篇文章,待更新…
2.8 经验总结
特征工程是比赛中最至关重要的的一块,特别是传统的比赛,大家的模型可能都差不多,调参带来的效果增幅是非常有限的,但特征工程的好坏往往会决定了最终的排名和成绩。
特征工程的主要目的还是在于将数据转换为能更好地表示潜在问题的特征,从而提高机器学习的性能。比如,异常值处理是为了去除噪声,填补缺失值可以加入先验知识等。
特征构造也属于特征工程的一部分,其目的是为了增强数据的表达。
有些比赛的特征是匿名特征,这导致我们并不清楚特征相互直接的关联性,这时我们就只有单纯基于特征进行处理,比如装箱,groupby,agg 等这样一些操作进行一些特征统计,此外还可以对特征进行进一步的 log,exp 等变换,或者对多个特征进行四则运算(如上面我们算出的使用时长),多项式组合等然后进行筛选。由于特性的匿名性其实限制了很多对于特征的处理,当然有些时候用 NN 去提取一些特征也会达到意想不到的良好效果。
对于知道特征含义(非匿名)的特征工程,特别是在工业类型比赛中,会基于信号处理,频域提取,丰度,偏度等构建更为有实际意义的特征,这就是结合背景的特征构建,在推荐系统中也是这样的,各种类型点击率统计,各时段统计,加用户属性的统计等等,这样一种特征构建往往要深入分析背后的业务逻辑或者说物理原理,从而才能更好的找到 magic。
当然特征工程其实是和模型结合在一起的,这就是为什么要为 LR NN 做分桶和特征归一化的原因,而对于特征的处理效果和特征重要性等往往要通过模型来验证。
总的来说,特征工程是一个入门简单,但想精通非常难的一件事。
2.9 Q&A 来自Datawhale答疑
Note:下一章介绍,Lasso 回归和决策树可以完成嵌入式特征选择 大部分情况下都是用“嵌入式”做“特征筛选”
敬请期待…