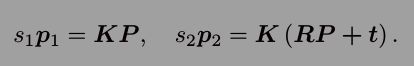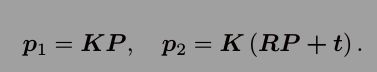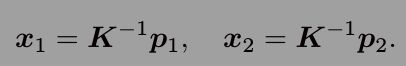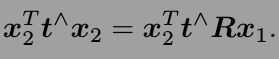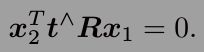slam入门3：2D-2D对极几何中的对极约束公式详细解释（参考 视觉slam十四讲）

声明：下面一些内容引用了高翔的视觉slam十四讲， 感谢作者。

对于我这种刚入门的小白（cai bi）来说，对极约束公式中的某些步骤理解起来还是有些难度的，下面把个人对相关内容的理解写下来，以备日后翻阅。

一、对极约束推导

以下图为例,我们希望求取两帧图像 I1 , I2 之间的运动,设第一帧到第二帧的运动为R, t。两个相机中心分别为 O1 , O2 。现在,考虑 I1 中有一个特征点 p1 ,它在 I2 中对应着特征点 p2 。

图1

从代数角度来看一下这里出现的几何关系。在第一帧的坐标系下,设 P 的空间位置为:

公式1

根据针孔相机模型,我们知道两个像素点 p1 , p2 的像素位置为:

公式2

这里 K 为相机内参矩阵,R, t 为两个坐标系的相机运动。如果使用齐次坐标, 也可以把上式写成在乘以非零常数下成立的(up
to a scale)等式：

公式3

问题（1）来了：为什么使用齐次坐标，并且乘以非零常数后等式依然成立。

解释如下：说到齐次坐标，就要提一下投影几何（或射影几何）。首先齐次坐标是指一个用于投影几何里的坐标系统，如同用于欧式几何里的笛卡儿坐标一般（具体见wiki），射影几何研究在摄影变换下不变的几何性质（具体见wiki）。以针孔相机模型为例，来解释一下为什么齐次坐标乘以非零常数后仍然表示同一个点，如下图：

上图中，O表示相机光心，为像素坐标系下的点，P1，P2，P3为在相机坐标系下的空间点，并且P1，P2，P3均投影到像素坐标系下的p点。在推导相机的内参矩阵时，为了使等式左右两边维度相同，我们把写成齐次坐标形式，如下式：

                                                                        

所以对于P1，P2，P3三点与齐次坐标的关系为：

                                                 Z1 * p = K * P1； Z2 * p = K * P2； Z3 * p = K * P3

则 p =  (K * P1 ) / Z1 = (K * P2 ) / Z2 = (K * P3 ) / Z3， 我们发现，齐次坐标乘以非零常数后依然表示同一个投影点，只不过空间点P位置变了，但都在 这条射线上，齐次坐标乘以不同的非零常数表示不同距离的空间点在像素平面的投影，就是这条射线上的点均投影到 p 点。这也表明了单目相机的一张图像没法确定深度。另外也可参考另一个博客。

由以上解释可以看出，使用齐次坐标可以使相机模型计算更加方便，灵活性更高，乘以非零常数后仍表示同一个点。

接上面的公式3，令

公式4

很明显， 是上面图1中两个像素点  的相机归一化平面上的坐标（相机坐标系下）。

则将公式4带入公式3中，得到： , ， 最终得到：

公式5

两边同时左乘 ，得到：

公式6

两侧同时左乘，得到：

公式7

由于，所以有：

公式8

重新代入，得到：

公式9

这两个式子都称为对极约束。通过定义基础矩阵F和本质矩阵E进一步简化上式：

公式10

E 和 F 只相差了相机内参，求出E或者F就可以通过分解求出R和t。通常内参是已知的，求解E会更方便。

二、本质矩阵

根据定义，本质矩阵，它是一个 3 × 3 的矩阵,内有 9 个未知数。E满足如下条件：

（1）E满足对极约束： ，由于对极约束是等式为零的约束，所以对 E 乘以任意非零常数后，对极约束依然满足，这称为 E 在不同尺度下是等价的，即尺度等价性。

（2）根据， 可以证明，本质矩阵 E 的奇异值必定是 [σ, σ, 0]T 的形式。这称为本质矩阵的内在性质。（推导可见另一博客）

（3）另一方面,由于平移和旋转各有三个自由度，故共有六个自由度。但由于尺度等价性,故 E 实际上有五个自由度。

E的求解：

E 具有五个自由度的事实,表明我们最少可以用五对点来求解 E。但是，E 的内在性质是一种非线性性质,在求解线性方程时会带来麻烦。

问题（2）：本质矩阵E为什么是尺度等价的？

问题（3）：本质矩阵E的奇异值为什么是 [σ, σ, 0]T，怎么求？

问题（4）：本质矩阵E为什么有5个自由度？

这三个问题的答案墙裂推荐一篇有道云笔记（备用链接），该笔记从最基础的矩阵理论出发，一步步解释了本质矩阵、基础矩阵以及单应矩阵的性质和求解方法，新手必备。