Robotics System Toolbox 使用笔记(个人笔记)
Robotics System Toolbox 使用笔记
- 1. 机器人建模
- 2. 设置当前关节配置并获取关节轴数
- 3. 查看并设置工具坐标系
- 4. 获取某一姿态下的齐次变换矩阵
- 5. 生成齐次变换矩阵
- 6. 任务空间轨迹的生成
- 7. 逆运动学
- 8. 关节空间插值
- 9.[轨迹生成函数/simulink模块](https://ww2.mathworks.cn/help/robotics/trajectory-generation.html)
- 9. [坐标变换](https://ww2.mathworks.cn/help/robotics/coordinate-system-transformations.html)
- 10. 逆运动学
- 11. 碰撞检测
- 12. 机器人建模与仿真
环境: MATLAB R2019b
1. 机器人建模
第一种:导入法
- step1:建议直接通过SolidWorks导出urdf文件
- step2:导入urdf文件,
robot_name = import('file_name.urdf') - step3:显示机器人,
show(robot_name)
第二种:加载法(适合工具箱中已有机器人)
robot = loadrobot('kinovaGen3','DataFormat','row','Gravity',[0 0 -9.81]);
2. 设置当前关节配置并获取关节轴数
- 设置当前关节配置:
currentRobotJConfig = homeConfiguration(robot_name) - 获得关节轴数:
numJoints = numel(currentRobotJConfig);
3. 查看并设置工具坐标系
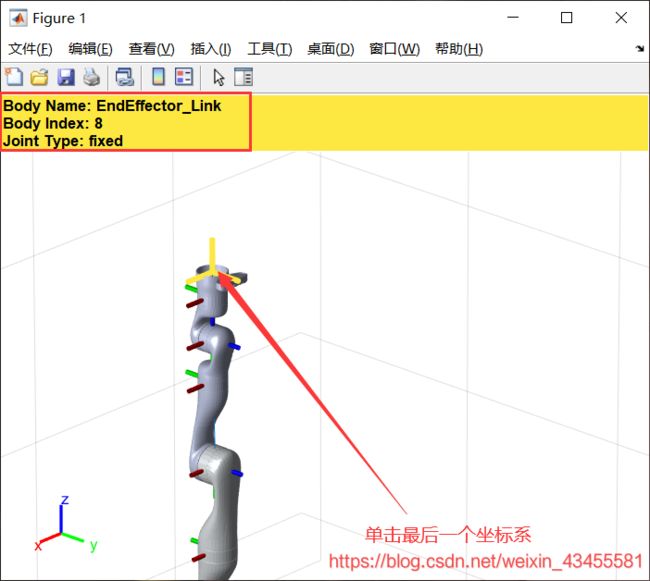
endEffector = "EndEffector_Link";
4. 获取某一姿态下的齐次变换矩阵
- tf = getTransform(tftree,targetframe,sourceframe)
- tf = getTransform(tftree,targetframe,sourceframe,sourcetime)
- tf = getTransform(___,“Timeout”,timeout)
- tf = getTransform(bagSel,targetframe,sourceframe)
- tf = getTransform(bagSel,targetframe,sourceframe,sourcetime)
例:taskInit = getTransform(robot_name,jointInit,endEffector) %获取jointInit位姿下的到末端的齐次变换矩阵
T07 = getTransform(robot_name,home,'link7') %获取home位姿下连杆坐标系7到基坐标系的齐次变换矩阵
5. 生成齐次变换矩阵
jointInit = currentRobotJConfig;
taskInit = getTransform(robot,jointInit,endEffector);
taskFinal = trvec2tform([0.4,0,0.6])*axang2tform([0 1 0 pi]);
6. 任务空间轨迹的生成
-
step1:求欧氏距离,
distance = norm(tform2trvec(taskInit)-tform2trvec(taskFinal)) -
step2:根据行进距离和所需工具坐标的速度定义轨迹时间
timeStep = 0.1;%秒,时间插值步长 toolSpeed = 0.1;% m/s ,工具坐标速度 initTime = 0; % 起始时间 finalTime = (distance/toolSpeed) - initTime;% 计算运行时间 trajTimes = initTime:timeStep:finalTime; % 插值时间 timeInterval = [trajTimes(1); trajTimes(end)]; % 起始时间区间 -
step3:插值计算中间任务空间航路点
[tforms,vel,acc] = transformtraj(T0,TF,时间区间,时间样本)
[tforms,vel,acc] = transformtraj(T0,TF,tInterval,tSamples,Name,Value)
例:[taskWaypoints,taskVelocities] = transformtraj(taskInit,taskFinal,timeInterval,trajTimes)
返回的tforms是中间插值点的齐次变换矩阵形式,返回的速度和加速度是每个关节的关节速度和加速度
7. 逆运动学
-
ik = inverseKinematics
-
ik = inverseKinematics(Name,Value)
-
[configSol,solInfo] = ik(endeffector,pose,weights,initialguess)
-
step1:为机器人创建一个逆运动学对象
ik = inverseKinematics('RigidBodyTree',robot); % rigidBodyTree根据关节之间的转换在机器人模型中指定机器人运动学约束。 ik.SolverParameters.AllowRandomRestart = false; weights = [1 1 1 1 1 1]; -
step2:使用逆运动学计算初始和所需的关节配置
initialGuess = wrapToPi(jointInit); jointFinal = ik(endEffector,taskFinal,weights,initialGuess); jointFinal = wrapToPi(jointFinal);
8. 关节空间插值
-
使用三次多项式函数在它们之间进行插值以生成均匀间隔的关节配置的数组,使用B样条曲线生成平滑的轨迹
ctrlpoints = [jointInit',jointFinal']; jointConfigArray = cubicpolytraj(ctrlpoints,timeInterval,trajTimes); jointWaypoints = bsplinepolytraj(jointConfigArray,timeInterval,1);
9.轨迹生成函数/simulink模块
| 函数 | 说明 |
|---|---|
| bsplinepolytraj | 使用B样条生成多项式轨迹 |
| cubicpolytraj | 生成三阶多项式轨迹 |
| quinticpolytraj | 生成五阶轨迹 |
| rottraj | 生成方向旋转矩阵之间的轨迹 |
| transformtraj | 在两个转换之间生成轨迹 |
| trapveltraj | 生成具有梯形速度轮廓的轨迹 |
| 模块名称 | 说明 |
|---|---|
| Polynomial Trajectory | 通过航路点生成多项式轨迹 |
| Rotation Trajectory | 生成两个方向之间的轨迹 |
| Transform Trajectory | 在两个齐次变换之间生成轨迹 |
| Trapezoidal Velocity Profile Trajectory | 使用梯形速度轮廓通过多个航路点生成轨迹 |
9. 坐标变换
| 函数 | 说明 |
|---|---|
| axang2quat | 将轴角旋转转换为四元数 |
| axang2rotm | 将轴角旋转转换为旋转矩阵 |
| axang2tform | 将轴角旋转转换为均匀变换 |
| eul2quat | 将欧拉角转换为四元数 |
| eul2rotm | 将欧拉角转换为旋转矩阵 |
| eul2tform | 将欧拉角转换为均匀变换 |
| quat2axang | 将四元数转换为轴角旋转 |
| quat2eul | 将四元数转换为欧拉角 |
| quat2rotm | 将四元数转换为旋转矩阵 |
| quat2tform | 将四元数转换为齐次变换 |
| quaternion | 创建一个四元数数组 |
| rotm2axang | 将旋转矩阵转换为轴角旋转 |
| rotm2eul | 将旋转矩阵转换为欧拉角 |
| rotm2quat | 将旋转矩阵转换为四元数 |
| rotm2tform | 将旋转矩阵转换为齐次变换 |
| tform2axang | 将齐次变换转换为轴角旋转 |
| tform2eul | 从齐次变换中提取欧拉角 |
| tform2quat | 从齐次变换中提取四元数 |
| tform2rotm | 从齐次变换中提取旋转矩阵 |
| tform2trvec | 从齐次变换中提取平移向量 |
| angdiff | 两个角度之间的差异 |
| cart2hom | 将笛卡尔坐标转换为齐次坐标 |
| hom2cart | 将齐次坐标转换为笛卡尔坐标 |
| trvec2tform | 将平移向量转换为齐次变换 |
10. 逆运动学
https://ww2.mathworks.cn/help/robotics/inverse-kinematics.html
11. 碰撞检测
https://ww2.mathworks.cn/help/robotics/collision-detection.html
12. 机器人建模与仿真
https://ww2.mathworks.cn/help/robotics/modeling-and-simulation.html
参考文献:
https://ww2.mathworks.cn/help/robotics/examples/plan-and-execute-trajectory-kinova-gen3.html
https://ww2.mathworks.cn/help/robotics/index.html?s_tid=CRUX_lftnav

