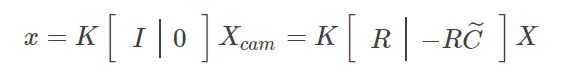- 全网最简单实用Android平板USB摄像头开发,同时预览多个摄像头,双目摄像头,同时打开手机前后摄像头(红外摄像头、人脸识别、活体检测、Android Camer
云启软件
Android原生笔记
老规矩,先视频8月20日背景:多摄像头有很多实现方案,手机上能实现跑通,但是Android平板USB的找了好久才实现,需要低版本API,废话不多说直接代码:工具类importandroid.graphics.SurfaceTexture;importandroid.hardware.Camera;importandroid.view.TextureView;importjava.io.IOExce
- (无人驾驶之二)感知层的传感器---LIDAR、GPS、惯性传感器、双目摄像头
abiggg
无人驾驶AI传感器摄像头gps无人机系统
一、LIDAR(光雷达)1.1原理激光雷达对物体距离的测量与通常所说的雷达类似,都是通过测量发送和接受到的脉冲信号的时间间隔来计算物体的距离。因此,由于原理上的相似性,尽管雷达的准确定义是使用微波或无线电波等波长较长的电磁波进行检测测距的设备,激光雷达这一术语仍然被广泛使用。1.2优点与传统雷达相比:采用激光测矩,波长在600~1000nm,测量更加精准,可达厘米级别;可感知物体矩离及表面形状;1
- 科普类—— 双目视觉系统在无人驾驶汽车中的安装位置(四)
JANGHIGH
科普类无人驾驶汽车人工智能计算机视觉
科普类——双目视觉系统在无人驾驶汽车中的安装位置(四)在无人驾驶汽车中,双目视觉系统的安装位置和两个相机之间的安装间距(基线)对于系统的性能至关重要。这些参数的选择需要基于工程数据和实际应用需求来确定。以下是一些关于双目视觉系统安装位置和间距的一般指导原则:安装位置:双目摄像头通常安装在车辆的前部,以模拟人类驾驶员的视线。它们应该位于车辆的中心线附近,以确保视野覆盖车辆前方的主要区域。安装高度通常
- 车辆网行业术语合集
Ad大成
最近在研究专利的问题,阅读了许多专利,发现好多的术语都不知道,特在此记录一下,方便以后查阅和个人记忆。ADAS高级驾驶辅助系统(AdvancedDrivingAssistanceSystem)是利用安装在车上的各式各样传感器(毫米波雷达、激光雷达、单\双目摄像头以及卫星导航),在汽车行驶过程中随时来感应周围的环境,收集数据,进行静态、动态物体的辨识、侦测与追踪,并结合导航地图数据,进行系统的运算与
- 生物识别规划人脸识别芯片方案的概述和特点
weixin_45260069
航芯人工智能人脸识别单片机嵌入式硬件
方案概述人脸识别方案采用高性能AI芯片,支持RGB和IR摄像头,支持LCD显示屏。方案特点•普通RGB摄像头和IR摄像头同时参与3D成像RGB摄像头支持屏幕回显•双目摄像头得到特征点视差计算人脸相对3D深度信息,同时利用可见光和红外光谱信息,活体更难伪造可防止2D图像及高精度3D头模攻击•可根据光线强度,自动调节,适应强光与暗光•90度FOV角度识别•专用低功耗AI芯片,1.2s内解锁,待机功耗低
- 【转】ORB-SLAM2调用OAK-D双目摄像头进行点云建图
OAK中国_官方
OAK深度相机使用教程OAK相机depthaiorb-slam
编辑:OAK中国首发:A.hyh@CSDN喜欢的话,请多多⭐️✍内容来自用户的分享,如有疑问请与原作者交流!▌前言Hello,大家好,这里是OAK中国,我是助手君。近期在CSDN刷到一篇教程,感觉不错的呦,分享给大家!更多资源和教程,可在我的主页搜索哦。▌一、运行stereo_node.launch实例查看双目摄像头发布的话题,并修改orb-slam2摄像头节点。gagaga@ubuntu:~$c
- 生物识别规划人脸识别方案的概述
深圳市青牛科技实业有限公司 小芋圆
芯谷人工智能人脸识别无人机社交电子芯片单片机
方案概述人脸识别方案采用高性能AI芯片,支持RGB和IR摄像头,支持LCD显示屏。方案特点•普通RGB摄像头和IR摄像头同时参与3D成像RGB摄像头支持屏幕回显•双目摄像头得到特征点视差计算人脸相对3D深度信息,同时利用可见光和红外光谱信息,活体更难伪造可防止2D图像及高精度3D头模攻击•可根据光线强度,自动调节,适应强光与暗光•90度FOV角度识别•专用低功耗AI芯片,1.2s内解锁,待机功耗低
- 生物识别规划人脸识别方案的概述和特点
青牛科技-Allen
航芯人工智能人脸识别安全芯片
方案概述人脸识别方案采用高性能AI芯片,支持RGB和IR摄像头,支持LCD显示屏。方案特点•普通RGB摄像头和IR摄像头同时参与3D成像RGB摄像头支持屏幕回显•双目摄像头得到特征点视差计算人脸相对3D深度信息,同时利用可见光和红外光谱信息,活体更难伪造可防止2D图像及高精度3D头模攻击•可根据光线强度,自动调节,适应强光与暗光•90度FOV角度识别•专用低功耗AI芯片,1.2s内解锁,待机功耗低
- 《 机器人基础 》期末试卷(A)
摆烂仙君
机器人
一、填空题(30分,每空2分)1.按照相机的工作方式,机器人常用相机分为1)__单目摄像头2)__双目摄像头_3)_深度摄像头_三类。2.度量地图强调精确地表示地图中物体的位置关系,通常我们用稀疏与稠密对它们进行分类。3.自由度定义为物体能够对坐标系进行独立运动的数目,三维空间中完全确定任意物体的位置和姿态,至少需要__6_____个自由度数目。4.按照运动和观测方程是否为线性,噪声是否服从高斯分
- 三维扫描仪[2]——大恒、微软、还是淘宝一下双目摄像头?
我不想好好敲代码
三维扫描仪双目视觉三维重建双目立体视觉kinect-3d
三维扫描需要怎样的硬件设备?又为什么需要这样的硬件设备?人有两只眼睛所以扫描仪就有两个摄像头?大一时看张广军著《机器视觉》简直要死(实话,大一时高数课上都看C语言去了,只怪当年太天真)…让我们先从光学三角测量开始。不懂什么玩意?从大白天你目测短裙妹子的腿有多长开始……懂了吧!既然是大白天看,光源必不可少。一个良好的光照条件会让整个扫描变得简单。玩过相机的都知道ISO,高ISO会造成高噪点,你讨厌噪
- 【紫光同创国产FPGA教程】【PGL50H第九章】OV5640 双目摄像头实验例程
小眼睛FPGA
fpga开发
本原创教程由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处适用于板卡型号:紫光同创PGL50H开发平台(盘古50K)一:盘古50K开发板(紫光同创PGL50H开发平台)简介盘古50K开发板(紫光同创Logos系列PGL50H关键特性评估板)采用核心板+扩展板的结构,并使用高速板对板连接器进行连接。核心板由FPGA+2颗DDR3+Flash+电源及复位构成,承担FPGA的
- 爱好高科技之人脸识别模块
iowin888
离线语音笔记语音识别人工智能人脸识别活体检测
前段时间看到一款性价比很不错的人脸识别模组,2个关键指标引起了我极大的兴趣:1.99%的识别通过率,误识率低于百万分之一;2.双目摄像头,活体检测。于是买了几个,结合离线语音模块,两者通过串口进行一问一答通信,人机交互部分通过语音和OLED显示进行提示和展现,支持语音设定系统时间,语音报时,多角色注册与识别,如注册爸爸人脸,注册成功后,爸爸人脸凑过去,对模块说一声开始识别,模块能准确的识别出您的身
- Python实现双目标定、畸变矫正、立体矫正
code2035
双目计算机视觉人工智能单目双目
一,双目标定、畸变矫正、立体矫正的作用双目目标定:3D重建和测距:通过双目目标定,您可以确定两个摄像头之间的相对位置和朝向,从而能够根据视差信息计算物体的深度,进行三维重建和测距。姿态估计:双目摄像头可以用于估计物体或相机的姿态,这对于虚拟现实、增强现实和机器人导航等应用非常重要。畸变矫正:图像质量提高:镜头畸变会引入图像失真,畸变矫正可以改善图像质量,使物体的形状更准确。特征匹配:在图像特征匹配
- OpenCV Java入门五 结合摄像头识脸和拍照
TGITCIC
架构师修练之道opencvopencvjava计算机视觉AI人脸识别
随着我们对环境、Mat基本使用越来越熟练、JavaSwing也逐步熟悉了起来。今天我们开始进入OpenCV驱动摄像头的几个使用场景。环境准备准备好一个USB外接摄像头,我这边使用的有两种,一种是普通的罗技摄像头,一种是双目摄像头(将来用来做活检);eclipse2021-12版;JDK11+,因为我们编写swing要使用到WindowBuilder窗体设计器这个插件。在eclipse2021-12
- RK3566 linux调试双目摄像头 同时开启
火柴棍mcu
linux系统及驱动开发linuxrk3566camera
基于RK3566做人脸识别,选用了一款双目摄像头,RGB+IR,RGBSensor为GC2093,IRSensor为GC2053。MIPICSI使用splitmode,可以同时读取两个Sensor的图像。注意事项:一些低版本的SDK无法启用双目摄像头,刚开始使用的内核版本为4.19.193一直无法启用,后来换为内核版本为4.19.232sdk才行。一、硬件连接器件I2C总线及地址:GC2093:I
- opencv 打开双目摄像头只能采集一个摄像头的问题,及左右目图像分割成两幅图
nice-wyh
opencvopencv计算机视觉人工智能
一.opencv打开双目摄像头只能采集一个摄像头的问题本人采用单USB接口的双目摄像头,总是只打开左摄像头的图,经摸索后发现主要就是分辨率的问题,如果分辨率设置正确,便可以打开左右目合成图(在一张图上),如果设置不正确,可能报错,也可能只显示左目图像,所以解决如下intmain(){cv::VideoCapturecap(0);//把path改为0,则读取摄像头cap.set(cv::CAP_PR
- Android开启双摄像头
Charleyszc
Android
开启双目摄像头的需求大部分都会出现在人脸识别的设备上,所以这里的方法仅作为参考。之前写过一篇双目摄像头的文章,但是说的非常笼统,重点的问题都没有提到,今天咱们就来好好说道说道先在activity_main.xml里撸一个布局,两个SurfaceView用来分别显示两个摄像头获取的图像:视频内容显示可以用SurfaceView或TextureView,这两个都可以进行视频画面帧的展示,他们的区别以后
- 14.04 双目摄像头
16_f9b9
若是无头绪,请检查是不是权限问题修改设备文件权限从apt安装,刷新udev:sudoapt-getinstallros-lunar-pointgrey-camera-driver列出检测到的相机rosrunpointgrey_camera_driverlist_cameras发射相机:roslaunchpointgrey_camera_driverbumblebee.launchroslaunch
- 20220330时间轴--双目摄像头
hydro
动机:为何要买摄像头模块?为何要买双目模块而不是?摄像头高分辨率,低价格。用2个摄像头,加视差算法,测量图片中物体与摄像头的距离,输出深度图。用2个摄像头不容易做到图像的同步,所以要哟呵个双目模块,方便左右眼同步行为:CHUSEI双目摄像头,购买日期:2022-02-12CHUSEI双目摄像头参数30万像素UVC协议免驱双目同步,视角60度?45元缺点没有主动光,在环境较暗的时候不工作。行为:HB
- ADAS&APA场景设计分享
怿星科技
HMI设计汽车ADASAPA动效设计HMI
相信大家都对于ADAS与APA这两个车机功能都不陌生,对其场景设计过程可能并不是很清楚。今天小怿就跟大家分享一下自己的设计心得。首先,我们来看一下ADAS和APA的定义,以便我们更好地了解其功能和应用场景。ADAS定义ADAS的全称叫AdvancedDrivingAssistanceSystem(高级驾驶辅助系统)(是利用安装在车上的各式各样传感器(毫米波雷达、激光雷达、单\双目摄像头以及卫星导航
- ubuntu20.04+ROS noetic在线运行单USB双目ORB_SLAM
Julyers
SLAMslamopencv
双目摄像头主要有以下几种,各有优缺点。1.单USB插口,左右图像单独输出2.双USB插口,左右图像单独输出(可能存在同步性问题)3.双USB插口,左右图像合成输出4.单USB插口,左右图像合成输出官方版本的ORBSLAM2编译运行参考之前记录的博客虽然在ubuntu22.04上编译和运行的,但我后来在ubuntu20.04上编译和运行,报错也都差不多,主要是OpenCV的版本问题,由于需要使用RO
- Face X1人脸识别一体机
暴走的阿Sai
开源硬件FireflyRK3399人脸识别人工智能AI
采用RK3399六核64位CPU,配置全铝合金CNC外壳、IPS高端屏幕以及宽动态双目摄像头,拥有强大的人脸识别性能,高效识别,运行稳定可靠,开放配套资料,助力人脸识别项目快速落地。六核64位处理器板载六核64位”服务器级”处理器RK3399,芯片性能强悍,主频高达1.8GHz,集成四核Mali-T860GPU,支持多格式视频编解码,处理性能更出色。高效识别,高准确率流畅适配多种人脸识别算法,高效
- RK3566调试双目摄像头
火柴棍mcu
linux系统及驱动开发linuxcameraRK3566
基于RK3566做人脸识别,选用了一款双目摄像头,RGB+IR,RGBSensor为GC2093,IRSensor为GC2053。MIPICSI使用splitmode,可以同时读取两个Sensor的图像。系统buildroot硬件连接:器件I2C总线及地址:GC2093:I2C2---0x7e(7bitaddress);GC2053:I2C2---0x37(7bitaddress);CSI:GC2
- 使用python-opencv对双目摄像头进行立体视觉图像矫正,去畸变
PureZzzz
opencvpython计算机视觉
准备1、一张棋盘图可以直接从opencv官方github下载,这是一个拥有10*7个格子的棋盘,共有9*6个角点,每个格子24mm,本文所使用的就是这一个棋盘。你需要将它打印在A4纸上用于后续使用。(也可以根据官方教程自行设置棋盘大小OpenCV:Createcalibrationpattern)opencv/pattern.pngat4.x·opencv/opencv·GitHub2、一个双目摄
- 3d重建+神经渲染
noobiee
3D机器学习深度学习3d深度学习图形渲染
3d重建基于深度相机(结构光、TOF、双目摄像头)的三维重建基于图像的三维重建:深度学习基于视觉几何的传统三维重建:这种三维重建方法研究时间比较久远,技术相对成熟。主要通过多视角图像对采集数据的相机位置进行估计,再通过图像提取特征后进行比对拼接完成二维图像到三维模型的转换,就像利用立体几何中的三视图还原立体图一样。3D形状表示方法(shaperepresentation)深度图(depthmap)
- 基于Raspberry Pi和双目摄像头的无人机目标识别、跟踪与实时测距系统开发
应用市场
机器人无人机计算机视觉python
硬件选择:RaspberryPi4:它是一款功能强大的微型计算机,可以轻松地与各种传感器和摄像头配合使用。双目摄像头:例如选择RaspberryPi相容的Arducam双目摄像头,双目摄像头可以捕捉到两个略有差异的图像,这对于空间测距非常重要。算法:使用**立体视觉(StereoVision)**算法来进行空间测距。这个算法基于从两个摄像头捕捉到的图像来计算深度信息。对于目标识别,可以使用深度学习
- ZYNQ ARM+FPGA双目立体视觉控制器设计与实现(一)
深圳信迈科技DSP+ARM+FPGA
ZYNQZYNQ视觉
通过ZYNQ板卡实现FPGA+ARM架构的双目立体视觉系统本设计采用实验室自主开发的Zynq-7020板卡,提出了基于FPGA+ARM架构的双目立体视觉的软硬件系统设计方案。根据对系统软硬件功能划分,PL(FPGA)端主要实现了双目摄像头图像的采集存储和HDMI显示,PS(ARM)端主要实现了软件控制和双目立体视觉立体匹配和立体校正算法。本设计双目摄像头采用OV5640,图像分辨率为640*480
- matlab双目标定误差过大的一些问题
qq_42854129
matlab图像处理
在双目摄像头标定中,使用matlab的自动标定包stereocalibration标定,有的时候会出现达到几十上百的误差,拍了很多组数据都没有特别大的变化。不要着急,这有可能是matlab的对图片的误匹配,即可能第1张匹配到了第10张之类的,或者是应该是第6张对应第7张变成了第7张对应第6张,即左右相机拍照的结果相反了。还有可能是匹配出来的坐标原点不一样,在matlab标定时的左边可以查看(0,0
- YOLO v5与双目测距
@BangBang
objectdetectionopencv人工智能计算机视觉
YOLOv5与双目测距结合,实现目标的识别和定位测距参考1:双目摄像头Matlab参数定标参考2:Python-OpenCV双目测距代码实现以及参数解读
- OpenCV3.2 双目摄像头标定与SGBM算法验证
饮茶先啦靓仔
双目标定的目标在于得出两个摄像头之间的旋转矩阵R(rotationmatrix)和平移向量T(translationvector),以及各自的旋转矩阵RlRr、投影矩阵PlPr和重映射矩阵Q(disparity-to-depthmappingmatrix)。经过立体匹配(BM、SGBM、GC算法等)后可得出视差图,根据Q便可计算出实际空间坐标。跟上一篇一样,后来的我也将这部分的原理总结了一下,可以
- HttpClient 4.3与4.3版本以下版本比较
spjich
javahttpclient
网上利用java发送http请求的代码很多,一搜一大把,有的利用的是java.net.*下的HttpURLConnection,有的用httpclient,而且发送的代码也分门别类。今天我们主要来说的是利用httpclient发送请求。
httpclient又可分为
httpclient3.x
httpclient4.x到httpclient4.3以下
httpclient4.3
- Essential Studio Enterprise Edition 2015 v1新功能体验
Axiba
.net
概述:Essential Studio已全线升级至2015 v1版本了!新版本为JavaScript和ASP.NET MVC添加了新的文件资源管理器控件,还有其他一些控件功能升级,精彩不容错过,让我们一起来看看吧!
syncfusion公司是世界领先的Windows开发组件提供商,该公司正式对外发布Essential Studio Enterprise Edition 2015 v1版本。新版本
- [宇宙与天文]微波背景辐射值与地球温度
comsci
背景
宇宙这个庞大,无边无际的空间是否存在某种确定的,变化的温度呢?
如果宇宙微波背景辐射值是表示宇宙空间温度的参数之一,那么测量这些数值,并观测周围的恒星能量输出值,我们是否获得地球的长期气候变化的情况呢?
&nbs
- lvs-server
男人50
server
#!/bin/bash
#
# LVS script for VS/DR
#
#./etc/rc.d/init.d/functions
#
VIP=10.10.6.252
RIP1=10.10.6.101
RIP2=10.10.6.13
PORT=80
case $1 in
start)
/sbin/ifconfig eth2:0 $VIP broadca
- java的WebCollector爬虫框架
oloz
爬虫
WebCollector主页:
https://github.com/CrawlScript/WebCollector
下载:webcollector-版本号-bin.zip将解压后文件夹中的所有jar包添加到工程既可。
接下来看demo
package org.spider.myspider;
import cn.edu.hfut.dmic.webcollector.cra
- jQuery append 与 after 的区别
小猪猪08
1、after函数
定义和用法:
after() 方法在被选元素后插入指定的内容。
语法:
$(selector).after(content)
实例:
<html>
<head>
<script type="text/javascript" src="/jquery/jquery.js"></scr
- mysql知识充电
香水浓
mysql
索引
索引是在存储引擎中实现的,因此每种存储引擎的索引都不一定完全相同,并且每种存储引擎也不一定支持所有索引类型。
根据存储引擎定义每个表的最大索引数和最大索引长度。所有存储引擎支持每个表至少16个索引,总索引长度至少为256字节。
大多数存储引擎有更高的限制。MYSQL中索引的存储类型有两种:BTREE和HASH,具体和表的存储引擎相关;
MYISAM和InnoDB存储引擎
- 我的架构经验系列文章索引
agevs
架构
下面是一些个人架构上的总结,本来想只在公司内部进行共享的,因此内容写的口语化一点,也没什么图示,所有内容没有查任何资料是脑子里面的东西吐出来的因此可能会不准确不全,希望抛砖引玉,大家互相讨论。
要注意,我这些文章是一个总体的架构经验不针对具体的语言和平台,因此也不一定是适用所有的语言和平台的。
(内容是前几天写的,现附上索引)
前端架构 http://www.
- Android so lib库远程http下载和动态注册
aijuans
andorid
一、背景
在开发Android应用程序的实现,有时候需要引入第三方so lib库,但第三方so库比较大,例如开源第三方播放组件ffmpeg库, 如果直接打包的apk包里面, 整个应用程序会大很多.经过查阅资料和实验,发现通过远程下载so文件,然后再动态注册so文件时可行的。主要需要解决下载so文件存放位置以及文件读写权限问题。
二、主要
- linux中svn配置出错 conf/svnserve.conf:12: Option expected 解决方法
baalwolf
option
在客户端访问subversion版本库时出现这个错误:
svnserve.conf:12: Option expected
为什么会出现这个错误呢,就是因为subversion读取配置文件svnserve.conf时,无法识别有前置空格的配置文件,如### This file controls the configuration of the svnserve daemon, if you##
- MongoDB的连接池和连接管理
BigCat2013
mongodb
在关系型数据库中,我们总是需要关闭使用的数据库连接,不然大量的创建连接会导致资源的浪费甚至于数据库宕机。这篇文章主要想解释一下mongoDB的连接池以及连接管理机制,如果正对此有疑惑的朋友可以看一下。
通常我们习惯于new 一个connection并且通常在finally语句中调用connection的close()方法将其关闭。正巧,mongoDB中当我们new一个Mongo的时候,会发现它也
- AngularJS使用Socket.IO
bijian1013
JavaScriptAngularJSSocket.IO
目前,web应用普遍被要求是实时web应用,即服务端的数据更新之后,应用能立即更新。以前使用的技术(例如polling)存在一些局限性,而且有时我们需要在客户端打开一个socket,然后进行通信。
Socket.IO(http://socket.io/)是一个非常优秀的库,它可以帮你实
- [Maven学习笔记四]Maven依赖特性
bit1129
maven
三个模块
为了说明问题,以用户登陆小web应用为例。通常一个web应用分为三个模块,模型和数据持久化层user-core, 业务逻辑层user-service以及web展现层user-web,
user-service依赖于user-core
user-web依赖于user-core和user-service
依赖作用范围
Maven的dependency定义
- 【Akka一】Akka入门
bit1129
akka
什么是Akka
Message-Driven Runtime is the Foundation to Reactive Applications
In Akka, your business logic is driven through message-based communication patterns that are independent of physical locatio
- zabbix_api之perl语言写法
ronin47
zabbix_api之perl
zabbix_api网上比较多的写法是python或curl。上次我用java--http://bossr.iteye.com/blog/2195679,这次用perl。for example: #!/usr/bin/perl
use 5.010 ;
use strict ;
use warnings ;
use JSON :: RPC :: Client ;
use
- 比优衣库跟牛掰的视频流出了,兄弟连Linux运维工程师课堂实录,更加刺激,更加实在!
brotherlamp
linux运维工程师linux运维工程师教程linux运维工程师视频linux运维工程师资料linux运维工程师自学
比优衣库跟牛掰的视频流出了,兄弟连Linux运维工程师课堂实录,更加刺激,更加实在!
-----------------------------------------------------
兄弟连Linux运维工程师课堂实录-计算机基础-1-课程体系介绍1
链接:http://pan.baidu.com/s/1i3GQtGL 密码:bl65
兄弟连Lin
- bitmap求哈密顿距离-给定N(1<=N<=100000)个五维的点A(x1,x2,x3,x4,x5),求两个点X(x1,x2,x3,x4,x5)和Y(
bylijinnan
java
import java.util.Random;
/**
* 题目:
* 给定N(1<=N<=100000)个五维的点A(x1,x2,x3,x4,x5),求两个点X(x1,x2,x3,x4,x5)和Y(y1,y2,y3,y4,y5),
* 使得他们的哈密顿距离(d=|x1-y1| + |x2-y2| + |x3-y3| + |x4-y4| + |x5-y5|)最大
- map的三种遍历方法
chicony
map
package com.test;
import java.util.Collection;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
public class TestMap {
public static v
- Linux安装mysql的一些坑
chenchao051
linux
1、mysql不建议在root用户下运行
2、出现服务启动不了,111错误,注意要用chown来赋予权限, 我在root用户下装的mysql,我就把usr/share/mysql/mysql.server复制到/etc/init.d/mysqld, (同时把my-huge.cnf复制/etc/my.cnf)
chown -R cc /etc/init.d/mysql
- Sublime Text 3 配置
daizj
配置Sublime Text
Sublime Text 3 配置解释(默认){// 设置主题文件“color_scheme”: “Packages/Color Scheme – Default/Monokai.tmTheme”,// 设置字体和大小“font_face”: “Consolas”,“font_size”: 12,// 字体选项:no_bold不显示粗体字,no_italic不显示斜体字,no_antialias和
- MySQL server has gone away 问题的解决方法
dcj3sjt126com
SQL Server
MySQL server has gone away 问题解决方法,需要的朋友可以参考下。
应用程序(比如PHP)长时间的执行批量的MYSQL语句。执行一个SQL,但SQL语句过大或者语句中含有BLOB或者longblob字段。比如,图片数据的处理。都容易引起MySQL server has gone away。 今天遇到类似的情景,MySQL只是冷冷的说:MySQL server h
- javascript/dom:固定居中效果
dcj3sjt126com
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&
- 使用 Spring 2.5 注释驱动的 IoC 功能
e200702084
springbean配置管理IOCOffice
使用 Spring 2.5 注释驱动的 IoC 功能
developerWorks
文档选项
将打印机的版面设置成横向打印模式
打印本页
将此页作为电子邮件发送
将此页作为电子邮件发送
级别: 初级
陈 雄华 (
[email protected]), 技术总监, 宝宝淘网络科技有限公司
2008 年 2 月 28 日
&nb
- MongoDB常用操作命令
geeksun
mongodb
1. 基本操作
db.AddUser(username,password) 添加用户
db.auth(usrename,password) 设置数据库连接验证
db.cloneDataBase(fromhost)
- php写守护进程(Daemon)
hongtoushizi
PHP
转载自: http://blog.csdn.net/tengzhaorong/article/details/9764655
守护进程(Daemon)是运行在后台的一种特殊进程。它独立于控制终端并且周期性地执行某种任务或等待处理某些发生的事件。守护进程是一种很有用的进程。php也可以实现守护进程的功能。
1、基本概念
&nbs
- spring整合mybatis,关于注入Dao对象出错问题
jonsvien
DAOspringbeanmybatisprototype
今天在公司测试功能时发现一问题:
先进行代码说明:
1,controller配置了Scope="prototype"(表明每一次请求都是原子型)
@resource/@autowired service对象都可以(两种注解都可以)。
2,service 配置了Scope="prototype"(表明每一次请求都是原子型)
- 对象关系行为模式之标识映射
home198979
PHP架构企业应用对象关系标识映射
HELLO!架构
一、概念
identity Map:通过在映射中保存每个已经加载的对象,确保每个对象只加载一次,当要访问对象的时候,通过映射来查找它们。其实在数据源架构模式之数据映射器代码中有提及到标识映射,Mapper类的getFromMap方法就是实现标识映射的实现。
二、为什么要使用标识映射?
在数据源架构模式之数据映射器中
//c
- Linux下hosts文件详解
pda158
linux
1、主机名: 无论在局域网还是INTERNET上,每台主机都有一个IP地址,是为了区分此台主机和彼台主机,也就是说IP地址就是主机的门牌号。 公网:IP地址不方便记忆,所以又有了域名。域名只是在公网(INtERNET)中存在,每个域名都对应一个IP地址,但一个IP地址可有对应多个域名。 局域网:每台机器都有一个主机名,用于主机与主机之间的便于区分,就可以为每台机器设置主机
- nginx配置文件粗解
spjich
javanginx
#运行用户#user nobody;#启动进程,通常设置成和cpu的数量相等worker_processes 2;#全局错误日志及PID文件#error_log logs/error.log;#error_log logs/error.log notice;#error_log logs/error.log inf
- 数学函数
w54653520
java
public
class
S {
// 传入两个整数,进行比较,返回两个数中的最大值的方法。
public
int
get(
int
num1,
int
nu
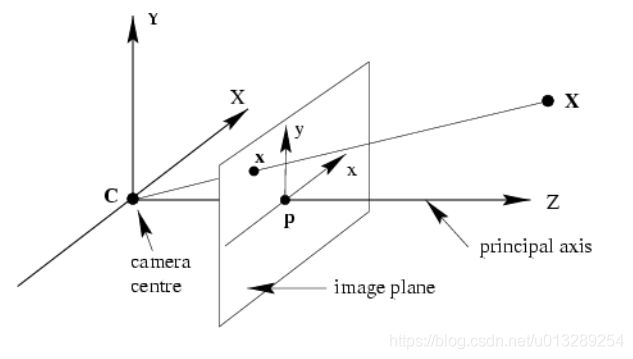
![]() ,其中R表示旋转矩阵,
,其中R表示旋转矩阵,![]() 表示x点在世界坐标系中的位置,
表示x点在世界坐标系中的位置,![]() 表示相机坐标系的原点C在世界坐标系中的位置,
表示相机坐标系的原点C在世界坐标系中的位置,![]() 表示x点在相机坐标系的位置。
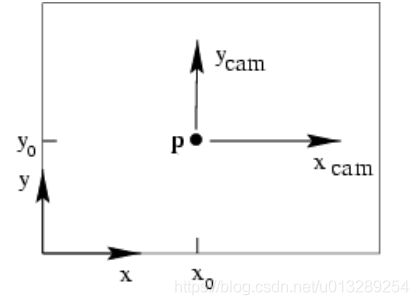
表示x点在相机坐标系的位置。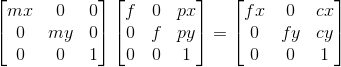 ,其中fx、fy、cx和cy就是相机内参数矩阵得到的四个参数,可以参见我上一篇博客:vs2015 + opencv3 双目摄像头标定(C++实现)
,其中fx、fy、cx和cy就是相机内参数矩阵得到的四个参数,可以参见我上一篇博客:vs2015 + opencv3 双目摄像头标定(C++实现)![]() ,为了方便公式之间的转换,我们也把它用矩阵形式来表示:
,为了方便公式之间的转换,我们也把它用矩阵形式来表示:![]()
![]() ,其中t为
,其中t为![]() 。总结一下,K为相机内参,是一个固有属性;R和t都为相机外参,其中R为旋转矩阵,t为平移向量。
。总结一下,K为相机内参,是一个固有属性;R和t都为相机外参,其中R为旋转矩阵,t为平移向量。

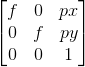
![\begin{bmatrix} f & 0 & px\\ 0 & f& py\\ 0 & 0& 1 \end{bmatrix}\begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0 & 1& 0 \end{bmatrix}=K[I|0]](http://img.e-com-net.com/image/info8/e8051d82027b430f8365fa3584977335.gif)