共轭梯度法

概述

作为一种迭代的优化方法，共轭梯度（Conjugate Gradient，cg）由Hestenes和Stiefe于1951年提出。cg是针对形如式(1-1)的优化方法。

Ax=b(1-1)

需要指出的是，式(1-1)有着广泛的应用场景。例如，令 x∗ 为二次问题（如式(1-2)所示）的最小值：

f(x)=12xTAx−bx(1-2)

x∗=argminxf(x)(1-3)

则有

∇f(x∗)=Ax∗−b=0(1-4)

显然，式(1-4)可以用cg方法求解。
此外，牛顿法的每轮迭代需要计算 dk=−(H(k))−1gk ，即 H(k)dk=−gk 。此时，也可以使用cg来求取。

原理

共轭的定义

令 A∈Rn×n 是对称正定矩阵。对于 d(i),d(j)∈Rn ，若有 (d(i))TAd(j)=0 ，则称 d(i) 与 d(j) 关于 A 共轭。

对于一组向量 d(1),d(2),...,d(k)∈Rn ，若它们两两关于 A 共轭，即 (d(i))TAd(j)=0,i≠j ，则称该组向量关于 A 共轭。

需要指出的是，共轭是正交的推广。这是因为，若 A=I ，则有 (d(i))TId(j)=0⇒d(i)⊥d(j)

可以证明关于 A 共轭的一组向量 d(1),d(2),...,d(k) 线性无关。

几何意义

对于二次函数

f(x)=12(x−x∗)TA(x−x∗)(2-1)

其中 A∈Rn×n 是对称正定矩阵， x0 是某已知点。那么，有

12(x−x∗)TA(x−x∗)=c(2-2)

是以 x∗ 为中心的椭球面。如图2-1所示：

图2-1 二次函数#

由于 ∇f(x∗)=A(x∗−x∗)=0 ，且 ∇2f(x∗)=A>0 ，所以 x∗ 是 f(x) 的极小点。

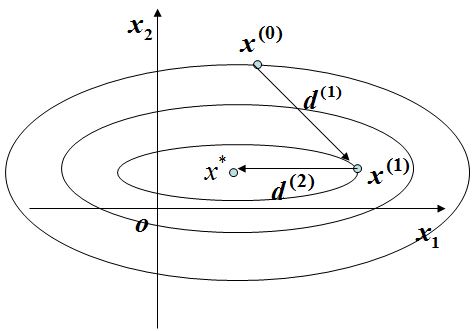
令 x(0) 是某等值面上一点， d(1)∈Rn 是其搜索方向， x(1) 是 x(0) 沿着 d(1) 以最佳步长搜索得到的点，那么 d(1) 是 x(1) 所在等值面的切向量。其对应的法向量为

∇f(x(1))=A(x(1)−x∗)(2-3)

所以 d(1) 与 ∇f(x(1)) 正交。即 d(1)A(x(1)−x∗)=0 。令 d(2)=x(1)−x∗ ，那么 d(1) 与 d(2) 关于A共轭。 也就是说，等值面上某点的切向量与该点指向极小点的向量关于A共轭。如图2-2所示：

图2-2 共轭方向#

共轭方向

对于

f(x)=12xTAx+bTx+c(2-4)

其中 A∈Rn×n 是对称正定矩阵。 d(1) , d(2) ,…, d(k) 是一组关于A的共轭向量。那么从任意 x(1) 开始，依次沿 d(1) , d(2) ,…, d(k) 搜索，设得到的点依次为 x(2) , x(3) ,…, x(k+1) 。那么 x(k+1) 是 f(x) 在 x(1)+Bk 上得到的极小点，其中

Bk={x|x=∑i=1kλid(i)}(2-5)

特别的，当 k=n 时， x(n+1) 是 f(x) 在 Rn 上的唯一极小点。

因此，对于式(2-4)，可以按照如下步骤求解最小值
1. 取定一组关于A的共轭方向 d(1) , d(2) ,…, d(k)
2. 任取点 x(1) ，依次按照如下过程由 x(k) 确定 x(k+1)

{x(k+1)=x(k)+λkd(k)f(x(k)+λkd(k))=minλf(x(k)+λkd(k))(2-6)

直至某个 x(k) 满足 ∇f(x(k))=0

共轭梯度

将共轭方向的思想与最速下降法（steep descent）相结合，利用已知迭代点处的梯度构造一组共轭方向，并按此方向进行搜索，求出函数的极小值。

实现

对于式(1-1)按照如下步骤求解

1. 初始化
   选取初始点 x(0) ，令第一个搜索方向为
   
   d(0)=−r(0)=Ax(0)−b(3-1)
   其中， r(⋅) 称为当前解 x(⋅) 关于式(1-1)的残差
2. 求解当前搜索方向
   设当前迭代点为 x(k) ，则 r(k)=Ax(k)−b ，则下一个搜索方向按如下方式计算
   
   d(k)=−r(k)+β(k−1)d(k−1)(3-2)
   由于要求 d(k−1) 和 d(k) 关于 A 共轭，因此
   
   0=(d(k−1))TAd(k)=(d(k−1))TA(−r(k)+β(k−1)d(k−1))(3-3)
   
   可以计算出
   
   β(k−1)=(d(k−1))TAr(k)(d(k−1))TAd(k−1)=(r(k))TAd(k−1)(d(k−1))TAd(k−1)(3-4)
3. 求解当前步长
   x(k+1)=x(k)+α(k)d(k)
   根据line search的方法，可以求解得到
   
   α(k)=(d(k))TAr(k)(d(k))TAd(k)
   
   4 更新残差
   
   r(k+1)=r(k)+α(k)Ad(k)
4. 循环2,3,4步，直至满足终止条件

根据Krylov子空间的一些性质，可以将的迭代过程简化为：

α(k)=(r(k))Tr(k)(d(k))TAd(k)=||r(k)||2(d(k))TAd(k)

β(k)=(r(k+1))Tr(k+1)(r(k))Tr(k)=||r(k+1)||2||r(k)||2

精简上述分析，得到如下的共轭梯度算法
x(0)=0 , r(0)=b ,
for k=0,1,2.⋯
1. if ||r(k)||≤ϵ||b|| , return x(k)
2. if k=0 , d(k+1)=r(k) ; else， d(k+1)=r(k)+β(k)d(k)
2. α(k+1)=||r(k)||2(d(k+1))TAd(k+1)
3. x(k+1)=x(k)+α(k+1)d(k+1)
4. r(k+1)=r(k)−α(k+1)Ad(k+1)
5. β(k+1)=||r(k+1)||2||r(k)||2