线性代数的本质
参考3Blue1Brown中的视频
1. 向量究竟是什么
物理角度：
，空间中的箭头，包含长度和方向；处于平面中的向量是二维的，处于空间中的向量是三维的
计算机角度：
，有序的数字列表
数学角度：
，向量可以是任何东西，只要加法和数乘有意义即可
多种角度之间的联系：首先从物理角度理解向量；然后从计算机角度用数字列表表示向量（第一个数表示沿x轴走多远，第二个数表示沿y轴走多远，第三个数表示沿z轴走多远，以此类推）；
向量和点的区别：向量的惯用做法是把数字竖着写，然后用方括号包起来，点的惯用做法是把数字横着写，然后用圆括号包起来
向量的两种基本运算：加法和数乘。加法是线性代数中唯一允许向量离开原点的情形，可以把向量看作一种特定的运动，计算机角度，加法就是对应项相加；数乘就是缩放向量。同时，一个向量又可以看成两种基本运算的结合（缩放向量并且相加）：
2. 线性组合，张成的空间，基
基：任何一个向量，都可以看成基向量的数乘和
线性组合：两个向量数乘之和的结果，被称为两个向量的线性组合
线性空间：全部线性组合构成的向量集合，称为“张成的空间”
向量与点：用向量的终点代表某向量
线性相关：一组向量中，至少有一个是多余的，没有对张成空间做出任何贡献，移除其中一个也不会减小张成的空间，当这种情况发生时，称这组向量“线性相关”
线性无关：如果所有向量都给张成的空间增加了新的维度，就称这组向量“线性无关”
空间的基：张成该空间的一个线性无关的向量集合
3. 矩阵，线性变换
线性变换：
“变换”本质上是“函数”的一种花哨叫法，它接收输入内容，并输出对应内容，在线性代数中，它接收一个向量，并输出一个向量，即向量的函数，使用“变换”暗示要用“运动”来思考。
“线性”：1. 直线变换后仍然是直线，不能有所弯曲 2. 原点必须保持固定。变换可以非常复杂，线性代数仅研究一种特殊的容易理解的变换，即“线性变换”，保持网格线平行并等距分布的变换
matlab相关代码
如何用数值描述线性变换？线性空间的变换其实就是矩阵向量乘法（数乘之和），只需要记录基向量变换后的位置即可：
变换后的基向量构成了变换矩阵。二维线性变换由4个数字确定，即i变换后的两个坐标和j变换后的两个坐标，将这些坐标包装在一个2x2的格子里，称为变换矩阵；三维线性变换由9个数字确定。
矩阵：矩阵只是一个记号，用来描述线性空间变换的信息，矩阵的列，就是变换后的基向量
线性变换是操纵空间的一种手段，看到矩阵，就把它解读为对空间的一种变换
4. 线性变换复合
复合变换：一个变换之后再进行另一个变换，总体来说，是一个新变换，即前两个独立变换的复合变换，不过需要注意，乘积需要从右向左读，类似于函数 f(g(x))
二维空间中的概念，可以完美地推广到多维空间
5. 行列式
行列式：测量线性变换究竟对空间有多少拉伸或挤压，即变换前后的面积或体积缩放比例。行列式为0，说明线性变换将整个平面压缩到一条线，甚至是一个点，即将空间压缩到更小的维度
6. 逆矩阵，列空间，秩，零空间
线性代数被广泛应用的一个原因是，它可以求解特定的方程组-线性方程组，它和矩阵向量乘法非常相似
逆矩阵：逆向变换的矩阵，称为逆矩阵
列空间(column space)：变换矩阵的列向量张成的空间，变换后的基向量张成的空间
秩(rank)：列空间的维数，秩最多与列数相等（满秩）
零空间(null space)：变换后落在原点的向量集合，被称为矩阵的零空间或核
不同维数之间的变换是完全合理的，比如一个将二维向量变为三维向量的变换
7. 点积
点积：只有通过线性变换，才能真正理解点积--将左边的向量转化为矩阵，该矩阵表示的信息为多维空间到一维空间（数轴）的线性变换，该变换将向量转化为数
对偶性：两种数学事物之间自然而又出乎意料的对应关系，例如，向量的对偶是它定义的（多维空间到一维空间的）线性变换，多维空间到一维空间的线性变换的对偶是多维空间中的某个特定向量
点积是理解投影的有效几何工具，方便验证两个向量的指向是否相同
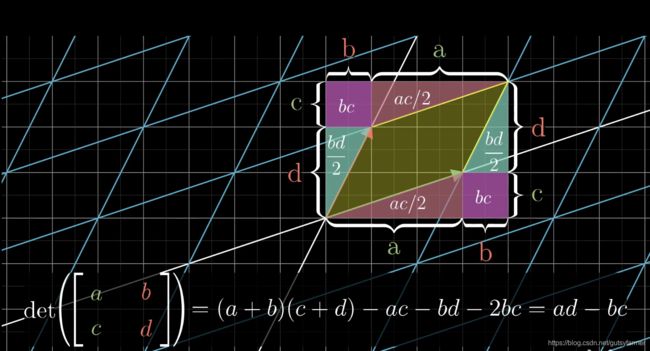
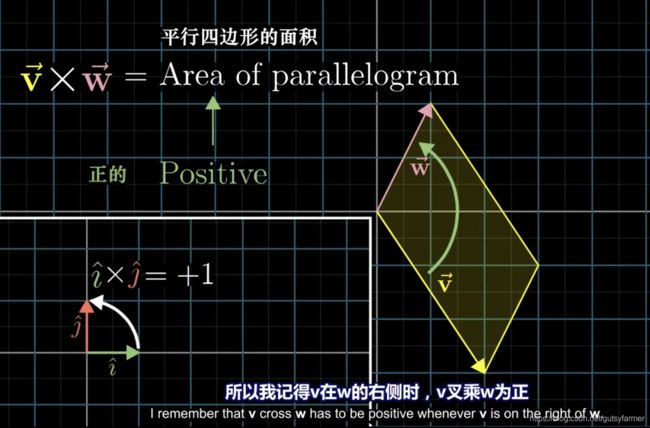
8. 叉积
叉积：平行四边形的面积
二维向量的叉积：两个向量组成的矩阵的行列式即为叉积
三维向量的叉积：两个三维向量，生成一个三维向量，向量的长度为平行四边形的面积，方向与平行四边形（所在的面）垂直
理想的情况是绘出一幅美景，让证明显而易见
9. 基变换
坐标系：发生在向量与一组数之间的任意一种转化，都被称为一个坐标系，每个坐标系都有自己的基向量
使用不同基向量的思想：不同的坐标，但实际上表示的是空间中的同一个向量，只是视角不同而已。为什么要进行坐标系变换？
不同坐标系之间的转化：
非标准基下，逆时针旋转90°的变换矩阵：
10. 特征向量和特征值
eigenvector：在变换中停留在它张成的空间里的向量，称为特征向量，非特征向量变换后会发生旋转
eigenvalue：在变换后特征向量的缩放比例
eigenbasis：特征向量作为基向量，特征基不一定是对角矩阵
对角矩阵：可以解析为--所有基向量都是特征向量，对角元是它们所属的特征值（基向量与特征值相乘）；对角矩阵在很多方面都更容易处理
如果一个变换有许多特征向量，且足够幸运，能够张成全空间，那么你就可以变换坐标系，用特征向量作为基向量，E^{-1}AE为同一个变换，不过是从新基向量构成的坐标系的角度来看的。用特征向量来完成这件事的意义在于，E^-1AE 为对角矩阵，对角元为特征值，对角矩阵的幂计算很简单。但并不是所有变换(矩阵)都能进行对角化，例如剪切变换，它的特征向量不够多，不能张成全空间。
不过，二维线性变换不一定有特征向量，例如90°的旋转变换；且会出现一个特征向量，但特征值不在一条直线上的情况，例如将所有向量变为两倍的矩阵；