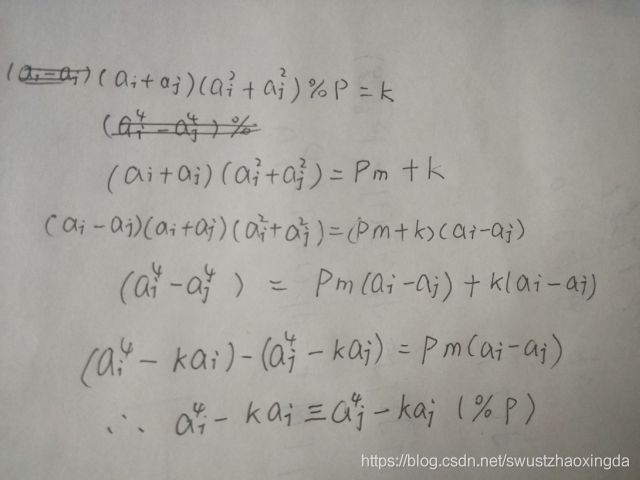Count Pairs CodeForces - 1188B 推式子

You are given a prime number pp , nn integers a1,a2,…,ana1,a2,…,an , and an integer kk .

Find the number of pairs of indexes (i,j)(i,j) (1≤i

Input

The first line contains integers n,p,kn,p,k (2≤n≤3⋅1052≤n≤3⋅105 , 2≤p≤1092≤p≤109 , 0≤k≤p−10≤k≤p−1 ). pp is guaranteed to be prime.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai≤p−10≤ai≤p−1 ). It is guaranteed that all elements are different.

Output

Output a single integer — answer to the problem.

Examples

Input

3 3 0
0 1 2

Output

1

Input

6 7 2
1 2 3 4 5 6

Output

3

Note

In the first example:

(0+1)(02+12)=1≡1mod3(0+1)(02+12)=1≡1mod3 .

(0+2)(02+22)=8≡2mod3(0+2)(02+22)=8≡2mod3 .

(1+2)(12+22)=15≡0mod3(1+2)(12+22)=15≡0mod3 .

So only 11 pair satisfies the condition.

In the second example, there are 33 such pairs: (1,5)(1,5) , (2,3)(2,3) , (4,6)(4,6) .

、震惊，居然是道大水题

#include
using namespace std;
typedef long long ll;
const int maxn=3e5+15;
ll a[maxn];
mapmp;
int main()
{
    ll n,p,k;
    cin>>n>>p>>k;
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]);
    for(int i=1;i<=n;i++)
    {
        long long tp1=(a[i]*a[i]%p*a[i]%p*a[i]%p-k*a[i]%p+p)%p;
        mp[tp1]++;
    }
    long long ans=0;
    for(auto it=mp.begin();it!=mp.end();it++)
    {
        ans+=(it->second)*((it->second)-1)/2;
    }
    cout<