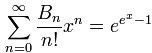集合划分问题（贝尔数）

集合划分问题

Time Limit:1000MS    Memory Limit:32768KB    64bit IO Format:%I64d & %I64u

Submit Status

Description

n个元素的集合{1,2,...,n}可以划分若干个非空子集。例如，当n=4时，集合{1,2,3,4}可以划分为15个不同的非空子集如下:

 
{{1},{2},{3},{4}},
{{1,2},{3},{4}},
{{1,3},{2},{4}},
{{1,4},{2},{3}},
{{2,3},{1},{4}},
{{2,4},{1},{3}},
{{3,4},{1},{2}},
{{1,2},{3,4}},
{{1,3},{2,4}},
{{1,4},{2,3}},
{{1,2,3},{4}},
{{1,2,4},{3}},
{{1,3,4},{2}},
{{2,3,4},{1}},
{{1,2,3,4}}

给定正整数n(1<=n<=20),计算出n个元素的集合{1,2,...,n} 可以化为多少个不同的非空子集。

Input

多组输入数据，每组数据1行，表示元素个数n.

Output

对于每组数据，输出一行一个数，表示不同的非空子集的个数。

Sample Input

24

Sample Output

215

解题思路（From Internet）：

设n个元素的集合可以划分为F(n,m)个不同的由m个非空子集组成的集合。

考虑3个元素的集合，可划分为
① 1个子集的集合：{{1，2，3}}
② 2个子集的集合：{{1，2}，{3}}，{{1，3}，{2}}，{{2，3}，{1}}
③ 3个子集的集合：{{1}，{2}，{3}}
∴F(3,1)=1;F(3,2)=3;F(3,3)=1;

如果要求F(4,2)该怎么办呢？

A.往①里添一个元素{4}，得到{{1，2，3}，{4}}

B.往②里的任意一个子集添一个4，得到
{{1，2，4}，{3}}，{{1，2}，{3，4}}，
{{1，3，4}，{2}}，{{1，3}，{2，4}}，
{{2，3，4}，{1}}，{{2，3}，{1，4}}

∴F(4,2)=F(3,1)+2*F(3,2)＝1+2*3＝7

推广，得F(n,m)=F(n-1,m-1)+m*F(n-1,m)

后来发现这就是组合数学里面的贝尔数。

Bell数的定义：第n个Bell数表示集合{1,2,3,...,n}的划分方案数，即：B[0] = 1;

 

 

每一个Bell数都是第二类Stirling数的和，即：

 

 

第二类Stirling数的意义是：S(n,k)表示将n个物体划分成k个非空的不可辨别的（可以理解为盒子没有编号）集合的方法

数。很明显，每一个Bell是对应的第二类Stirling数之和。

 

Bell数的指数生成函数是：

 

注意本题要用long long型。

/*
* Copyright (c) 2016, 烟台大学计算机与控制工程学院
* All rights reserved.
* 文件名称：number.cpp
* 作    者：单昕昕
* 完成日期：2016年4月29日
* 版 本 号：v1.0
*/
#include
#include
#include
#include
#include
using namespace std;
long long S(long long m,long long n)
{
    if(m==1)
        return 1;
    if(m==n)
        return 1;
    else
        return S(m-1,n-1)+S(m,n-1)*m;
}

int main()
{
    long long n,i;
    while(cin>>n)
    {
        long long sum=0;
        for(i=1; i<=n; i++)
            sum+=S(i,n);
        cout<