双平衡三进制计算细节
很久以前罗列过一些关于"双平衡三进制"的内容, 都挺短的, 而且有点过时,
https://segmentfault.com/a/11...
最近在 Nim 里边实现了一个版本, 顺着整理了一下.
https://github.com/dual-balan...
平面的表示
双平衡三进制是我大学时候发现的一个比较有意思的平面表示方式,
中学数学, 我们用笛卡尔坐标系来表示平面的, 而且图形界面也常用这个方法,
但是笛卡尔坐标系表示平面用的是两个数字, 就没有那么直观了.
基于一维的线段上十进制表达点位置的方式, 我推想怎样表示平面更直观...
首先一维的表示位置的方式, 先有一个单位长度 1, 超出长度放大 10 倍, 直到包含目标位置,
然后要精确定位的话, 就是十等分再十等分, 直到无限接近目标位置.
在平面上, 单位元一般就是一个正方形, 那么仿照一维的方式,
如果目标位置在外部, 就不断倍数放大正方形, 然后等分正方形, 直到无限接近目标位置.
这样做, 有个绕不过去的问题, 就是单位放大的时候, 默认是朝着一个方向放大的,
1, 10, 100... 然后反方向就需要负数表示了, 在二维空间也是一样,
我就想能不能直接用更简洁的方式表示呢, 后来想到把正方形按照九宫格放大,
那么, 原来的的单位正方向, 就处在大的区域中间, 这样也是满足要求的,
而等分的时候, 单位正方形中心点, 依然是中间的正方形的中心点,
这样在思路上是行得通的, 也相对比较直观, 也就是数独的样子
后来仔细了解的时候, 我了解到对于一维来说, 已经有个"平衡三进制"的表示法
https://zh.wikipedia.org/wiki...
这个就跟我用九宫格表示平面的思路一致了, 零点在中心, 左右两边各一个单位长度.
于是我这边的命名也就跟着同步, 叫做"双-平衡三进制"了.
(写文章的时候搜到个图示, 这个很好展示了"三进制"和"平衡三进制"的区别.)
符号定义
后面为了简化表示, 我考虑定义一下符号, 刚开始想过箭头什么的,
不过因为电脑不方便输入, 而且也很奇怪, 没深入.
我注意到是九宫格, 就把三阶幻方的数字引过来试试了,
三阶幻方古代有个名字叫"洛书", 我也拿过来当项目代号了, 长这样:
4 9 2
3 5 7
8 1 6幻方基本的数学性质就是平衡, 行列斜向各自相加分别都是 15.
我后来表示的时候, 为了直观的方便, 把 1 定为前方, 所以就倒转了一下,
大致想想, 1 放在北方, 我们现在的人看看是更习惯一点, 而且后面计算也方便.
6 1 8
7 5 3
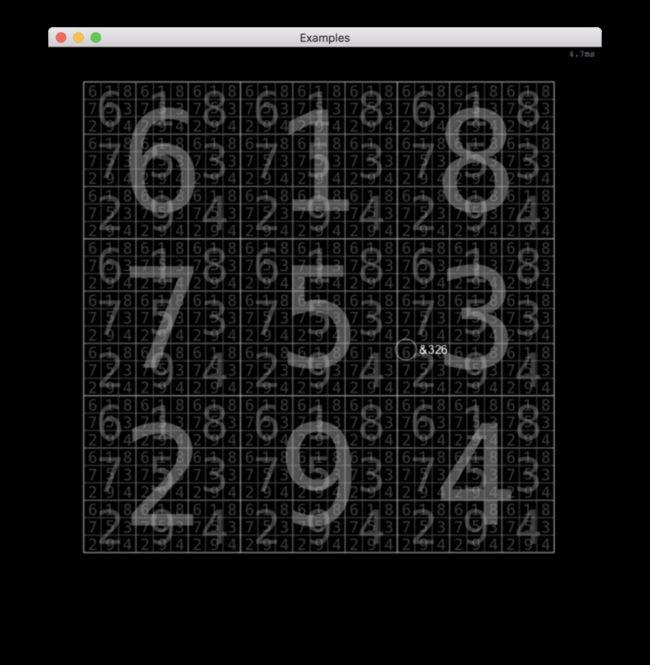
2 9 4基于这样的方式, 就可以用来表示一个平面上的各个位置了.
比如 &326, 前面用 & 标记是一个"双平衡三进制数",
在这个区域里边, &326 第一位 3 定位了右边一个大的区域,
然后第二位 2 定位了左下角位置, 再然后 6 定位右上角位置,
这样就比较直观表示了一个区域了, 如果用笛卡尔坐标系就是 (5, -2).
这样一对比, 也可以看到所谓的"直观"其实只是某个方面上的直观,&326 我知道 &3??第一位的时候, 就能知道一个大致的区域了,
然后再是 &32?, 一步步更加精确到 9 个格子当中的一个.
从简短来说, (5, -2) 已经非常简短了. 换一种表达, 反而边长了.
因为这样的对应关系, 所以笛卡尔坐标表示的区域, 也就能用双平衡三进制表示.
至于实际上是不是有好处, 这也就比较飘忽了.
数值计算
现在我用 Nim 实现的模块当中包含加减乘除这四个运算,
中间包含反转和旋转, 不过相对来说不那么实用了.
基于上面那个图, 可以看到比较直接的加法的一些规则:
&5 + &5 = &5 # 这个是原点了
&5 + &1 = &1 # 原点加上任何 x 都得到 x
&3 + &7 = &5 # 两个相反的数想相加, 得到原点
&4 + &6 = &5 # 同上
&1 + &7 = &6 # 左 + 上 = 左上然后还有包含进位的情况:
&1 + &1 = &19 # 进位了, &19 相当于 3 + (-1)
&4 + &4 = &46 # 右下角
&8 + &1 = &14 # 对照图形了...参照图形上的样子, 这个还是比较容易看出来的.
对于减法, 也就是先对数值去反, 然后再相加. 比较简单了.
然后是乘法,
&1 * &1 = &1 # 这时候 &1 是不动点, 单位元
&1 * &7 = &7 # 单位元乘以任何数 x 都得到 x
&9 * &9 = &1 # 相当于 (-1) * (-1)
&3 * &3 = &9 # 对照图形, 相当于旋转
&7 * &7 = &9
&4 * &4 = &73 # 注意旋转加上进位复杂的我不罗列了. 但是中间有个比较有意思的规律,
就是奇数奇数相乘的时候, 偏偏跟十进制乘法的尾数对上的,
比如说 3 * 7 = 21, 这边也有 &3 * &7 = &1, 以及三三得九.
感觉不是巧合, 但是我也没仔细挖掘出来, 验证了一下都是满足的.&3 * &4 = &2, &4 * &9 = &6, 都是的.
进位方面跟十进制或者二进制都是一样玩的, 不深入说了.
除法
除法实现起来是比较头疼的, 虽然也可以参考十进制二进制的思路,
不过中间实现会遇到一个问题, 就是某些情况会不够准确.
十进制除法, 因为是不平衡的, 大小区分就很容易, 大于就大于了.
然而表示平面的时候, 就没有那么直观的大于, 因为会有多个方向的.
比如图上看 &199 &511 的位置, 就是挨着的, 但是首位数字差挺多的,
这就导致列竖式进行计算的时候, 有些情况取值会不准确,
特别是写程序的时候, 总不能计算的时候再强行算一下偏差大小作对比吧.
后来经过比较多的思考, 我尝试参考复数的计算, 分开坐标轴计算,
a + b*i (a + b*i) * (c - d*i)
-------- = ---------------------
c + d*i (c + d*i) * (c - d*i)
(a * c - b * d) + (b * c - a * d)*i
= -----------------------------------
c * c + d * d
(a * c - b * d) (b * c - a * d)*i
= --------------- + ------------------
c * c + d * d c * c + d * d其中 c * c + d * d 在复数计算当中已经知道, 只有一个方向的分量的值.
在 x 方向上, 只有 &3 &7 的值, y 方向只有 &1 &9,
这样就能进行转化沿用复数的方案了, 加减法和乘法都是有的.
然后我就只需要搞定 &1 &5 &9 构成的平衡三进制除法就好了.
这个步骤还是比较绕的. 我想了想还是担心平衡三进制除法有问题, 最后实现出来效果还行.
具体涉及到代码, 我也不再展开了, 思路就是这个思路了.
https://github.com/dual-balan...
其他
从前面的描述也就能看到, 双平衡三进制的思路有点不一样,
十进制我们的习惯是一个点对应一个位置, 包括二进制三进制也是,
但是双平衡三进制, 比如 &1, 虽然也是一个点, 同事也像是代表一个区域.
具体从计算来说, 还是一个点, 否则没法有准确的值了.
习惯上十进制的数, 分数的时候, 我们有 0.5 表示一半, 0.33333... 表示 3/1,
这里拜三进制所赐, 1/2 是一个无法整除的数, 可以是 &1.11111... 或者 &19.99999....
可以看到边界上的一个点是可以从两个方向逼近的, 或者也可以是 4 个方向,
比如 &8.888... &82.222... &14.444... 36.666... 都逼近同一个点.
目前综合看下来, 这个方案就是比较有意思, 但是说不上能有什么好处,
另外看到 WIKI 上还有平衡三进制的开分计算, 就复杂了, 没有尝试过.