离散数学——朴素集合论

一、集合
  集合是不同对象的一个无序的聚集，对象称为集合的元素。

1.1 集合的概念
  描述集合的方法有多种方式。一种方式是在可能的情况下一一列出集合中的元素，称为枚举，如$$A=\{1,2,3,4\}$$另一种方法是集合构造器，形如$$B=\{x|P(x)\}$$描述了满足$P$的元素。当集合不包含任何元素，称为空集，记作$\varnothing$。
  设$A,B$为集合，若$A$中的每个元素都属于$B$，则称$A$是$B$的子集，记作$$A\subseteq B$$如果有$A\subseteq B,B\subseteq A$，那么称$A$与$B$相等，记作$$A=B$$  ;设$A$为集合，称$A$的所有子集形成的集族称为$A$的幂集，记作$2^A$。

1.2 集合的运算
  两个或多个集合可以以许多不同的方式结合在一起。
  令$A$和$B$为集合，集合$A$和$B$的并运算描述了包含属于$A$或$B$的一切元素，其形式为$$A\cup B=\{x|x\in A\vee x\in B\}$$  令$A$和$B$为集合，集合$A$和$B$的交运算描述了包含同时在$A$或$B$的元素，其形式为$$A\cap B=\{x|x\in A\wedge x\in B\}$$  对于交与并运算，满足分配律$$\begin{gathered} A\cap (\bigcup _{i\in I}{A}_i)=\bigcup _{i\in I}(A\cap A_i) \\ A\cup (\bigcap _{i\in I}{A}_i)=\bigcap _{i\in I}(A\cup A_i) \end{gathered}$$考察分配律的正确性，设$x\in A\cup ({\bigcap }_{i\in I}{A}_i)$，那么有$$x\in A\vee x\in \bigcap _{i\in I}{A}_i$$故$$x\in A\vee \forall i\in I,x\in A_i$$即$$\forall i\in I,x\in A\vee x\in A_i$$亦即$$\forall i\in I,x\in A\cup A_i$$于是$$x\in \bigcap _{i\in I}(A\cup A_i)$$故对于任意的$x\in A\cup ({\bigcap }_{i\in I}{A}_i)$，有$x\in {\bigcap }_{i\in I}(A\cup A_i)$。故$$A\cup (\bigcap _{i\in I}{A}_i)\subseteq \bigcap _{i\in I}(A\cup A_i)$$同理可证$$\bigcap _{i\in I}(A\cup A_i)\subseteq A\cup (\bigcap _{i\in I}{A}_i)$$故$$A\cup (\bigcap _{i\in I}{A}_i)=\bigcap _{i\in I}(A\cup A_i)$$在简单情况下，上述公式可以一般化为$$\begin{gathered} A\cap (B\cup C)=(A\cap B)\cup (A\cap C) \\ A\cup (B\cap C)=(A\cup B)\cap (A\cup C) \end{gathered}$$  令$A$和$B$为集合，集合$A$和$B$的差运算描述了属于$A$但不属于$B$的元素，其形式为$$A-B=\{x|x\in A,x\notin B\}$$交、并、差运算满足分配律。但差运算是不对称的，还有一种差运算是对称差，令$A$和$B$为集合，对称差描述了不同时属于两个集合的元素，记作$$A\Delta B=(A-B)\cup (B-A)$$
1.3 集合的补集
  令$A$与$S$为集合，且$A\subseteq S$，定义$A$在$S$上的补集$$A^c=\{x|x\in S,x\notin A\}$$补集具有两条特征性质：$$\begin{gathered} A\cup A^c=S \\ A\cap A^c=\varnothing \end{gathered}$$且$$\begin{gathered} (\bigcup _{i\in I}{A}_i{)}^c=\bigcap _{i\in I}{A}_i^c \\ (\bigcap _{i\in I}{A}_i{)}^c=\bigcup _{i\in I}{A}_i^c \end{gathered}$$称为德摩根【De Morgan】定律。

1.4 笛卡尔积
  设$S$是一个集合，且有元素$x,y\in S$，那么有序二元组$(x,y)$称为序对。设集合$A,B\subseteq S$，则$$A\times B=\{(x,y)|x\in A\wedge y\in B\}$$称为$A$与$B$的笛卡尔积，笛卡尔积是不封闭的。
  集合$A_1,A_2,...A_n$的笛卡尔积用$$A_1\times A_2\times ...\times A_n$$表示，是有序元组$(a_1,...,a_n)$的集合，且要注意的是，$(A\times B)\times C$不等同于$A\times B\times C$，并使用$A^n$来表示集合$A$自身的笛卡尔积。
  考虑集合$\Sigma$，其元素是ASCII码的所有字符，并抽象的认为${\Sigma }^0$是计算机的空格键。那么考虑$${\Sigma }^{\ast }={\Sigma }^0\cup \Sigma \cup {\Sigma }^2\cup ...\cup {\Sigma }^n\cup ...$$那么可以认为${\Sigma }^{\ast }$是自然语言的所有集合的数学模型，这是笛卡尔积描述事物的抽象方法。

1.5 集合的基数
  令$S$为集合，如果$S$中恰有n个不同的元素，其中n是非负整数，就称$S$是有穷集合，而称n是$S$的基数，记作$$|S|=n$$且对于集合$A$与$B$有如下计数法则：
  -$A\cap B=\varnothing$，则$|A\cup B|=|A|+|B|$；
  -$|A\times B|=|A|\times |B|$。
多个集合的计数法则称为容斥原理，形如
$$\begin{array}{rl}|\bigcup _{i=1}^n{A}_i|=& |A_1|+|A_2|+...\\ & -|A_1\cup A_2|-...\\ & -...\\ & -|A_1\cup A_2\cup ...\cup A_n|\end{array}$$

---

二、映射
  在许多情况下，都会为一个集合的元素指派另一个集合中的某一个特定的元素。例如离散数学课程的每个学生都会指派一个得分，这就是函数的一个例子，函数也被称为映射。

2.1 映射的概念
  令$A$和$B$为非空集合。从$A$到$B$的函数$f$是对元素的一种指派，对$A$的每个元素恰好指派$B$的一个元素。如果$B$中元素$b$是唯一由函数$f$指派$a$的，则记作$f(x)=y$；如果$f$是从$A$到$B$的函数，则记作$f:A\to B$。
  若有映射$I_x:X\to X,\forall x\in X,I_x(x)=x$，则称该映射为恒等映射。
  设$f,g:X\to Y,\forall x\in X,f(x)=g(x)$，则称映射$f$与$g$相等。
  令$f$是从$A$到$B$的映射，若对于$f$定义域内的所有$x$与$y$，都有$f(x)=f(y)$蕴含$x=y$，则称映射是单射的；若对于每个$y\in B$都有$x\in A$使得$f(x)=y$，则称映射是满射的或映上的；若映射既是单射的，又是映上的，则称该映射是双射的。

2.2 鸽巢原理
  有20只鸽子要飞往19个鸽巢栖息。由于有20只鸽子，而只有19个鸽巢，所以这19个鸽巢中至少有1个鸽子里最少栖息着2只鸽子。如果每个鸽巢中最多栖息1只鸽子，那么最多只有19只鸽子有住处，其中每只鸽子一个巢。这个例子阐述了一个一般原理，叫做鸽巢原理，该原理断言：如果鸽子数比鸽巢数多，那么一定有一个鸽巢里至少有2只鸽子。
  当然，这个原理除了鸽子和鸽巢外也可以用于其他对象。一般地，如果k+1或更多的对象放入k个集合中，那么至少有一个集合包含2个或更多的对象。鸽巢定理也称为迪利克雷抽屉原理，其可以推断：一个从有k+1或更多个元素的集合到k个元素的集合的函数$f$不是一对一函数。
  考虑从集合$\{1,2,...,2n\}$中取n+1个数$a_1,...,a_{n+1}$，则$\exists 1\le i,j\le n+1$，使得$a_i|a_j$或$a_j|a_i$。因为考虑可以令$a_i=2^{s_i}\cdot d_i$，其中$d_i$为奇数，那么集合中有n个奇数，选择$n+1$个数必然使得存在$a_i$与$a_j$，有$d_i=d_j$，即$a_i|a_j$或$a_j|a_i$。

2.3 映射的性质
  对于映射$f:X\to Y$，取$A\subseteq X,B\subseteq Y$，则有集合$A$的元素通过$f$映射成元素的集合，记为$$f(A)=\{f(x)|x\in A\}$$称为$A$在$f$下的象；同理，$f^{-1}(B)$称为$B$在$f$下的原象。
  考虑映射$f:X\to Y$，取$A,B\subseteq Y$，取$x\in f^{-1}(A\cap B)$，则$$f(x)\in A\cap B$$那么$$f(x)\in A,f(x)\in B$$因此$$x\in f^{-1}(A),x\in f^{-1}(B)$$即$$x\in f^{-1}(A)\cap f^{-1}(B)$$反之，对于$x\in f^{-1}(A)\cap f^{-1}(B)$亦有$x\in f^{-1}(A\cap B)$。因此$$f^{-1}(A\cap B)=f^{-1}(A)\cap f^{-1}(B)$$同理，有$$\begin{gathered} f^{-1}(A\cup B)=f^{-1}(A)\cup f^{-1}(B) \\ {f}^{-1}(A^C)=f^{-1}(A{)}^C \\ {f}^{-1}(A-B)=f^{-1}(A)-f^{-1}(B) \\ {f}^{-1}(A\Delta B)=f^{-1}(A)\Delta f^{-1}(B) \end{gathered}$$而对于映射$f:X\to Y$，取$A,B\subseteq X$，取$y\in f(A\cap B)$，则有性质$$\begin{gathered} f(A\cap B)\subseteq f(A)\cap f(B) \\ f(A\cup B)=f(A)\cup f(B) \end{gathered}$$

2.4 映射的合成
  令映射$f:X\to Y,g:Y\to Z$，则映射$f$与$g$的合成定义为$h:X\to Z$，即$h(x)=g(f(x))$，记作$h(x)=(g\circ f)(x)$。
  设$f:X\to Y,g:Y\to Z,h:Z\to W$，则有$$h\circ g\circ f=(h\circ g)\circ f$$但映射的合成不满足交换律。
  设$f:X\to Y,I_x:X\to X,I_y:Y\to Y$，那么有$$f\circ I_x=f=I_y\circ f$$ 
  令$f$是从$A$到$B$的双射映射，那么对于$f(x)=y$，$f$的逆映射形如$f^{-1}$且有$f^{-1}(y)=x$。映射$f$存在逆映射的充要条件为映射$f$是双射的。
  令$f$是从$A$到$B$的双射映射，$g$与$h$均是$f$的逆映射，则有$g=h$，称为逆映射的唯一性。
  若对于$f:X\to Y,g:Y\to X$，使得$g\circ f=I_x,f\circ g=I_y$，那么$f$与$g$互为逆映射。
  设$f:X\to Y$，若$\exists g:Y\to X$，使得$g\circ f=I_x$，则称$f$是左可逆映射，且$f$是单射的；反之，若$f$是右可逆的，则$f$是上映的。

2.5 映射的置换
  取集合$S,|S|<\infty$，取映射$\sigma :S\to S$，若$\sigma$是双射的，则$\sigma$是$S$的一个置换。典型的，对于集合$\{1,2,...,n\}$，取$S_n=\{\sigma |\sigma :S\to S\}$，那么显然，$S_n$是一个序列的全排列，对第i个元素的置换记为$i\sigma$。
  设置换$\sigma :S\to S,\tau :S\to S$，那么定义置换的乘积为$\sigma \cdot \tau$，那么对第i个元素的置换记为$i\sigma \tau$。
  设置换$\sigma :S\to S$，若存在$i_1{\sigma }^k=i_2{\sigma }^{k-1}=...=i_k\sigma =i_1$，且$i_l\sigma =i_l,\forall l\notin \{1,2,...,k\}$则称$\sigma$为k-循环置换，记作$(i_1{i}_2...i_k)$。任一n阶置换均可分解成若干个循环置换。
  当$k=2$时，称为对换。对换具有自反性，即$(ij)=(ij{)}^{-1}$。任一循环置换都可以分解成若干个对换，即任何n阶置换可分解成若干个对换。由于对换的自反性，置换的分解不唯一，但分解的奇偶性不变。考虑置换$\sigma :S\to S$，其被不唯一的分解为$\sigma ={\prod }_{i=1}^s{\sigma }_i={\prod }_{j=1}^t{\tau }_j$，以及取范德蒙行列式$$D=\left|\begin{array}{cccc}1& 1& ...& 1\\ x_1& x_2& ...& x_n\\ ...& ...& ...& ...\\ x_1^{n-1}& x_2^{n-1}& ...& x_n^{n-1}\end{array}\right|$$那么有$D\sigma =(-1{)}^{s}D=(-1{)}^{t}D$，即$s$与$t$的奇偶性一致。
  设$A$为奇置换的集合，$B$为偶置换的集合，那么有$A\cup B=S_n$，$A\cap B=\varnothing$。$\forall a\in A$，那么$aA=\{a\tau |\tau \in A\}$是偶置换，有$aA\subseteq B$，即$|A|=|aA|\le |B|$；反之，$|B|=|bB|\le |A|$，即$|A|=|B|$，即在一个置换中，$|S_n|=n!,|A|=|B|=n!/2$。

2.6 映射与代数
  设$X,Y,Z$是集合，取映射$f:X\times Y\to Z$，称$f$是$X$与$Y$到$Z$的二元运算。
  取集合$X$与运算$\circ :X\times X\to X$以及运算$\ast$，对于$\forall x,y,z\in X$，有如下运算律：
  -若$x\circ y=y\circ x$，称运算满足交换律；
  -若$(x\circ y)\circ z=x\circ (y\circ z)$，称运算满足结合律；
  -若$x\ast (y\circ z)=(x\ast y)\circ (x\ast z)$，称$\ast$运算对$\circ$运算满足左分配律；
  -若$(y\circ z)\ast x=(y\ast x)\circ (z\ast x)$，称$\ast$运算对$\circ$运算满足右分配律。
取集合$X$与运算$\circ :X\times X\to X$，$(X,\circ )$使得离散的集合结构成为代数系统。
  设$X$是集合，$A\subseteq X$，取映射$\chi :X\to \{0,1\}$，且$\forall x\in X$，有$$\chi (x)=\{\begin{array}{rlrl}& 1,& & x\in A\\ & 0,& & x\notin A\end{array}$$则称$\chi$是$A$的特征函数，记作${\chi }_A$。
  考虑$X$的所有子集的集合$\mathrm{X}$，以及集合运算构成的代数系统$(\mathrm{X},\cap ,\cup ,{}^c)$；再考虑$X$的所有子集的特征函数的集合$Ch(x)=\{\chi |\chi :X\to \{0,1\}\}$，以及布尔代数运算构成的代数系统$(Ch,\wedge ,\vee ,\neg )$，这两种系统分别给出了现实问题的抽象形式与计算机系统的抽象形式，且$Ch$与$\mathrm{X}$实质上是双射的。

---

三、关系
  两个集合的元素之间的关系可以表示成一种结构，这种结构称为关系。计算机科学中常常出现的关系，包括程序与其所使用的变量、一种计算机语言与其有效语句之间的关系等。

3.1 二元关系
  设$X$与$Y$是集合，$R\subseteq X\times Y$，那么称$R$是一个$X$与$Y$之间的二元关系。分别取$X$与$Y$的元素$x,y$，若有$(x,y)\in R$，称为$x$与$y$有关系$R$，记作$xRy$。典型的，$N$上的比较运算结果即是一种关系。 $xRy$的结果只能为0或1。
  设$A_1,A_2,...A_n$是集合，$R\subseteq A_1\times A_2\times ...\times A_n$，$R$是一个$A_1,A_2,...A_n$上的n元关系，$A_1,A_2,...A_n$称为关系的域，n称为关系的阶。
  设$X,Y$是集合，二元关系有如下特殊关系：
  -设$I=\{(x,x)|x\in X\}$，称关系$I$为恒等关系；
  -设$R\subseteq X\times X$，$\forall x\in X$，$xRx$，称$R$为自反关系；
  -设$R\subseteq X\times X$，$\forall x\in X$，$xRx$，称$R$为反自反关系；
  -设$R\subseteq X\times Y$，$\forall x\in X,y\in Y$，若$xRy$，都有$yRx$，称$R$是对称关系；
  -设$R\subseteq X\times Y$，$\forall x\in X,y\in Y$，若$xRy$，都有$yRx$，称$R$是反对称关系；
  -设$R\subseteq X\times X$，$\forall x,y\in X$，$xRy$，$yRz$，都有$xRz$，称$R$是传递关系；
  -设$R\subseteq X\times Y$，那么关系的逆记为$R^{-1}=\{(y,x)|(x,y)\in R\}$。
  设$X$与$Y$是集合，$R,S\subseteq X\times Y$，称$R\cap S$，$R\cup S$，$R-S$为关系的交、并、差运算，统称为关系的集合运算。
  设$X,Y,Z$是集合，$R\subseteq X\times Y$，$S\subseteq Y\times Z$，称$R\circ S=\{(x,z)|\exists y\in Y,(x,y)\in R,(y,z)\in S\}$为$R$与$S$的合成。关系的合成满足结合律与分配律。
  设$X$是集合，$R\subseteq X\times X$，定义关系的幂运算，有$R^0=I,R^1=R,R^2=R\circ R$，以此类推。

3.2 关系的闭包
  设$X$是集合，$R\subseteq X\times X$，$R$的传递闭包是包含关系$R$的最小传递关系，记作$$R^{+}=\bigcap R^{\prime }$$其中$R\subseteq R^{\prime }$且$R^{\prime }$是传递关系。$R^{+}$是一个传递关系，描述了集合内非传递性的所有关系之间的联系。
  具体的，考虑计算机网络在多地之间相连，认为两地之间直接相连为关系$R$。考虑存在两地不直接相连，由于网络相连的关系$R$不具有传递性，那么为了表达该两地虽然没有关系但仍然网络可通信的状态，就通过构造传递关系的闭包$R^{+}$来描述这种联系。
  关系$R$描述了集合种两元素之间存在关系，那么$R^n$描述了集合中通过多次关系而存在关联的元素，那么传递闭包也可以表示为$$R^{+}=\bigcup _{i=1}^{\infty }{R}^i$$  设$X$是集合，$R\subseteq X\times X$，$R$的自反传递闭包定义为传递闭包与集合的关系中自反关系的并集，记作$$R^{\ast }=R^0\cup R^{+}$$其中，$R^0$表示集合的关系中所有的自反关系。

3.3 关系矩阵
  设$X,Y$是集合，$R\subseteq X\times Y$，$|X|=m$，$|Y|=n$，取矩阵${\mathbf{B}}_{m\times n}$，对于$x\in X,y\in Y$，若有$xRy$，${\mathbf{B}}_{xy}=1$，称该矩阵为关系$R$的布尔矩阵。
  给定关系$R$与$S$，相应的布尔矩阵之间的运算如下：
  -$R\cap S$，${\mathbf{B}}_{R\cap S}={\mathbf{B}}_R\wedge {\mathbf{B}}_S$；
  -$R\cup S$，${\mathbf{B}}_{R\cup S}={\mathbf{B}}_R\vee {\mathbf{B}}_S$；
  -$R\circ S$，${\mathbf{B}}_{R\circ S}={\mathbf{B}}_R\circ {\mathbf{B}}_S$，其中定义布尔矩阵的乘法为${\mathbf{B}}_{R\circ Sij}={\bigvee }_{k=1}^p({\mathbf{B}}_{Rik}\wedge {\mathbf{B}}_{Skj})$；
  -$R^n$，${\mathbf{B}}_{R^n}={\mathbf{B}}_R^n$;
  -$R^{+}$，${\mathbf{B}}_{R^{+}}={\bigvee }_{i=0}^n{\mathbf{B}}^i$。
  当使用图表达集合$X$上的二元关系$R$时，就形成了$(X,R)$的数学模型，称为图。关系矩阵是表达图的重要方式。

3.4 等价关系
  设$X$是集合，$R\subseteq X\times X$，如果$R$是自反的、对称的、传递的，则称$R$是$X$上的等价关系。矩阵的等价、相似与合同均是一种等价关系。
  设$X$是集合，$R\subseteq X\times X$且$R$是等价关系，那么$\exists y\in X$，使得$[y]=\{x|xRy\}$，称为$y$的等价类。等价类描述了与一个元素具有等价关系的元素集合，那么对于$x,y\in X$，要么$[x]=[y]$，要么$[x]\cap [y]=\varnothing$。
  考虑自然数集合$N$，与$N$上的等价关系$mod3$，那么该等价关系的所有等价类为$[0],[1],[2]$。
  设$X$是集合，$\mathcal{X}$是$X$的所有非空子集构成的集合，那么若满足$A\cap B=\varnothing ,\forall A,B\in \mathcal{X}$且${\bigcup }_{A\in \mathcal{X}}=X$，则称$\mathcal{X}$是$X$的一个划分。给定一个集合的划分，可以唯一的确定一个等价关系。

3.5 偏序关系
  设$X$是集合，$R\subseteq X\times X$，如果$R$是自反的、反对称的、传递的，则称$R$是$X$上的偏序关系。存在偏序关系的集合称为偏序集，记作$(X,\le )$。
  设$X$是集合，$\le \subseteq X\times X$，$\forall x,y\in X$，要么$x\le y$，要么$y\le x$，则称$\le$是$X$上的全序关系。若$X$集合的$\le$是全序关系，则$(X,\le )$称为全序集，也称为链。

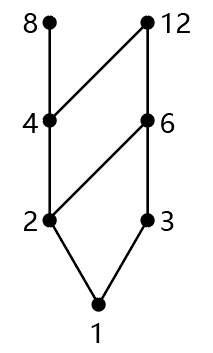
  使用图的形式表示偏序关系，使用图的上下方向表示偏序的反对称性，使用顶点表示偏序关系的自反性，使用图的边表示偏序的传递性，从而形成描述偏序关系的图，称为哈塞【Hasse】图。例如集合$A=\{1,2,3,4,6,8,12\}$上的偏序关系$(A,|)$，其哈塞图为

  假设偏序集$(X,\le )$，其中$A\subseteq X$，若$\exists a\in X$，使得$\forall x\in A$，都有$x\le a$，则称$a$是$A$的上界；反之，称为下界。
  假设偏序集$(X,\le )$，其中$A\subseteq X$，若$\exists a\in A$，使得$\forall x\in A$，都有$x\le a$，则称$a$是$A$的最大元；反之，称为最小元。
  假设偏序集$(X,\le )$，其中$A\subseteq X$，如果$A$的上界有最小元$a$，则$a$是$A$的上确界，记为$supA$；反之，称为下确界，记为$infA$。
  假设偏序集$(X,\le )$，其中$A\subseteq X$，若$\exists a\in A$，使得$\forall x\in A$，都有$a\nleqq x$，则称$a$是$A$的极大元；反之，称为极小元。

  假设偏序集$(X,\le )$，其中$A\subseteq X$，如果$(A,\le )$是全序集，则称$A$是链；若对于$\forall x,y\in A$，都有$x\nleqq y$且$y\nleqq x$，称为$A$是反链。

---

四、无穷及其基数
  关于集合的理论是19世纪末开始形成的。当时德国数学家康托尔试图回答一些涉及无穷量的数学难题，例如整数究竟有多少、一个圆周上有多少点等等。而整数、圆周上的点等都是集合，因此对这些问题的研究就产生了集合论。集合论对无穷做出了深刻的抽象。

4.1 可数集与无穷集
  设$X,Y$是集合，若存在双射映射$\varphi :X\to Y$，则称集合$X$与$Y$对等，且称与自然数集$N$对等的集合为可数集。可数集中的元素可以排列成无重复项的无穷序列。
  可数集具有如下性质：
  -对于任意无穷集，其均包含一个可数集；
  -任一可数集的无穷子集一定是可数集；
  -可数多个可数集的并集也是可数集；
  -无穷多个有穷集的并集至多是可数集；
根据以上性质，考虑全体有理数$Q=\{0\}\cup Q_{+}\cup Q_{-}$，其中$Q^{+}=p/q$，且$Q^{+}$与$Q^{-}$是对等的。对于特定的$q$，有集合$$Q_q=\{1/q,2/q,...\}$$$Q_q$是一个可数集，且$$Q^{+}=\bigcup _{q=1}^{\infty }{Q}_q$$即$Q^{+}$是可数多个可数集的并，也是可数的。那么$Q$显然也是可数的。
  集合$X=\{0,-1,1,-2,2,...\}$是一个可数集，其与$N=\{0,1,2,3,4,...\}$是双射的，但是虽然$N\subseteq X$，却又是双射的，这就形成了整体大于部分的伽利略悖论。这就形成了无穷的理念：若集合$X$能与$X$的真子集对等，那么称$X$是无穷集。

4.2 连续统集
  并非所有的无穷集都是可数集，典型的，$[0,1]$是一个不可数的无穷集。考察其可数性，假设$[0,1]$是可数的，其中$0.5$可以表示为$0.5000...$或$0.4999...$，这两者是等价的。为了保证集合元素的唯一性，假设除了$1.0=0.999...$外，其他数的某一位起之后不可以均是9，那么$[0,1]$的所有元素唯一，那么$[0,1]$的元素可列如下：$$\begin{gathered} a_1=0.a_{11}{a}_{12}{a}_{13}... \\ {a}_2=0.a_{21}{a}_{22}{a}_{23}... \\ ... \end{gathered}$$令$b=0.b_1{b}_2{b}_3...$，其有$$b_i=\{\begin{array}{rlrl}& 0,& & a_{ii}\ne 0\\ & 1,& & a_{ii}=0\end{array}$$那么$\forall k\in N$，对于上述列出的对应项$0.a_{k1}{a}_{k2}{a}_{k3}...$，都有$b_k\ne a_{kk}$，使得$b\ne a_k$，又$b\in [0,1]$，故对于列出的$[0,1]$中的元素，总能找到一个不在列中。因此$[0,1]$是不可数无穷集。
  与$[0,1]$对等的集合称为连续统集。连续统集具有如下性质：
  -可数多个连续统集的并集也是连续统；
  -多个连续统的笛卡尔积也是连续统；
  从计算机科学的角度讲，0与1的无穷序列的全体是连续统。设集合$X=\{0,1\}$，那么0与1的无穷序列为$X\times X\times ...$，考虑特征函数$f:N\to \{0,1\}$，那么0与1的无穷序列可以看作$\{f|f:N\to \{0,1\}\}$，其意义为全体自然数映射为0或1的所有特征函数，其可以看作以0为二进制整数部分，0或1的无穷序列为二进制小数部分的实数，即对等于$[0,1]$。
  根据连续统的笛卡尔积的性质，二维平面的点集与$[0,1]$对等。

4.3 基数
  设$A$为集合，那么与$A$对等的所有集合形成的集族，称为$A$的基数，记作$|A|$。
  设$A,B$为集合，若$A$与$B$的真子集对等，但$A$与$B$不对等，那么记$|A|<|B|$；若$A$与$B$对等，那么记$|A|=|B|$。

  设$A$为集合，那么$|A|<|2^A|$，称为康托【Cantor】定理。
  考察康托定理，存在$B=\{\{x\}|x\in A\}\in 2^A$，使得$|A|=|B|$，即$A$与$2^A$的真子集对等；再考察$A$与$2^A$的不对等，如若不然，则$\exists f,f:A\to 2^M$是双射的，即$$\forall x\in A,f(x)\in 2^A$$即$f(x)\subseteq A$。由于$x\in A,f(x)\subseteq A$，那么要么$x\in f(x)$，要么$x\notin f(x)$。令$$T=\{x|x\notin f(x),x\in A\}$$由于$f$是双射的，故必然存在$b,g$，使得$$f(b)=\varnothing ,f(g)=A$$那么$b\in T$，有$$T\subset A,T\in 2^A$$且$$\exists a\in A,f(a)=T$$那么对于$a$，如果$a\in f(a)$，那么$a\notin T$，但又有$a\in f(a)=T$；如果$a\notin f(a)$，那么$a\in T$，但又有$a\in T=f(a)$，结论矛盾，因此$A$与$2^A$的不对等。综上，有$|A|<|2^A|$。

  设$A,B$为集合，设映射$f:A\to B,g:B\to A$，若$f,g$都是单射，那么$A$与$B$对等，称为康托-伯恩斯坦【Cantor-Bernstein】定理。
  考察康托-伯恩斯坦定理，要使得定理成立，有$D\subseteq A$，使得$$A-D=g(B-f(D))$$即$$D=A-g(B-f(D))$$令$P=A-g(B)$，$P\subseteq D$，那么有$$P\subseteq D=A-g(B-f(D))\subseteq A-g(B-f(P))$$设映射$\varphi :x\to A-g(B-F(x))$，即$\varphi :2^A\to 2^A$，那么有$$E\subseteq \varphi (E)$$取$D_e=\{E|E\subseteq A,E\subseteq \varphi (E)\}$，那么$$D=\bigcup _{E\in D_e}E$$

  设$A,B$为集合，设映射$f:A\to B,g:B\to A$，那么$$\begin{gathered} \exists A=A_1\cup A_2,A_1\cap A_2=\varnothing \\ \exists B=B_1\cup B_2,B_1\cap B_2=\varnothing \end{gathered}$$使得$f(A_1)=B_1,g(B_2)=A_2$，称为巴拿赫【Banach】映射划分定理。

  设$(A,\le )$是一个偏序集，其每一个子集都有上确界，有映射$f:A\to A$，使得$\forall x,y\in A$，对于$x\le y$，若均有$f(x)\le f(y)$，称$f$为单调函数，且$\exists z\in A$，使得$f(z)=z$，称为塔斯基【Tarski】不动点定理。

  对于可数集$N$，定义$|N|={\mathcal{N}}_0$，连续统集$R$，定义$|R|={\mathcal{N}}_1$。
  无穷的基数运算法则如下：$$\begin{gathered} {\mathcal{N}}_0+{\mathcal{N}}_0={\mathcal{N}}_0 \\ {\mathcal{N}}_0+{\mathcal{N}}_1={\mathcal{N}}_1 \\ {\mathcal{N}}_1+{\mathcal{N}}_1={\mathcal{N}}_1 \\ {\mathcal{N}}_0{\mathcal{N}}_0={\mathcal{N}}_0 \\ {\mathcal{N}}_0{\mathcal{N}}_1={\mathcal{N}}_1 \\ {\mathcal{N}}_1{\mathcal{N}}_1={\mathcal{N}}_1 \\ {2}^{{\mathcal{N}}_0}={\mathcal{N}}_1 \\ {2}^{{\mathcal{N}}_1}={\mathcal{N}}_2 \end{gathered}$$其中，$2^{{\mathcal{N}}_0}$的意义为可数集的全体子集形成的集族，即为连续统，且根据康托定理，也可得到${\mathcal{N}}_0<2^{{\mathcal{N}}_0}={\mathcal{N}}_1$。