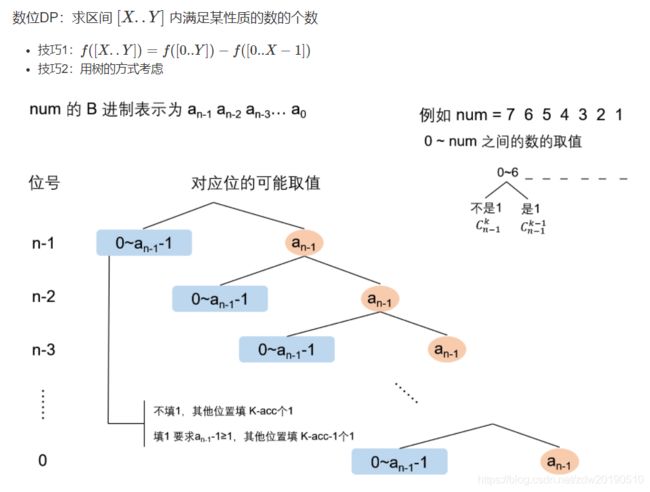
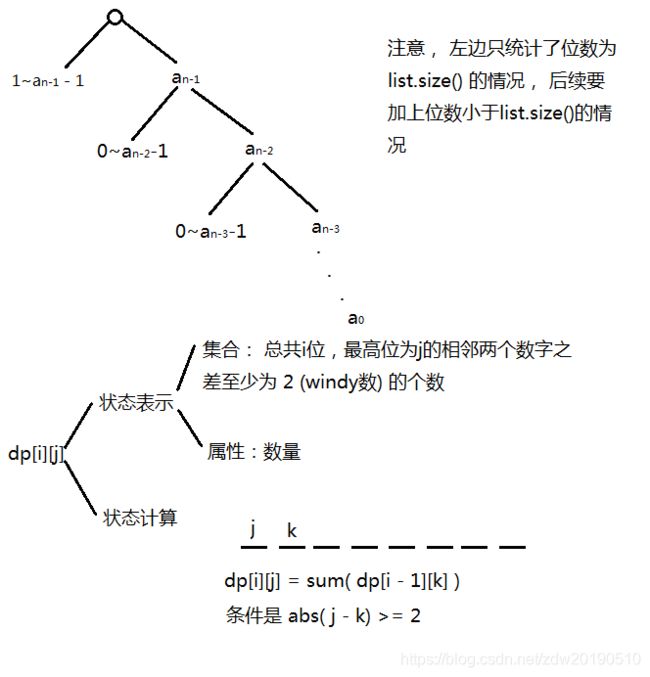
动态规划-数位DP-知识和习题

数位DP分析的大致流程

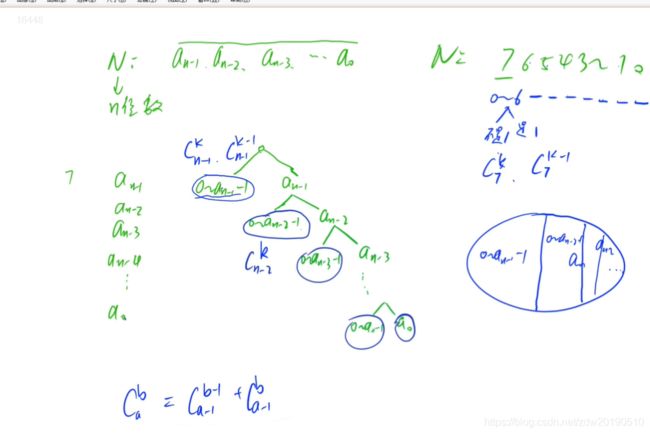
AcWing 1081. 度的数量

题目

传送门：AcWing 1081. 度的数量533人打卡

输入样例：

15 20
2
2

输出样例：

3

题解

代码

// https://www.acwing.com/activity/content/code/content/510964/
#include 
#include 
#include 
#include 

using namespace std;

const int N = 35; //位数

int f[N][N]; // f[a][b]表示从a个数中选b个数的方案数，即组合数

int K, B; //K是能用的1的个数，B是B进制

//求组合数：预处理
void init() {
     
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
            if (!j)
                f[i][j] = 1;
            else
                f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
}

//求区间[0,n]中的 “满足条件的数” 的个数
//“满足条件的数”是指：一个数的B进制表示，其中有K位是1、其他位全是0
int dp(int n) {
     

    if (n == 0)
        return 0;

    vector<int> nums;
    while (n)
        nums.push_back(n % B), n /= B;

    int res = 0; //答案：[0,n]中共有多少个合法的数

    //last在数位dp中存的是：右边分支往下走的时候保存前面的信息
    //遍历当前位的时候，记录之前那些位已经占用多少个1，那么当前还能用的1的个数就是K-last
    int last = 0;

    //从最高位开始遍历每一位
    for (int i = nums.size() - 1; i >= 0; i--) {
     

        int x = nums[i]; //取当前位上的数

        if (x > 0) {
      //只有x>0的时候才可以讨论左右分支

            //当前位填0，从剩下的所有位（共有i位）中选K-last个数。
            //对应于：左分支中0的情况，合法
            res += f[i][K - last]; //i个数中选K-last个数的组合数是多少，选出来这些位填1，其他位填0

            if (x > 1) {
     
                //当前位填1，从剩下的所有位（共有i位）中选K-last-1个数。
                //对应于：左分支中填1的情况，合法
                if (K - last - 1 >= 0)
                    res += f[i][K - last - 1]; //i个数中选K-last-1个数填1的组合数是多少

                break; //对应于：左分支中其他情况（填大于1的数）和此时右分支的情况（右侧此时也>1），不合法！！！直接break。
            } else {
     
                // 此时x是1，只能填1，更新last
                last++;
                //如果已经填的个数last > 需要填的个数K，不合法break
                if (last > K)
                    break;
            }
        }
        // 最右侧分支上的方案：进行到底了，那么也算一种方案数，算上

        if (i == 0 && last == K)
            res++;
    }

    return res;
}

int main() {
     
    init();
    int l, r;
    cin >> l >> r >> K >> B;
    cout << dp(r) - dp(l - 1) << endl;
}

AcWing 1082. 数字游戏

题目

传送门：AcWing 1082. 数字游戏

输入样例：

1 9
1 19

输出样例：

9
18

题解

代码

// https://www.acwing.com/activity/content/code/content/515735/
#include
#include
#include
#include

using namespace std;
const int maxn = 15;

int f[maxn][maxn];//f[i][j]表示最高位是j并且一共有i位的不降数的集合

void init() {
     
    for (int i = 0;i <= 9;i++) f[1][i] = 1;

    for (int i = 2;i < maxn;i++)
        for (int j = 0;j <= 9;j++)//j要从0开始
            for (int k = j;k <= 9;k++)
                f[i][j] += f[i - 1][k];
}

int dp(int n) {
     
    if (!n) return 1;

    vector<int>nums;
    while (n) nums.push_back(n % 10), n /= 10;
    int res = 0;//方案数
    int last = 0;//保留一些前缀信息，本题是上一个数是几
    ///从最大数开始枚举
    for (int i = nums.size() - 1;i >= 0;i--) {
     
        int x = nums[i];//x为当前这位数
        for (int j = last;j < x;j++)  要保障比下一位>=上一位，所以从last开始枚举,最多枚举到x,last为上一位，也即最高位，对下一位的枚举是有限制的
            res += f[i + 1][j];    ///左端的节点有i+1个位数（因为第一位的下标是0)

        if (x < last) break;//如果当前这位数比上一位小，那么后面的都不成立了，直接break退出
        last = x;

        if (!i) res++; //如果能顺利到最后一个数说明树的最右边这一段的每一个数都是小于等于前一位数的，因而++
    }

    return res;
}

int main() {
     
    init();
    int l, r;
    while (cin >> l >> r)
        cout << dp(r) - dp(l - 1) << endl;
    return 0;
}

AcWing 1083. Windy数

题目

传送门：AcWing 1083. Windy数
输入样例1：

1 10

输出样例1：

9

输入样例2：

25 50

输出样例2：

20

题解

代码

#include 
#include 
#include 
#include 

using namespace std;

const int N = 11;

int f[N][10];

void init()
{
     
    for (int i = 0; i <= 9; i ++ ) f[1][i] = 1;

    for (int i = 2; i < N; i ++ )
        for (int j = 0; j <= 9; j ++ )
            for (int k = 0; k <= 9; k ++ )
                if (abs(j - k) >= 2)
                    f[i][j] += f[i - 1][k];
}

int dp(int n)
{
     
    if (!n) return 0;

    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;

    int res = 0;
    int last = -2;
    for (int i = nums.size() - 1; i >= 0; i -- )
    {
     
        int x = nums[i];
        for (int j = i == nums.size() - 1; j < x; j ++ )
            if (abs(j - last) >= 2)
                res += f[i + 1][j];

        if (abs(x - last) >= 2) last = x;
        else break;

        if (!i) res ++ ;
    }

    // 特殊处理有前导零的数
    for (int i = 1; i < nums.size(); i ++ )
        for (int j = 1; j <= 9; j ++ )
            res += f[i][j];

    return res;
}

int main() {
     
    init();

    int l, r;
    cin >> l >> r;
    cout << dp(r) - dp(l - 1) << endl;

    return 0;
}

AcWing 1084. 数字游戏 II

题目

传送门：AcWing 1084. 数字游戏 II

题解

代码

// https://www.acwing.com/activity/content/code/content/542049/
#include 
#include 
#include 

using namespace std;

const int N = 12, M = 105;
int f[N][N][M];
int a, b, p;

int mod(int x, int y) {
     
    return (x % y + y) % y;
}

void init(){
     
    memset(f, 0, sizeof f);
    for (int i = 0; i <= 9; i ++) f[1][i][i % p] ++;

    for (int i = 2; i < N; i ++){
     
        for (int j = 0; j <= 9; j ++) {
     
            for (int k = 0; k < p; k ++){
     
                for (int x = 0; x <= 9; x ++) {
     
                    f[i][j][k] += f[i - 1][x][mod(k - j, p)];
                }
            }
        }
    }
}

int dp(int x){
     
    vector<int> nums;
    while (x) nums.push_back(x % 10), x /= 10;

    int res = 0, last = 0; // last 前面位数的和
    for (int i = nums.size() - 1; i >= 0; i --) {
     
        int x = nums[i];
        for (int j = 0; j < x; j ++) {
     
            res += f[i + 1][j][mod(-last, p)];
        } 
        last += x;
        if (!i && last % p == 0) res ++; 
    }
    return res;
}

int main(){
     
    while (cin >> a >> b >> p)init(),cout << dp(b) - dp(a) << endl;
    return 0;
}

AcWing 1085. 不要62

题目

传送门：AcWing 1085. 不要62

数据范围
1≤n≤m≤109
输入样例

1 100
0 0

输出样例：

80

题解

代码

// https://www.acwing.com/activity/content/code/content/1239002/
#include 
#include 
#include 
using namespace std;

const int N = 10;
int f[N][10];
void init(){
     
    for (int i = 0; i <= 9; i ++ ) if( i != 4) f[1][i] = 1;
    for (int i = 1; i < N; i ++ ){
     
        for (int j = 0; j < 10; j ++ ){
     
            if (j == 4 ) continue;
            for (int k = 0; k < 10; k ++ ){
     
                if (k == 4 || j == 6 && k == 2) continue;
                f[i][j] += f[i - 1][k];
            }
        }
    }
}

int dp(int x){
     
    vector<int> nums;
    if (!x) return 1;

    while(x){
     
        nums.push_back(x % 10);
        x /= 10;
    }
    int last = 1, res = 0; // last是随意，只要不是4
    for (int i = nums.size() - 1; i >= 0; i -- ){
     
        x = nums[i];

        // 左边情况
        for (int j = 0; j < x; j ++ ){
     
            if (j == 4 || last == 6 && j == 2) continue;
            res += f[i + 1][j];
        }
        if (x == 4 || last == 6 && x == 2 ) break;
        last = x;
        if (!i) res ++;
    }
    
    return res;
}

int main() {
     
    int l, r;
    init();
    // print();
    while(cin >> l >> r, l || r){
     
        cout << dp(r) - dp(l - 1) << endl;
    }
    
    return 0;
}

AcWing 1086. 恨7不成妻

题目

传送门：AcWing 1086. 恨7不成妻

输入样例：

3
1 9
10 11
17 17

输出样例：

236
221
0

题解

代码