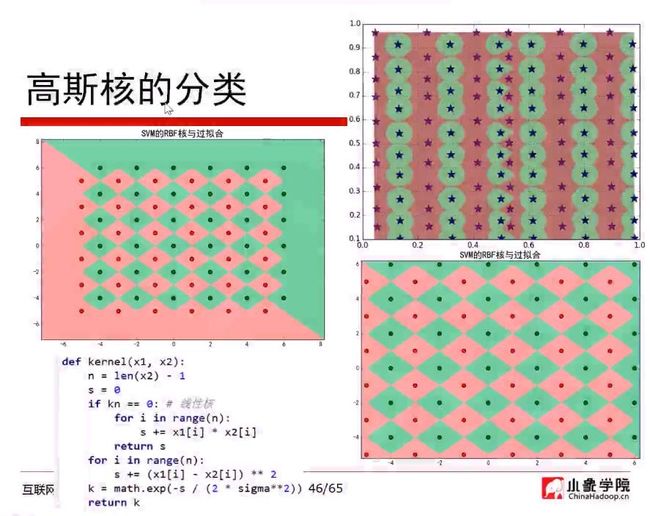
核函数
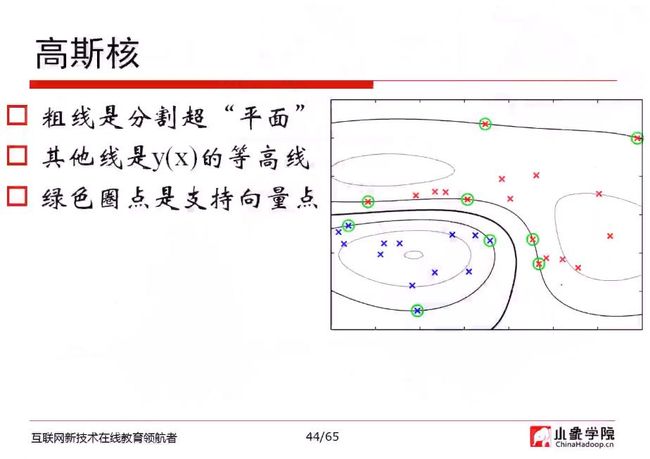
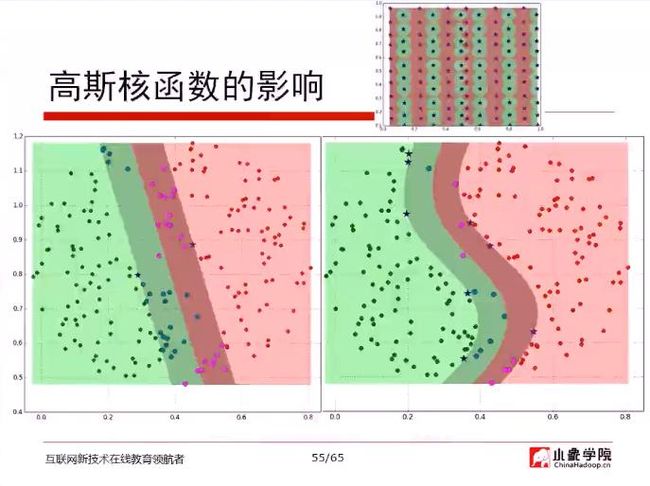
往往会选择高斯核函数
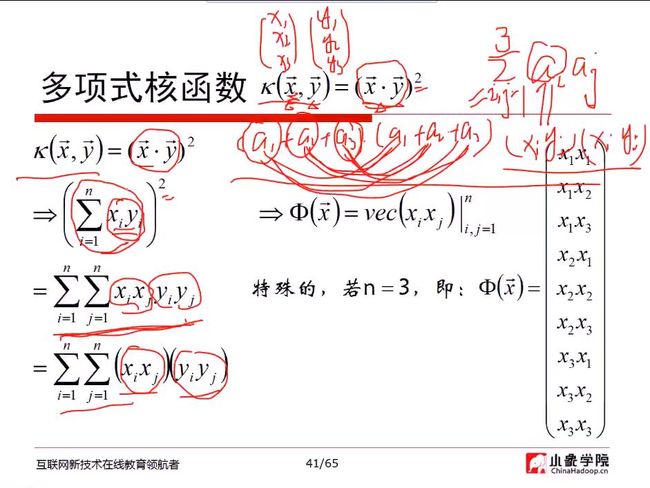
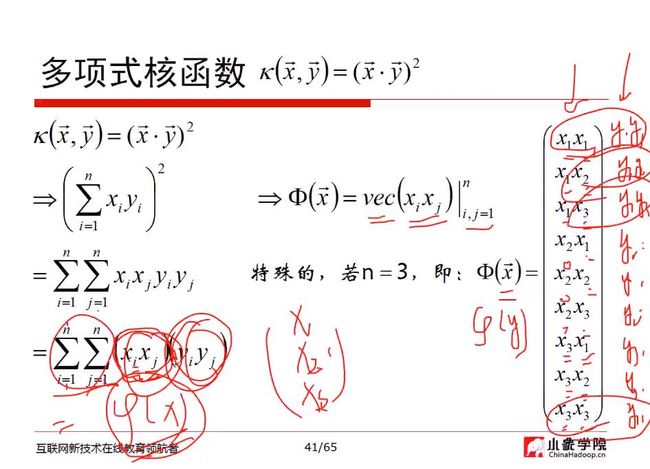
映射关系两个不同变量之间求点乘,将其定义为核函数
如果n=3,则此多项式核函数有9+3+1=13个特征
多项式核函数,把原函数映射成平方或更高次的维度
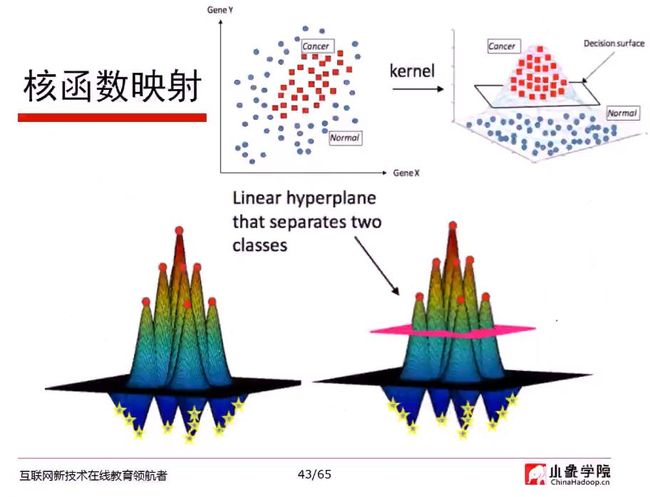
如图,根据原有SVM,无法将cancer样本区分出来,所以需要利用核函数,将cancer样本升维,其他样本降维,通过线性方式分开
利用泰勒展式展开,即形成第二行的算式
高斯核函数,把原始的函数映射成无穷维
先求φ,再去做映射是不可能的
高斯核函数->将线性的变成非线性
问:几种核函数的使用和数据集分布有关么?
答:可以无脑式的先试试高斯核函数,但是有些时候不见得一定使用高斯核函数,有些时候使用多项式核函数就够了。
实践中做一些探索性的项目,可以用SVM做图像分类,可以解决问题,也很稳定,不一定需要神经网络。但是用高斯核函数,在训练集很好,测试集却过不了。然后改成多项式核函数,就能把事情做得很好。
所以根据实践情况,来确定是否合适。
即如果没有太多的先验知识,可以先用高斯核函数,但是在训练集效果好,测试集效果不好,如过拟合,可以试着退回不太强的核函数,即多项式核函数。也许能得到更好的效果。
问:无穷维怎么算?
答:高斯核函数隐藏着φ(x),相当于帮我们做了无穷维。(保证半正定)
问:SVM做OCR合适么?
答:在现在的情况不一定合适。假定做中文的OCR,字符集成千上万,假定有一万个常用字,则需要做一万个分类。分类数量增多,SVM效果会降下去。只能说有一定的可能性,但不一定非常合适。
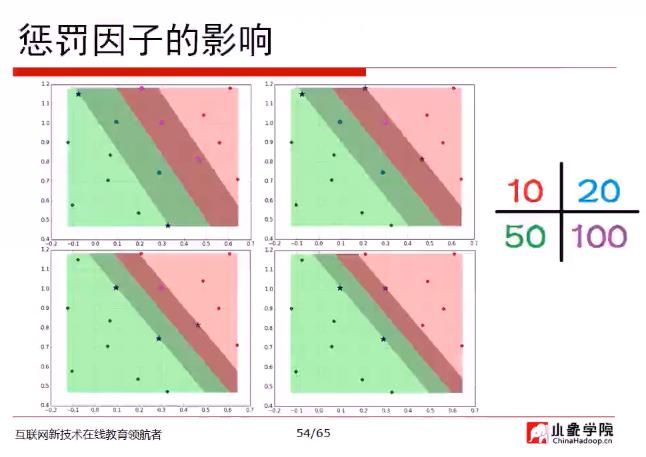
惩罚因子越小,抗过拟合能力越强,宽度越大
问:(xgboost的问题)用6分类的数据,训练集与测试集分开。为何出现过拟合?训练集准确率非常高,可是测试集非常差,请问如何改进?
答:可以尝试减少树的深度,增大λ的阻尼值
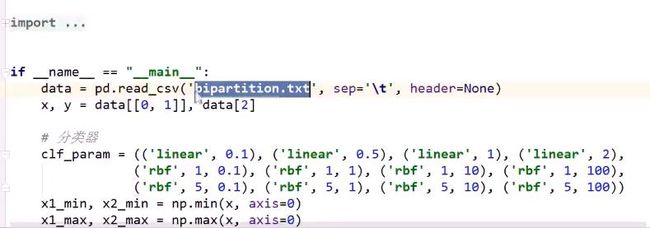
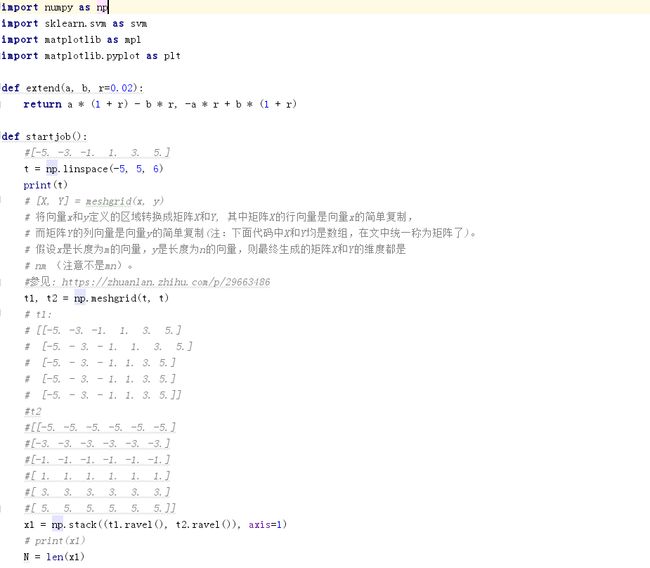
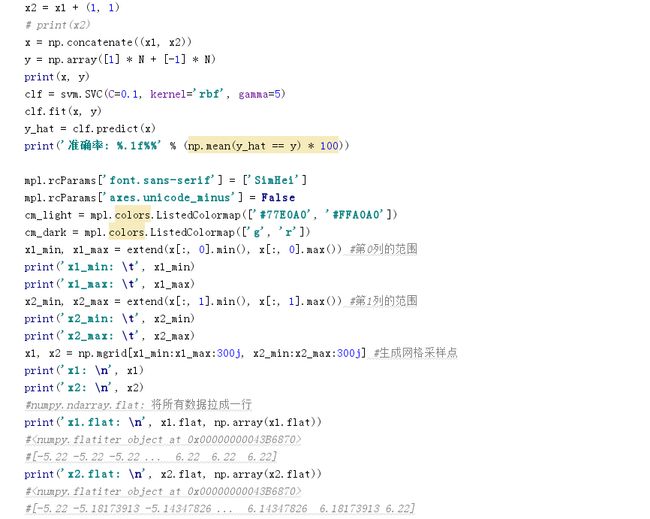
Python代码实践
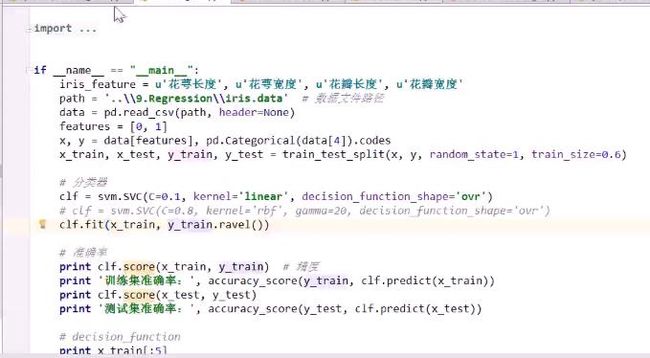
1. 鸢尾花代码
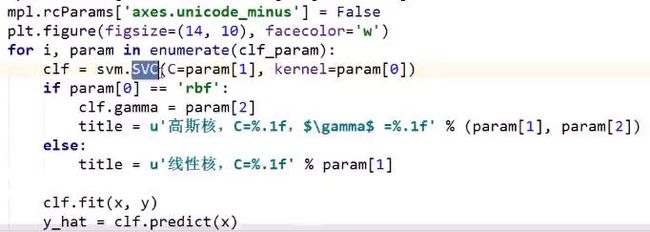
SVC指:支撑向量分类器(Support Vector Classifier)
C取0.1,意味着α是从0~0.1
kernel: linear, 意味着使用线性核函数
decision function: 以鸢尾花三分类为例,给出某一个样本属于哪个类别的可能是比较大的
decision_function_shape: ovr,one_vs_rest。
得到三个SVM,根据得分大小,进行分类
2. decision_function
SVM多分类器实现,用若干个二分类器,合成一个多分类器
可以加入np.set_printoptions(suppress=True),控制numpy的输出
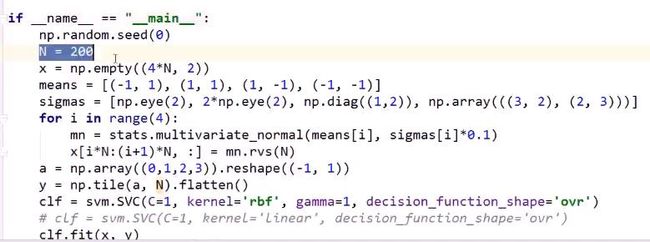
scipy的:stats.multivariate_normal: 多元正态分布,将均值与方差喂给此函数,即可得到模型
用此模型调用rvs,即动态随机采样(Random Variable Sample)
sigmas * 0.1的目的:方差不要太大,有利于各个点分散一些,不要太聚在一起
a = np.array((0, 1, 2, 3)).reshape((-1, 1))的目的,是将a转换为:
arrary([[0],
[1],
[2],
[3]])
的形式。
np.tile方法:如np.tile(a, N),即将arrary:a,复制N次,得到新的array。
如y = np.tile(a. 2),则得到:
array([[0, 0],
[1,1],
[2,2],
[3,3]])
然后,我们对y做flatten,即做拉伸,得到新的array:
array([0,0,1,1,2,2,3,3])
等同于y.reshape(-1,)
这个目的就是得到分类向量y
svm的核函数使用的是高斯RBF, decistion function shape使用的是ovr: one-vs-rest,如果是4分类,则会输出多行4列的矩阵。
还有一个类别是ovo: one-vs-one,从四个类别之间两两之间做分类器,其实需要6个值(12,13,14,23,24,34)。即decision_function输出会是多行6列的矩阵。
取得分最大的列索引为分配的类别
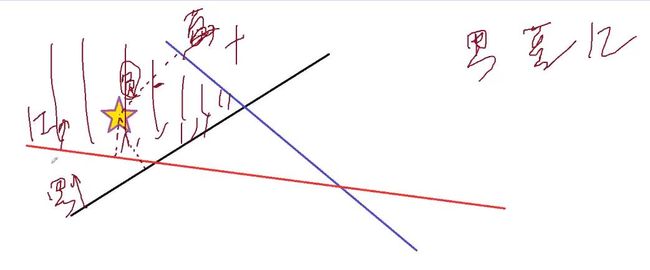
穿插讲解如何分类
五角星相比蓝线距离是负数,相比红线与黑线距离是正数。
而五角星到黑线距离更远,则分类会将五角星分类到黑线类别
PS: 负数代表不可能属于这个类别
decision_function,会输出各个类别的得分,取得分最大的索引为分配的类别。
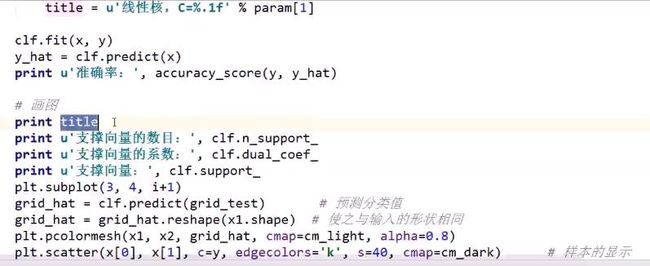
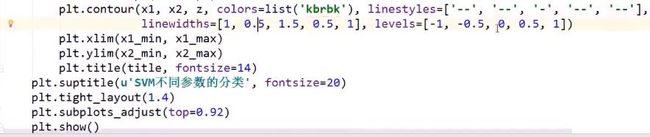
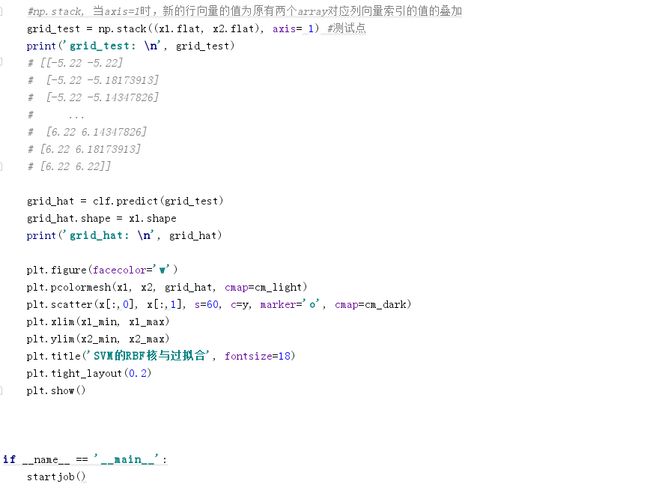
3. SVM_draw
此截图,方便看全plt.scatter的所有参数
另一种简洁绘制方式:
4. ClassifierIndex
以预测疾病为例进行解释:
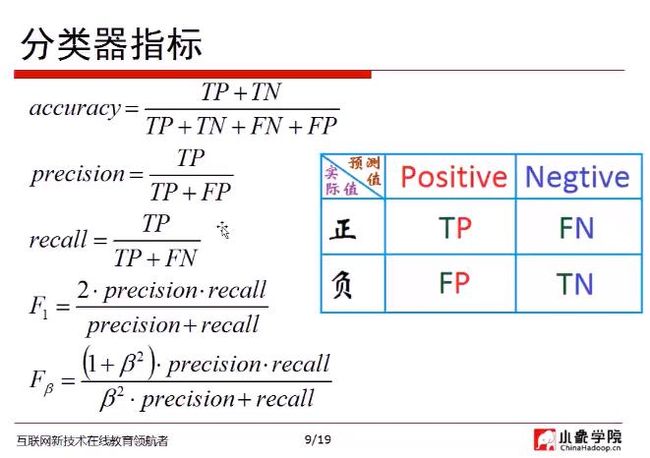
精度(accuracy):将得病与未得病做对的预测/总样本个数
准确率(precision): 被诊断得病的样本个数/被诊断得病的样本个数+错误诊断得病的样本个数
召回率(recall): 被诊断得病的样本个数/被诊断得病的样本个数+得病但是没有被诊断得病的样本个数
Precision与Recall不可能同时增大,因此需要做加强,F1与Fβ就是做这个事情
如果β^2是∞,则Fβ就是Recall,如果β趋近于0,则Fβ趋近于Precision
F1是什么呢?当然就是β为1时的公式啊
实际数据:
4正 2负
预测
正 负
TP:3 FN:1
FP:2 TN:0
所以,
accuracy = (3 + 0) / (3 + 1 + 2 + 0) = 0.5
precision = 3 / 3 + 2 = 0.6
recall = 3 / 3 + 1 = 0.75
代码示例
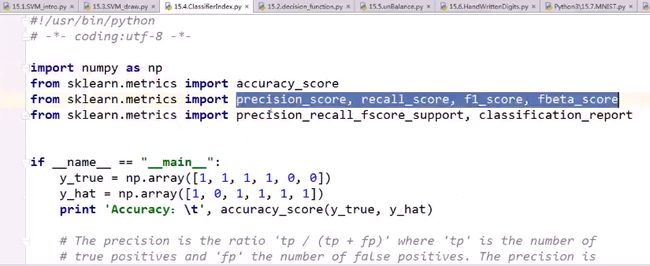
sklearn的metrics中,已经内置了precision, recall, f1, fbeta的计算类,可以直接使用
classification_report,可以将precision, recall, f1-score, support的值,根据各个分类,整体输出为一张表。非常方便。
5. unBalance
class_weight的参数:因为1的样本数据只有10个,所以权重设置很大,如class_weight={-1:1, 1:99}。但是设置为99未必一定好,设置为10其实效果也不错,或者说堪用了,不会完全过拟合。
问:如果样本不均衡比例达到1000:1,是不是只能通过增加样本来建模?
答:1000:1的情况是普遍存在的,比如金融欺诈数据。是的,实在搞不定,只能这样了
6. HandWrittenDigits
数据下载地址:http://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/
一行数据表示一副图片:每行65个数字,前64个数字代表8x8的小图片,其数值代表黑色的强度:0~16,第65个数字代表对应的数字。
使用SVM,即是十分类问题
此处取高斯核,为了稳妥一些,gamma值足够小,相当于近似线性核
7. MNIST
28x28的图像,数据下载地址为:https://pjreddie.com/projects/mnist-in-csv/
数据集第一列是代表的数字,之后28x28列的数字,代表数字各个点的黑度
所以特征集通过: data.iloc[:,1:].values获取
真实值y,通过data.iloc[:,0].values获取
因为已经有mnist_test.csv作为测试集,所以无需train_test_split这个方法将训练集进行拆分
这些代码已经经过实际调试,确保运行正常
训练集的初始图片以及代表的数字:
SVM的核函数为高斯核函数
随机森林训练的速度在一分钟以内
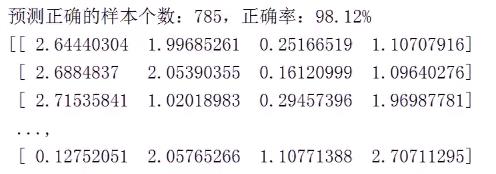
训练集的准确率在100%,随机森林确实挺强的
但是SVM训练的速度就慢得多~~~
如果说此例SVM算法的训练时间以及predict的时间,就令你怀疑人生,那是因为还没有见过训练几天几夜也结束不了的数据集与相关算法。。。
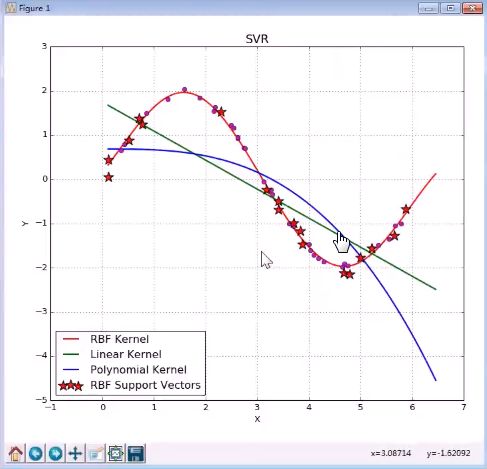
8. SVR
绘制支撑向量回归的曲线
y: 正弦的曲线,加上一点噪声,噪声给的大一些,样本会随着曲线抖动的厉害一些
如果不要噪声,则构建完全在线的数据
很显然,在这个例子,多项式核的能力是让我们吃惊的。完全没有按照正弦趋势走。
而SVR,高斯核,则体现出正弦曲线的趋势
问:SVR的损失函数?
答:SVR的损失函数与SVC的损失函数一致的。仍然是我们计算预测值和实际值误差的平方,作为它的损失值。但是这个值离的近的话,依然给它更大的损失;如果这个值足够远,就不要给它损失了。
9. Grid
问:随机森林在实际应用中,要把所有输入特征离散化么?
答:这个根据具体情况。比如用随机森林做了鸢尾花数据的分类,而鸢尾花数据,事实上是连续的。所以不见得所有特征都要做离散化