1 最小生成树
1.1 Kruskal算法
选n-1条边
- 初始化:建立一个边的数组,并根据权值排序。
- 选边:选择权值最小的,且两端点不在同一集合(回路)的边。
- 重复2,直到所有边遍历完。
核心代码
int kruskal(vector e) {
makeSet();
int sum = 0;
for (int i = 0; i 主函数调用:定义edge类,生成edge的数组,并排序
#include
#include
#include
#define INF 10000
using namespace std;
//定义一个edge类
class edge {
public:
int val;
int start;
int end;
edge(int v, int x, int y) {
val = v;
start = x;
end = y;
}
};
bool cmp(edge a, edge b) {
return a.val < b.val;
}
//图
const int N = 6;
int graph[N][N] = { { INF,7,4,INF,INF,INF },
{ 7,INF,6,2,INF,4 },
{ 4,6,INF,INF,9,8 },
{ INF,2,INF,INF,INF,7 },
{ INF,INF,9,INF,INF,1 },
{ INF,4,8,7,1,INF }
};
int main() {
//遍历图,生成边的集合
vector e;
for (int i = 0; i 并查集的实现
//并查集
int father[N];
void makeSet() {
for (int i = 0; i1.2 Prim算法
选n个点
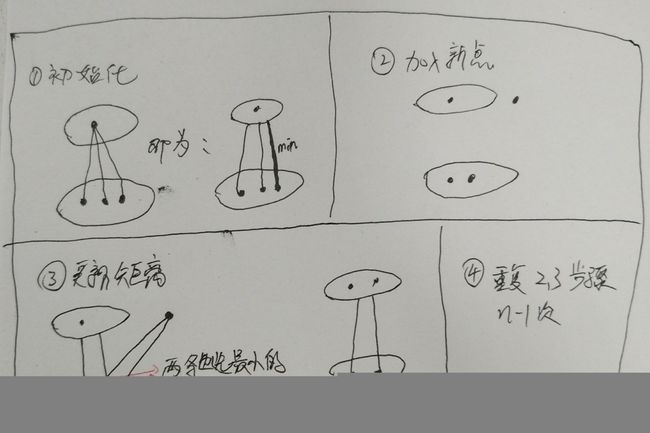
- 初始化:任意选一点作为初始顶点,标记为visit(加入集合),剩下的点与该点的距离作为到该集合的初始化距离。
- 加入新点:剩下点中,到该集合最近的点index加入到集合中。
- 更新距离:剩下点到该集合的距离d[j]=min(d[ij],graph[j][index])。
-
重复2,3步骤n-1次,即所有节点都加入到集合中。
核心代码
int prim(int cur)
{
//1.初始化
int sum = 0; //路径和
cout << cur << " ";
visit[cur] = true;
for (int i = 0; i < N; i++)
dist[i] = graph[cur][i];
for (int i = 1; i < N; i++) //4.重复取点n-1次
{
//2.选点
int minTemp = INF, index = -1;
for (int j = 0; j < N; j++)
{
if (!visit[j] && dist[j] < minTemp)
{
minTemp = dist[j];
index = j;
}
}
visit[index] = true;
cout << index << " ";
sum += minTemp;
//3.更新距离
for (int j = 0; j < N; j++)
{
if (!visit[j])
{
dist[j] = min(dist[j], graph[index][j]);
}
}
}
cout << endl;
return sum;
}
主函数调用
#include
#include
#include
#define INF 10000
using namespace std;
const int N = 6; //顶点数
vector visit(N,false); //每个顶点加入集合的标记
vector dist(N,0); //剩下顶点到集合的距离
int graph[N][N] = { { INF,7,4,INF,INF,INF }, //INF代表两点之间不可达
{ 7,INF,6,2,INF,4 },
{ 4,6,INF,INF,9,8 },
{ INF,2,INF,INF,INF,7 },
{ INF,INF,9,INF,INF,1 },
{ INF,4,8,7,1,INF }
};
int main()
{
int sum = prim(0);//从0号顶点出发
cout << sum;
system("pause");
return 0;
}
2 最短路径
2.1 Floyd算法
求任意两点之间的最短路径
void floyd()
{
for(int k=0;ke[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j];
}
}
}
2.2 Dijkstra算法
和Prim算法类似
- 初始化:以给定的s作为源点,标记为visit(加入集合),剩下的点与该点的距离作为到该该点的初始化距离。
- 加入新点:剩下点中,到s最近的点index加入到集合中。
- 更新距离:剩下点到s的距离d[j]=min(d[j],graph[j][index]+d[index])。
- 重复2,3步骤n-1次,即所有节点都加入到集合中。
void dijkstra(int cur)
{
//1.初始化剩余点到s的距离
visit[cur] = true;
for (int i = 0; i < N; i++)
dist[i] = graph[cur][i];
dist[cur] = 0;
//4.重复n-1次
for (int i = 1; i < N; i++)
{
//2.选点
int minTemp = INF, index = -1;
for (int j = 0; j < N; j++)
{
if (!visit[j] && dist[j] <= minTemp)
{
minTemp = dist[j];
index = j;
}
}
visit[index] = true;
//3.更新距离
for (int j = 0; j < N; j++)
if (!visit[j] && graph[j][index] != INF)
dist[j] = min(dist[j], graph[j][index] + dist[index]);
}
}
#include
#include
#include
#define INF 10000
using namespace std;
const int N = 6;
vector visit(N, false); //每个顶点得到最短路径的标记
vector dist(N, 0); //剩下顶点到s的距离
int graph[N][N] = {
{ INF,7,4,INF,INF,INF },
{ 7,INF,6,2,INF,4 },
{ 4,6,INF,INF,9,8 },
{ INF,2,INF,INF,INF,7 },
{ INF,INF,9,INF,INF,1 },
{ INF,4,8,7,1,INF }
};
int main()
{
dijkstra(0); //以顶点0作为源点s,更新dist数组
for (int i = 0; i