静态博弈:所有参与人同时行动
动态博弈:参与人行动有先后顺序,后行动者在先行动者做出决策之后在做出决定(eg,下棋
常用博弈树表示动态博弈
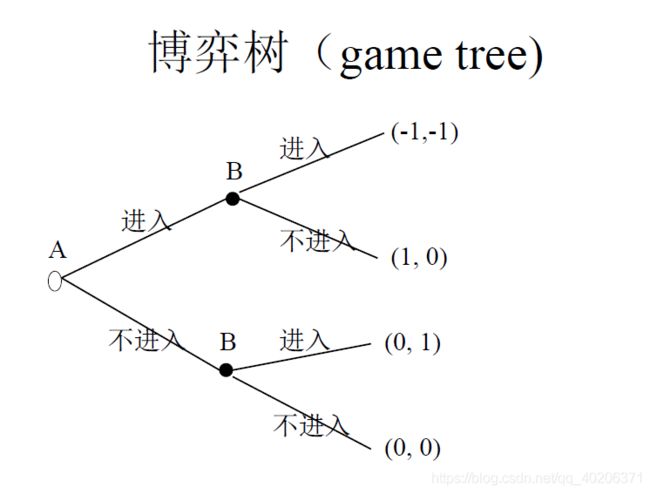
2 动态博弈
动态博弈中,事前最优的战略可能不是事后最优。(A可以按照B声明的来判断选择,也可以不按照;那么B就可以因地制宜地改变。——相机行动方案,contingent action plan)
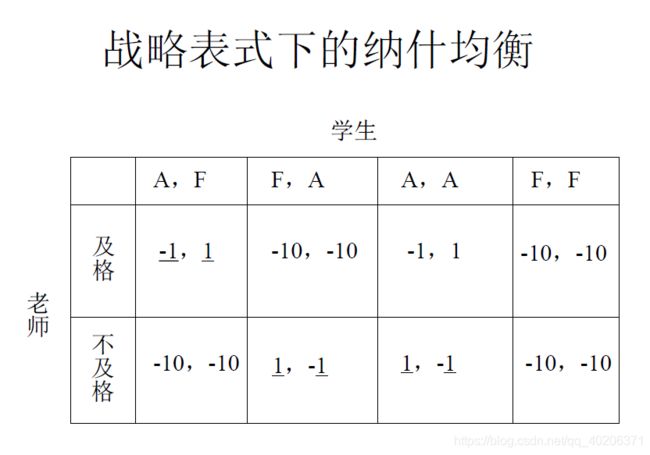
以上图为例,老师的决策是给学生打分打及格or不及格;学生事先声明,如果我及格了,我是选择A(accept)战略还是F(fighting)战略。(这个声明老师也是能看得到的)
对于上面这个表达式,我们有三个纳什均衡一个是【及格,(A,F)】,一个是【不及格,(F,A)】,另一个是【不及格,(A,A)】。
我们先看第一个纳什均衡。学生申明我采取的是(A,F)战略,老师为了不得到-10的代价,会选择给学生及格。但是退一步讲,即便老师给了不及格,学生也不会选择F战略,因为此时学生选了F战略的话,虽然老师是-10的代价了,可自己也是-10的代价,损失太大。因此,如果学生是理性的,那么即使老师给了不及格,学生也不会选择F战略。那么老师就不会受其威胁。因此,(A,F)是一个不可置信威胁。
我们再看第二个纳什均衡。学生申明我采取的是(F,A)战略,老师为了不得到-10的代价,选择了给学生不及格。但退一步讲,即使老师给了及格,学生也不会选择F战略(和(A,F)战略不可置信是一样的推导方式),因此(F,A)也不是一个可置信威胁。
最后一个纳什均衡,分析下来是可以达到的,(A,A)是一个可置信威胁。
——》动态均衡就是要排除一些不可置信的威胁。
2.1 精炼纳什均衡 perfect NE
不包含不可置信的行动的战略所组成的纳什均 衡被称为“精炼纳什均衡”。
也就是说,不论 过去发生了什么,构成精炼纳什均衡的战略, 其所规定的行动在每一个决策点上都是最优的。 所以,又称为“序惯均衡”(sequential equilibrium);
精炼纳什均衡首先必须是“纳什均衡”,但并非所有纳什均 衡都是合理的;只有其战略不包含不可置信行动的纳什均衡才是合理的。
不可置信威胁的根源是事前最优与事后最优不同,导致许多帕累托效率无法实现
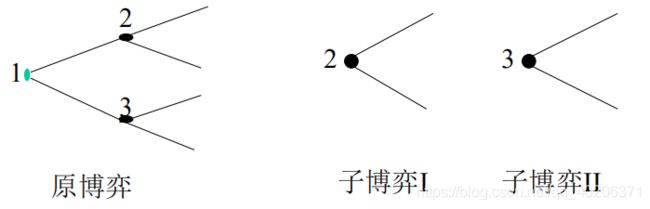
2.2 子博弈
由原博弈中某个决策点(信息集)开始的部分构成一个子博弈。
精炼纳什均衡:
( 1 )在原博弈是一个纳什均衡;
(2 )在每一个子博弈上都是纳什均衡。
2.3 逆向归纳法 backward induction
在有限博弈中,我们可以用逆向归纳法求解精炼纳什均衡:从最后一个决策点开始,找出该子博弈的纳什均衡;然后再倒回到倒数第二个决策点,找出决策者的最优决策(假定最后一个决策者的决策是最有的;如此一直到初始决策点, 所有子博弈上的最优选择就是精炼纳什 均衡。又称“rollback”。
精炼纳什均衡下所经过的决策点和最优选择构成的路径,称为均衡路径(equilibrium path);
其他的路径是非均衡路径( off-equilibrium path);
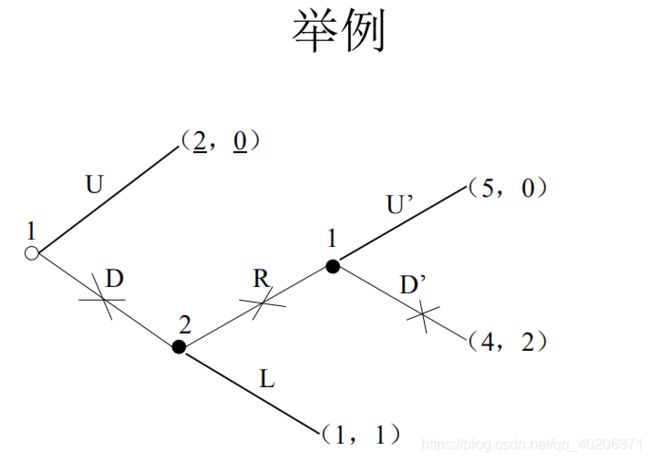
以上图为例,我们逆向归纳。先看最后一个需要博弈的对象1,他此时有两个选择,U'和D'。如果选U'的话,可以得到5;选择D'的话,可以得到4。5>4,那么(4,2)这一选择就被淘汰了。然后看2,同理可以把(5,0)淘汰(因为1>0);最后又回到1,他会选择U(因为2>0)。
所以逆向归纳法的结果为(2,0)。
2.4 理性共识
逆向归纳的过程实际上就是重复剔除劣战略的过程,其前提是博弈规则和理性
共识:每个人是理性的,每个人知道每 个人是理性的,如此等等。
因此,精炼纳什均衡的合理性取决于理性共识的合理性。
3 承诺
承诺是将不可置信的威胁变成可置信的威胁的行动:威胁不仅是事前最优的,也是事后最优
的。
承诺意味着限制自己的自由:选择少反而对自己好。但承诺也是有成本的。(eg,项羽破釜沉舟)
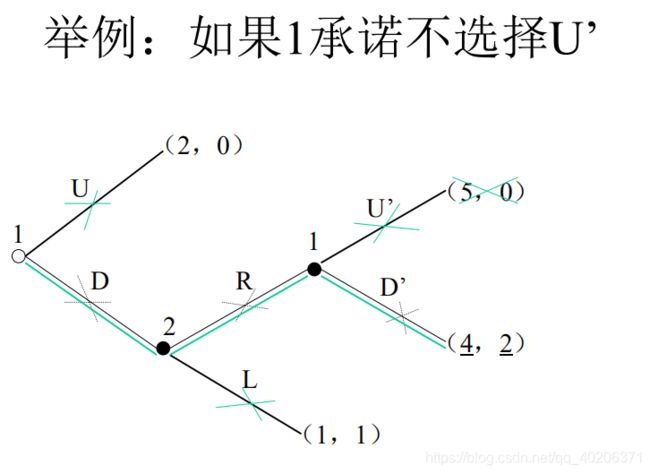
我们重新审视2.3的例子。如果1承诺不选择U'的话:此时需要被剔除的战略我们用绿色的×来表示,黑色的×表示原来被剔除的战略。此时,最后逆向归纳法的结论为(4,2)。
3.1 承诺举例
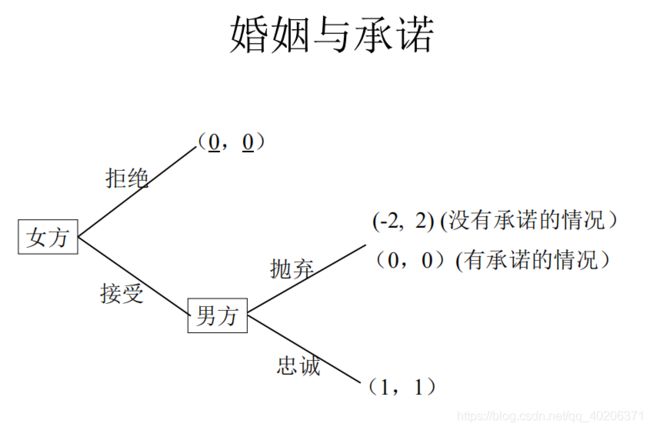
3.1.1 婚姻
->婚姻中的承诺:彩礼、昂贵的婚礼可以理解为一种对婚姻的承诺。
在这个模型下,如果没有承诺的话,男方可能就会选择“抛弃”,女方拒绝;有了承诺之后,女方接受,男方忠诚。
3.1.2 公债
D表示最大公债,r表示公债的利率,P表示政府违约的时候受到的惩罚
——>政府履约的条件:D(1+r)<=P(即违约收到的惩罚大于我吞掉公债的获得)
也就是说,政府可发行的最大公债为P/(1+r)
老百姓对政府的约束能力决定了P
——>有限(民主)政府比专制政府可以发行的公债更多
3.1.3 非升即走的大学制度
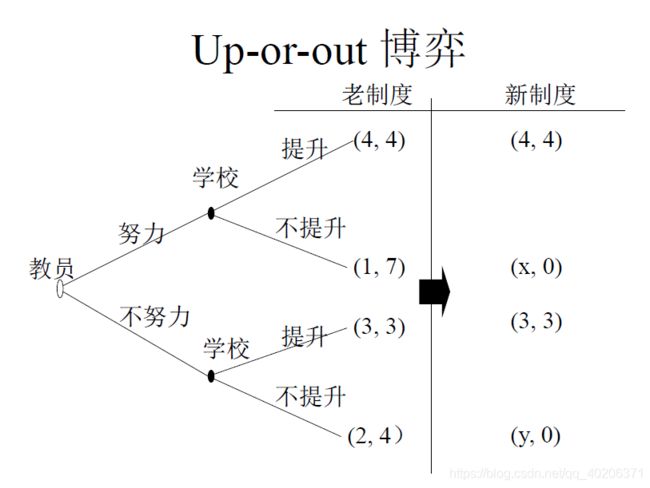
老制度下,精炼纳什均衡是不努力,不提升。
新制度下,精炼纳什均衡是努力,提升。