线性代数的本质(个人笔记)
线性代数的本质
-
- 1.什么是向量
- 2. 线性组合:张开的空间与基
- 3. 矩阵与线性变换
- 4. 矩阵乘法与线性变换复合的关系
-
- 4.1 三维空间的线性变换
- 5. 行列式
- 6.逆矩阵、列空间、秩与零空间
-
- 6.1 非方阵 不同维度空间之间的线性变换
- 7. 点积与对偶性
- 8. 叉积的标准介绍
-
- 8.1 以线性变换的角度看待叉积
- 9. 基变换
- 10. 特征值与特征向量
1.什么是向量
从物理专业学生角度看,向量是箭头
从计算机专业角度看,向量是数字列表

从数学专业来看,他们试图概括两种观点,向量可以是任何东西,只需要保证向量相加和向量数乘是有意义的即可
由此看出向量相加和向量数乘贯彻线性代数始终
c ⃗ = a ⃗ + b ⃗ \vec c = \vec a + \vec b c=a+b
c ⃗ = 2 b ⃗ \vec c = 2 \vec b c=2b
在物理专业来看,向量的起点是不固定的,我们只能通过向量的大小和方向确定向量,但是它可以在空间的任何位置存在
在线性代数中,向量的起点都是原点(坐标轴),每一个向量对应一个多元数组.在这个角度的定义下,向量加法遵循平行四边形定则(相加中的平移是线代中唯一允许移动起点的情形)。数乘会造成向量的拉伸、压缩甚至反向。我们称以上三种现象为缩放(几何角度)
2. 线性组合:张开的空间与基
在线代中,如果把向量的坐标看成标量,那么该向量是靠基向量的相加与缩放构成的。一般X、Y轴对应的基向量就是(1,0)、(0,1)。当我们选择不同的基向量就可以构成不同的坐标系
两个向量的和被称为两个向量的线性组合
由给定基向量线性组合得到所有向量的集合称为给定向量张开的集合
考虑单个向量,一般看作箭头
考虑多个向量,一般看作点(终点)
当在三维空间时,两个向量张开的空间在一个平面上

当三维空间三个向量线性组合时,会有两种情况:一种是第三个向量刚好落在两个向量组成的平面上,此时张开的空间仍然在组成的平面。另一个情况是不在平面上,第三个向量使得前两个向量张开的平面在它的方向来回移动,从而扫过整个空间
在多个向量张开的向量空间里,如果移除某个向量,张开的空间不受影响,则称为该向量是线性相关的。但如果每个向量都使空间增加一个维度,则称他们线性无关
3. 矩阵与线性变换
变换本质是函数的一种花哨说法,它接收内容并输出结果。在线性代数的情况下,我们考虑的是接收一个向量并输出一个向量的变换
线性变换必须满足两个要求:
1.直线在变换后必须仍保持直线
2.原点必须还在原位
总得来说,线性变换是保持网格线平行并等距分布的变换。比如原点的旋转(X、Y轴顺时针或逆时针旋转)
同时,只要记住了变换后的基向量位置,就可以推出任意在原坐标下的向量的新坐标位置。所以我们会将新基向量坐标组合成一个矩阵。变换后的新向量坐标就是原坐标与该矩阵的积
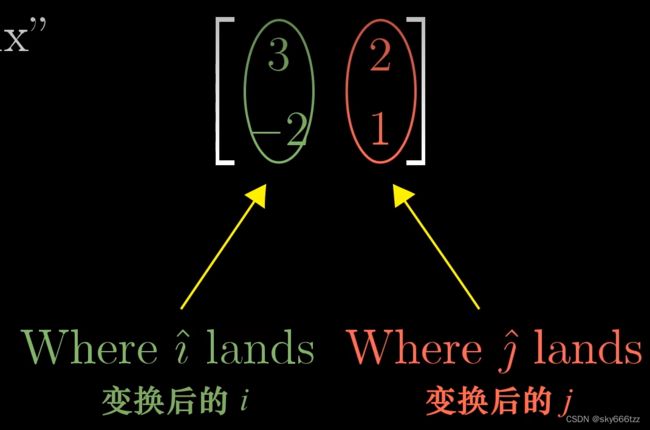
有一个术语“剪切”,代表一个基向量(1,0),另一个基向量(1,1)
由上,每次看到矩阵,都可以理解为一种空间变换
4. 矩阵乘法与线性变换复合的关系
在线性代数中,进行多次线性变换,将它们视为一次变换。这个变换就是复合变换。单个线性变换矩阵的积就是复合变换矩阵。
因此多个矩阵相乘的几何意义就是多个线性变换相互作用。但是注意变换顺序是从右到左读,类似 f ( g ( x ) ) f(g(x)) f(g(x))

[ e , g ] [e,g] [e,g]是 i ⃗ \vec i i首先到达的位置,与 M 2 M_2 M2相乘形成线性变换。同理 [ f , g ] [f,g] [f,g]是 j ⃗ \vec j j先到达的位置
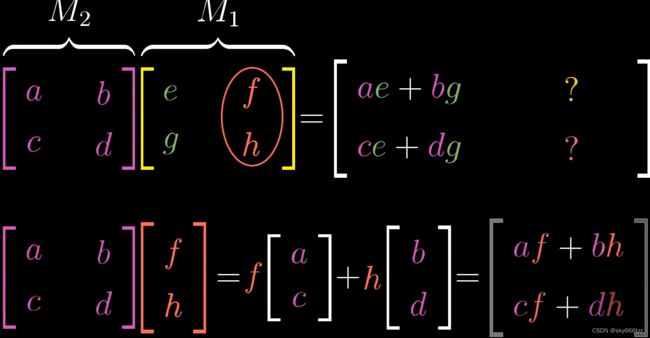
4.1 三维空间的线性变换
三维空间的线性变换也是先缩放再相加, x x x相当于基向量 [ 0 , 3 , 6 ] [0,3,6] [0,3,6]缩放 x x x倍,y、z同理

类似于之前的两个矩阵相乘,这里三维矩阵相乘也与上面的解读类似。
5. 行列式
将 [ 1 , 0 ] [ 0 , 1 ] [1,0][0,1] [1,0][0,1]组成的 1 × 1 1\times1 1×1图形看作基本的 1 × 1 1\times1 1×1正方形,那么其他向量比如 [ 3 , 0 ] [ 2 , 2 ] [3,0][2,2] [3,0][2,2]组成的图形,向量线性变换得到的新图形面积就是矩阵的行列式。
行列式也是指新图形面积的增加为原来的 X X X倍
当行列式为 0 0 0代表矩阵所用的变换将空间压缩到更小的维度上。

但是这样无法理解行列式为负的情况,将整个二维空间想象为一张纸,行列式为负数相当于将二维空间翻转一面

矩阵四个元素都不为 0 0 0就需要配合下面那张图理解

行列式在三维依然是用来描述缩放比例,但这个比例是体积的比例,聚焦 1 × 1 × 1 1\times1\times1 1×1×1的立方体的缩放。这里也可以看作体积。行列式为0意味着空间被压缩成直线、平面或者点(矩阵的列线性相关)。

我们用右手定则判断行列式正负,当空间的几何体不能用右手定则表示,那么行列式为负

通过行列式的意义可以理解矩阵( A × B A\times B A×B)的行列式 = A A A的行列式 × \times ×B的行列式
因为行列式代表面积或体积缩放的比例,最终面积改变比例 = A改变的比例 × \times × B改变的比例
6.逆矩阵、列空间、秩与零空间
线性代数可以用来解决特定的线性方程组问题

A x ⃗ = a ⃗ A\vec x = \vec a Ax=a
从几何的角度来看,我们需要找一个向量 x ⃗ \vec x x,使得通过线性变换之后可以与 a ⃗ \vec a a重合
矩阵的逆是与该矩阵对应的线性变换相反的变换。比如 A A A是顺时针旋转90°。那么 A − 1 A^{-1} A−1就是逆时针旋转90°。 A × A − 1 A \times A^{-1} A×A−1是恒等变换(什么都不做)。它对应矩阵如下,也代表基向量 ( 1 , 0 ) 和 ( 0 , 1 ) (1,0)和(0,1) (1,0)和(0,1)
1 0 0 1 \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} 1001
可以通过左乘矩阵的逆来求解方程 A x ⃗ = v ⃗ A\vec x = \vec v Ax=v,在几何上相当于 v ⃗ \vec v v在空间进行逆变换
当 A A A的行列式为 0 0 0,空间会被压缩到点或线,此时是没有逆矩阵的,因为点和线不能变成面或体。此时 x ⃗ \vec x x无论是什么方向都会转为点或线,因为 x ⃗ \vec x x只是改变向量的大小
当变换的结果是一条直线时,我们称它的秩为 1 1 1,如果变换的向量落在二维平面上,我们称这个秩为 2 2 2.由此发现秩代表变换后空间的维数(准确来说是列空间的维数)。当秩达最大值时,称为满秩(与列数相等)
矩阵的列空间:矩阵 A A A所有可能变换结果的集合(矩阵的列代表基向量变换后的位置),列空间就是这些基向量所张成的空间

零空间或核:经过矩阵变换后落在原点的集合。对线性方程组来说,当 A x ⃗ = v ⃗ A\vec x = \vec v Ax=v的 v ⃗ \vec v v为 0 0 0向量时,解就是零空间
6.1 非方阵 不同维度空间之间的线性变换
将二维转换为三维,两个基向量(2x2矩阵)转换成的三维空间是过原点的二维平面。因此 3 × 2 3 \times 2 3×2矩阵的几何意义是将二维空间映射到三维空间上

类似看到 2 × 3 2 \times 3 2×3列矩阵时,三列代表原始空间三个基向量,两行代表三个基向量在变换后用两个坐标描述,所以一定落在二维空间中,是一个三维到二维的转换
1 × 2 1 \times 2 1×2的矩阵代表两个基向量转换后到一个数轴上,转换后只有一个数,所以这个矩阵只有一行。

7. 点积与对偶性
点积的计算如下:
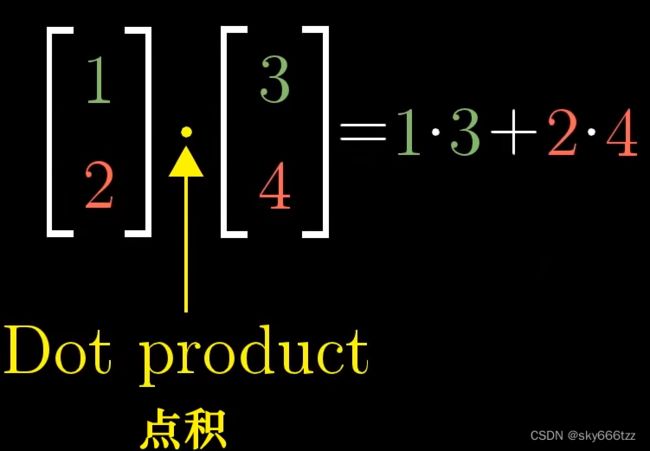
点积 w ⃗ ⋅ v ⃗ \vec w \cdot \vec v w⋅v的几何意义是 v ⃗ \vec v v(或 w ⃗ \vec w w)在 w ⃗ \vec w w(或 v ⃗ \vec v v)上的投影的长度再乘上 w ⃗ \vec w w自己的长度。当两个向量垂直,意味着投影长度是 0 0 0,那么乘积也是 0 0 0,两向量相反时,点积为负
视频中讲解了点积为什么那么计算(我个人也是看得懵).写一点自己的理解
点积的计算过程与 1 × n 1 \times n 1×n矩阵与 n n n维向量矩阵乘法的过程一样
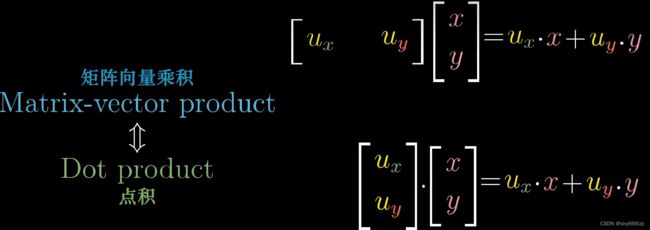
对于某个向量 u ⃗ \vec u u,把它视作基向量,它的投影矩阵是 [ u x u y ] [u_x \quad u_y] [uxuy],其他向量想要线性转换到与它为基向量的空间必须与该矩阵相乘,计算的表达式是 u x × x + u y × y u_x\times x + u_y \times y ux×x+uy×y与点积 u ⃗ \vec u u的计算表达式相同.
也就是每次空间到数轴的线性变换,都可以找到一个向量,称为该对象的对偶向量,使得应用线性变换(矩阵)与应用对偶向量点乘等价
8. 叉积的标准介绍
v ⃗ × w ⃗ \vec v \times \vec w v×w的计算结果是一个向量,两个向量所围成平行四边形的面积,如果 v ⃗ \vec v v在 w ⃗ \vec w w的右侧,所得结果为正

8.1 以线性变换的角度看待叉积
三维向量的叉积的计算方法如下:

叉积的理解与上面二维空间到一维数轴类似(点积)。叉积的理解需要定义一个三维到一维的线性变换,具体如下。

本质含义是找一个向量,使得它矩阵乘法(竖起来就是点积)的效果与它对应的矩阵线性变换效果相同。如果我们将右边的矩阵写出行列式的表达式,可以得出 三个问号 三个问号 三个问号的具体取值。行列式对应表达式的坐标就是 v ⃗ × w ⃗ \vec v \times \vec w v×w的坐标



9. 基变换
不同向量在不同坐标系下得到的坐标不同。比如 [ 1 , 3 ] [1,3] [1,3]是在 a a a坐标系下的, b b b坐标系可能就是 [ 3 , 5 ] [3,5] [3,5].那么在 a a a坐标系下的向量在 b b b坐标系下如何描述,这就是基变换。
我们可以先求得 a a a的基坐标在 b b b坐标的表示,再将 a a a的向量对应的拉伸长度与 a a a的基坐标在 b b b坐标系的表示相乘
下图中, [ 2 , 1 ] 与 [ − 1 , 1 ] [2,1]与[-1,1] [2,1]与[−1,1]是 a a a的基坐标在 b b b坐标系的表示, a a a中的向量

在 a a a坐标系下逆时针旋转90°,如何在 b b b坐标系下达到相同效果.取 b b b坐标系的任意一个向量,将它转化为 a a a坐标系下的向量表示,假设这个矩阵为 A A A.再乘上 a a a坐标系下逆时针旋转90°的旋转矩阵 M M M.最后转化回 B B B坐标系下,这个线性变换对应矩阵 A − 1 A^{-1} A−1.由上述可知 A M A − 1 AMA^{-1} AMA−1代表着一种转移作用,即 M M M代表的变换在其他坐标系的体现
10. 特征值与特征向量
教科书关于特征值与特征向量的定义:
A为n阶矩阵,若数λ和n维非0列向量x满足 A x = λ x Ax=λx Ax=λx,那么数λ称为A的特征值,x称为A的对应于特征值λ的特征向量。
它的几何意义是向量 X X X经过 A A A的线性变换后,长度拉伸而方向不变。
求解 A x = λ x − − − > ( A − λ I ) x = 0 Ax = λx---> (A- λI)x = 0 Ax=λx−−−>(A−λI)x=0 一个浅显的解是 X = 0 X = 0 X=0,但这没有什么意义。所以求解 B = A − λ I B =A- λI B=A−λI, B B B将二维空间压缩到了一维空间。只有压缩维度的情况存在,某一个非零向量才能在零空间里面,直接线性变换成零向量。这个非零向量是特征向量。
从三维角度来说,就是绕着特征向量旋转,并放大特征值倍。
顺带一提,二维线性变换特征向量有可能不存在,比如旋转90°的线性变换矩阵。
还有一个特征值,但特征向量不在一条直线上的情况。比如下面,这种情况下,所有向量都是特征向量
{ 2 0 0 2 } (1) \left\{ \begin{matrix} 2 & 0\\ 0 & 2\\ \end{matrix} \right\} \tag{1} {2002}(1)
如果特征向量刚好是基向量。这对应着对角矩阵,它的基向量都是特征向量。
特征基顾名思义,用特征向量作为基向量,构建坐标系;特征基矩阵可以理解为 用矩阵A的特征向量作为基向量,构建新的坐标系,在新的坐标系中表示A矩阵(变换),所得到的新矩阵,即特征基 矩阵 和 A矩阵 表示的是同一个变换,只不过他们是在不同坐标系中对同一个变换的不同描述而已, 并且特征基 矩阵 一定是对角阵。
这里简单说明一下原因,下面会有详细说明,无论是什么矩阵所表示的变换 对 矩阵的特征向量 都只有伸缩作用,不能改变方向,特征基 矩阵也不例外,恰好特征基矩阵的 特征向量正好也是基向量,那么可以这么说,特征基矩阵对其坐标系的每个维度的基向量只有缩放作用,所以其肯定是对角阵,或者我们用 I 表示特征基矩阵,那么I E 表示 I 矩阵对每个维度的基向量进行变换,有上述知I E为对角阵, 又由于E为单位阵 ,即I 为对角阵,即特征基矩阵一定为对角阵。
————————————————
版权声明:本文为CSDN博主「Lamar Davis」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/xiaoyink/article/details/101019929