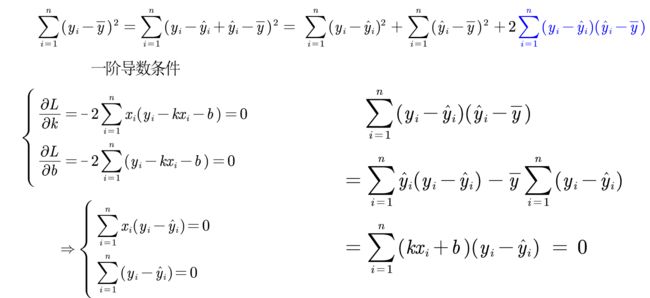清风数学建模学习笔记——拟合算法
拟合算法
与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所有的数据点最为接近,即曲线拟合的最好(最小化损失函数)。
文章目录
-
- 拟合算法
- 一、插值和拟合的区别
- 二、应用最小二乘法确定拟合曲线
- 三、评价拟合的好坏
- 四、扩展总结(★)
一、插值和拟合的区别
插值算法中,得到的多项式 f(x) 要经过所有样本点。但是如果样本点太多,那么这个多项式次数过高,会造成 龙格现象。尽管我们可以选择分段的方法避免这种现象,但是更多时候我们更倾向于得到一个确定的曲线,尽管这条曲线不能经过每一个样本点,但只要保证误差足够小即可,这就是拟合的思想。(拟合的结果是得到一个确定的曲线)
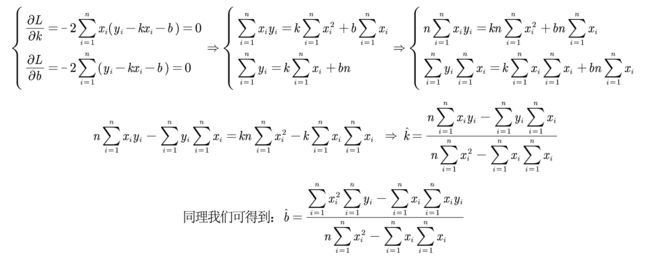
二、应用最小二乘法确定拟合曲线
问题提出:
设这些样本点 ( x i , y i ) , i = 1 , 2 , . . . , n (x_i, y_i), i=1,2,...,n (xi,yi),i=1,2,...,n,我们设置的拟合曲线为 y = k x + b y =kx + b y=kx+b,那么 当 k 和 b 取何值时,样本点和拟合曲线最接近?
第一种定义:
y i ^ = k x i + b , k ^ , b ^ = a r g m i n k , b ( ∑ i = 1 n ∣ y i − y i ^ ∣ ) \hat{y_i} =kx_i+b,\quad \hat{k},\hat{b}=\mathop{argmin}\limits_{k,b}(\sum_{i=1}^{n} |y_i-\hat{y_i}|) yi^=kxi+b,k^,b^=k,bargmin(i=1∑n∣yi−yi^∣)
第二种定义:
y i ^ = k x i + b , k ^ , b ^ = a r g m i n k , b ( ∑ i = 1 n ( y i − y i ^ ) 2 ) \hat{y_i} =kx_i+b,\quad \hat{k},\hat{b}=\mathop{argmin}\limits_{k,b}(\sum_{i=1}^{n} (y_i-\hat{y_i})^2) yi^=kxi+b,k^,b^=k,bargmin(i=1∑n(yi−yi^)2)
第一种定义有绝对值,不容易求导,因此计算比较复杂。所以我们往往使用第二种定义,这也正是最小二乘的思想。
问题:
- 为什么不用四次方?
(1)避免极端数据对拟合曲线的影响。
(2)最小二乘法得到的结果和MLE极大似然估计一致。 - 不用奇数次方的原因:误差会正负相抵。
三、评价拟合的好坏
用 拟合优度(可决系数) R 2 R^2 R2 拟合好坏的评价指标。
0 ≤ R 2 = S S R S S T = S S T − S S E S S T = 1 − S S E S S T ≤ 1 0 ≤ R^2=\frac{SSR}{SST}=\frac{SST-SSE}{SST}=1-\frac{SSE}{SST}≤1 0≤R2=SSTSSR=SSTSST−SSE=1−SSTSSE≤1
R 2 R^2 R2 越接近1,说明误差平方和越接近0,误差越小说明拟合的越好。
总 体 平 方 和 : S S T = ∑ i = 1 n ( y i − y ˉ ) 2 误 差 平 方 和 : S S E = ∑ i = 1 n ( y i − y ^ i ) 2 回 归 平 方 和 : S S R = ∑ i = 1 n ( y ^ i − y ˉ ) 2 总体平方和:SST=\sum_{i=1}^{n}(y_i - \bar{y})^2\\ 误差平方和:SSE=\sum_{i=1}^{n}(y_i - \hat{y}_i)^2\\ 回归平方和:SSR=\sum_{i=1}^{n}{(\hat{y}_i-\bar{y})^2} 总体平方和:SST=i=1∑n(yi−yˉ)2误差平方和:SSE=i=1∑n(yi−y^i)2回归平方和:SSR=i=1∑n(y^i−yˉ)2
证明SST = SSE + SSR:
R2 只能用于拟合函数是 “线性函数” 时,拟合结果的评价:
这里说的线性函数是指对 参数 为线性(线性于参数)。即在函数中,参数仅以一次方出现,且不能乘以或除以其他任何的参数,并不能出现参数的复合函数形式。
线性函数举例:
四、扩展总结(★)
- 拟合与插值算法的区别在于插值得到的函数经过所有样本点,而拟合得到的函数不一定经过所有样本点,但使得该曲线在某种准则下与所有的数据点最为接近。
- 在实际建模中,应用matlab中拟合工具箱进行拟合

- R 2 R^2 R2 只能用于拟合函数是 “线性函数”(参数线性) 时,拟合结果的评价。
本文借鉴了数学建模清风老师的课件与思路,如果大家发现文章中有不正确的地方,欢迎大家在评论区留言,也可以点击查看下方链接查看清风老师的视频讲解~
原文链接:https://www.bilibili.com/video/BV1DW411s7wi