图形学基础|基于LTC的面光源渲染

图形学基础|基于LTC的面光源渲染

一、前言

在之前实现的一些Demo中，直接光照部分，光源一直用的是精确的光源，即光源没有形状、面积大小等概念。

但实际上，光源并非是点光源这类精确的光源，而是有一定的形状、面积大小的AreaLight。

笔者也一直对AreaLight的渲染比较感兴趣。

本文将介绍并实现基于LTC（Linearly Transformed Cosines）的面光源渲染。

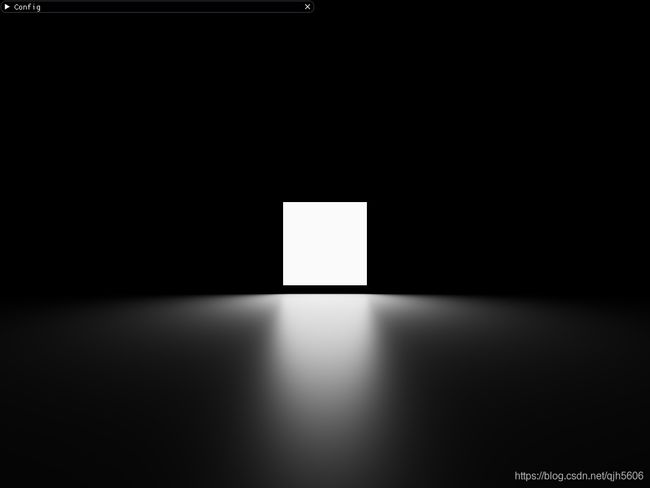
先给出笔者实现的效果图。

常量面光源：

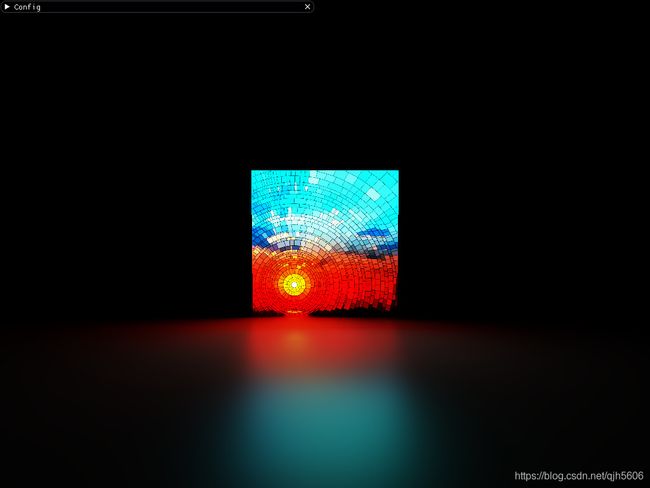
纹理面光源：

二、LTC（Linearly Transformed Cosines）

LTC（Linearly Transformed Cosines），线性变换余弦，这个概念出自论文《Real-Time Polygonal-Light Shading with Linearly Transformed Cosines》。

这篇论文解决的问题是：实时地实现多边形面光源的反射，并且能有基于物理的BRDF效果。

2.1 面光源

首先，我们来看一下面光源的光照计算公式：

$$I={\int }_{P}L(w_l)\rho (w_v,w_l)cos{\theta }_{l}d{w}_l$$

其中：

• $\rho$为BRDF函数；
• P为多边形；

为什么在实时渲染中，这个积分是有挑战性？

1. 在球面多边形上积分参数球面分布通常很困难；
2. State-of-the-art的PBR材质模型都不简单，即BRDF函数比较复杂，没有直接的解析解，采用蒙特卡洛方法求解积分则需要进行采样；

对于最常用的漫反射BRDF（Lambertian )，即$\rho =\frac{albedo}{\pi }$，且光源各处强度恒定即$L=L(w_l)$，则积分为：

$$I=\rho L{\int }_{P}cos{\theta }_{l}d{w}_l$$

这个积分是有解析解的！

详细的算法参考Geometric Derivation of the Irradiance of Polygonal Lights，本文后续也会进行介绍。

这个结论会在论文后续的积分求解中被使用！非常重要！

2.2 线性变化球形分布

为了求解上面所提到的积分式，论文的作者引入了一种线性变换球面分布Linearly Transformed Spherical Distributions（LTSDs） 的思想。

即对是对于任意一个球面分布函数，一定可以通过一个3X3的线性变换矩阵将其变化到另外一个球面分布函数。

经过这个线性变换后，改变了原分布的”形状“。

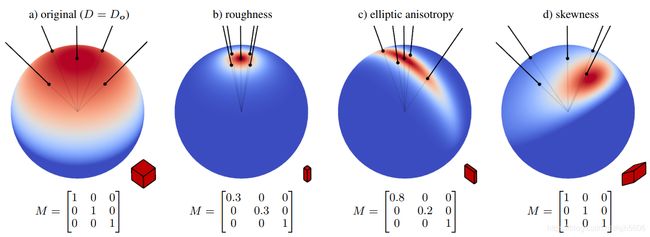
如下图所示：

• 对原始球面分布的方向向量，应用不同的线性变换矩阵，修改了原始分布的形状。

不同的原始分布，能够创建具有不同形状的参数分布。

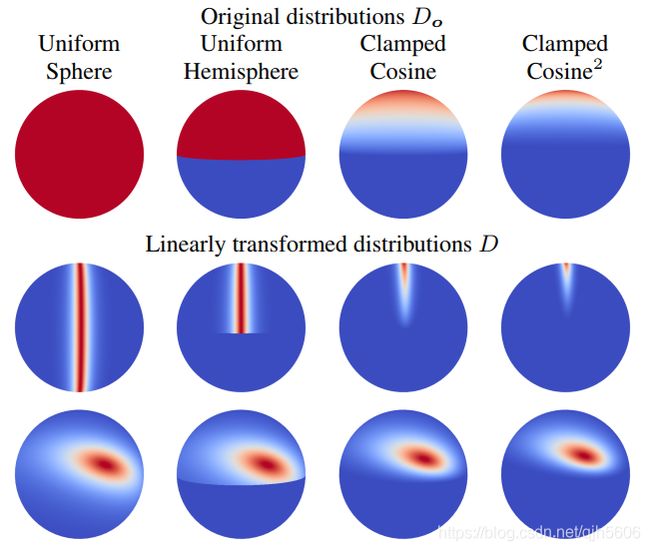
下图展示了4种不同的原始分布，以及其应用线性变换矩阵后产生的分布形状。

• 原始分布这里有：球面均匀分布、半球均匀分布、截断余弦、截断余弦平方。

经过线性变换后的分布，新的球面分布继承了原分布的一些特点，例如归一化，球面多边形积分，重要性采样等。

问题：为什么要引入这个线性变换呢？

我们的目标始终是求解上面所提到的积分式：$I={\int }_{P}L(w_l)\rho (w_v,w_l)cos{\theta }_{l}d{w}_l$。

由于BRDF比较复杂，但其实它也是球面上的一种分布。

基于线性变化球形分布，我们是否能够找到一个线性变换矩阵将无法求解的$\rho (w_v,w_l)cos{\theta }_l$分布，转换为比较容易求解积分的分布呢？

这就是为什么引入这样的线性变化球形分布。

下面将对此进行详细地介绍说明。

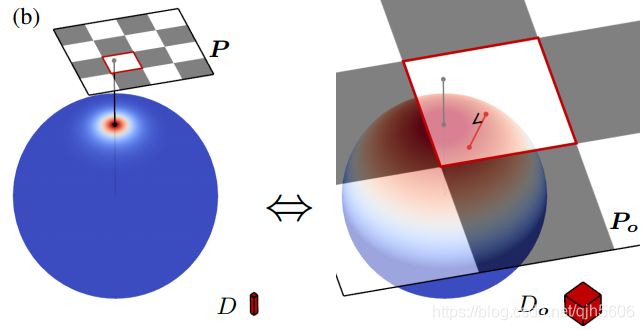
2.2.1 定义

Original Distribution to be Transformed（变换原始分布）

$D_0$是原始分布，D是新的球面分布。

通过应用一个$3\times 3$的线性变换矩阵，将原始分布变换成为新的分布。

具体的变换公式如下：

$$\omega =M{\omega }_o/||M{\omega }_o||$$

逆变换为：

$${\omega }_o=M^{-1}\omega /||M^{-1}\omega ||$$

这两个分布具有以下的关系式：

$$D(\omega )=D({\omega }_o)\frac{\partial {\omega }_o}{\partial \omega }$$

其中，$\frac{\partial {\omega }_o}{\partial \omega }=（\frac{M^{-1}\omega }{||M^{-1}||\omega }）\frac{|M^{-1}|}{||M^{-1}\omega |{|}^3}$。

当$M$为旋转或缩放矩阵时，以此它是不会改变分布的形状的，此时 $\frac{\partial {\omega }_o}{\partial \omega }=1$。

2.2.2 性质

变换后的分布$D$继承了若干原有分布$D_o$的特性。

Normalization（归一化）

$${\int }_{\Omega }D(\omega )d\omega ={\int }_{\Omega }{D}_o({\omega }_o)\frac{\partial {\omega }_o}{\partial \omega }d\omega ={\int }_{\Omega }{D}_o({\omega }_o)d{\omega }_o$$

• 这个公式的推导仅仅把上面的微分公式带入即可。

Integration over Polygons（多边形上积分）

$${\int }_{P}D(\omega )d\omega ={\int }_{P_o}D({\omega }_o)d{\omega }_0$$

其中，$P_o=M^{-1}P$。

即有：

• 变换后的分布$D$在多边形$P$上进行积分，等效于原始分布$D_o$中在多边形$P_o$上进行积分。

根据方程含义进行解释，左侧所求积分的意思是：$D$采样的方向和多边形$P$相交的概率。

所以，任何线性变换作用在$D$的方向向量和多边形$P$并不会改变相交（intersections），因此积分值不变。

如下图所示：

2.3 以LTC拟合BRDF

由2.2可知，可以通过一个$3\times 3$的线性变换矩阵$M$的逆矩阵，可以将复杂难以求解某种球面分布上对多边形的积分转为比较容易求解的形式。

那么如何选择原始分布$D_o$呢？

作者选择了：半球上的归一化clamped cosine distribution（截断余弦分布）。

$$D_o({\omega }_o=(x,y,z))=\frac{1}{\pi }max(0,z)$$

将$D_o$带入公式，$D(\omega )=D({\omega }_o)\frac{\partial {\omega }_o}{\partial \omega }$，即可得到线性变换余弦LTC，即$D(\omega )$。

那么，接下来一个问题是：线性变换矩阵$M$应该要如何求解呢？

选择去近似GGX微表面BRDF（菲涅尔项为1），更准备地说要近似的是余弦加权的BRDF：

$$D\approx \rho ({\omega }_v,{\omega }_l)cos{\theta }_l$$

对于各项同性的材质，BRDF依赖于入射方向$(sin{\theta }_v,0,cos{\theta }_v)$和粗糙度$\alpha$。

• 注，这里坐标是作为切线空间的坐标。
• 切线空间是法线$N$为$Z$方向的局部坐标系。

对于任意组合$({\theta }_v,\alpha )$，使用LTC进行拟合余弦加权的BRDF，即每个组合找到一个$M$矩阵，使得足够接近。

由于各向同性BRDF的平面对称性，并且由于线性变换余弦是尺度不变的。

最终矩阵$M$的表示形式如下：

$$M=\left[\begin{array}{ccc}a& 0& b\\ 0& c& 0\\ d& 0& 1\end{array}\right]$$

在实践中发现，该形式的矩阵，a、b、c、d随着$（\theta ,\alpha ）$的变化不平缓。

因而最终采用了如下实现的矩阵M：

$$M=\left[\begin{array}{ccc}a& 0& b\\ 0& 1& 0\\ c& 0& d\end{array}\right]$$

仅需要拟合4个参数。

同时，作者根据经验，发现最小化L3错误会在着色方面产生最佳视觉效果。

这样拟合过程，只用考虑 4 个变量。拟合所得矩阵$M$的逆（同样只有四个参数，在渲染过程中只需要逆矩阵）可以存储在一个2D贴图LUT的四个通道中。

拟合的过程大概如下：

作者提供了拟合BRDF的源代码ltc_code/fit/。

在具体的拟合过程中，M矩阵是没有考虑菲涅尔项的（假定其为1）。

因为菲涅耳项包含了一个与材质固有属性相关的F0项，即0度角入射的菲涅尔反射率。

LTC Fresnel Approximation给出了含Fresnel的BRDF，公式如下：

$$\begin{array}{rl}n& ={\int }_{\Omega }F({\omega }_v,{\omega }_l)\rho ({\omega }_v,{\omega }_l)cos{\theta }_{l}d{\omega }_l\\ & ={\int }_{\Omega }[F_0+(1-F_0)(1-{⟨{\omega }_l,{\omega }_h⟩}^5)]\rho ({\omega }_v,{\omega }_l)cos{\theta }_{l}d{\omega }_l\\ & =F_0{\int }_{\Omega }\rho ({\omega }_v,{\omega }_l)cos{\theta }_{l}d{\omega }_l(1-F_0){\int }_{\Omega }(1-{⟨{\omega }_l,{\omega }_h⟩}^5)\rho ({\omega }_v,{\omega }_l)cos{\theta }_{l}d{\omega }_l\\ & =F_0{n}_D+(1-F_0)f_D\end{array}$$

将 $n_D$和$f_D$进行预计算存储，这和PBR回顾中的BRDF-LUT没有什么不同。

拟合的具体处理如下：

1. 在出射角度方向为$\theta$，粗糙度为$\alpha$的情况下，估计对应的reflectance和入射光方向；

对应的代码如下：

// 计算BRDF（不包含菲涅尔系数）项与菲涅尔系数项与重要性采样大致方向（用于获得一个初始单纯形）
void computeAvgTerms(const Brdf& brdf, const vec3& V, const float alpha,
	float& norm, float& fresnel, vec3& averageDir)
{
	norm = 0.0f;
	fresnel = 0.0f;
	averageDir = vec3(0, 0, 0);

	for (int j = 0; j < Nsample; ++j)
		for (int i = 0; i < Nsample; ++i)
		{
			const float U1 = (i + 0.5f) / Nsample;
			const float U2 = (j + 0.5f) / Nsample;

			// sample
			// 采样到一个方向
			const vec3 L = brdf.sample(V, alpha, U1, U2);

			// eval
			// 计算BRDF（不含菲尼尔系数项）* dot(N,L)方程值，并得到其概率密度函数pdf
			float pdf;
			float eval = brdf.eval(V, L, alpha, pdf);

			if (pdf > 0)
			{ 
				// 计算权重（重要性采样）
				float weight = eval / pdf;

				vec3 H = normalize(V + L);

				// accumulate
				//norm存储的是论文Fresnel项附加材料中的nD
				norm += weight;	
				//fresnel存储的是论文Fresnel项附加材料中的fD
				fresnel += weight * pow(1.0f - glm::max(dot(V, H), 0.0f), 5.0f);
				// 计算重要性采样的大致方向
				averageDir += weight * L;
			}
		}

	norm /= (float)(Nsample * Nsample);
	fresnel /= (float)(Nsample * Nsample);

	// clear y component, which should be zero with isotropic BRDFs
	// 各向同性，不考虑方位角
	averageDir.y = 0.0f;
	// 归一化重要性采样的平均方向
	averageDir = normalize(averageDir);
}

采样方向的函数sample如下：

virtual vec3 sample(const vec3& V, const float alpha, const float U1, const float U2) const
{
    // 计算方位角
    const float phi = 2.0f * 3.14159f * U1;
    // 修正粗糙度
    const float r = alpha * sqrtf(U2 / (1.0f - U2));
    // 通过枚举法线方向而不是观察方向得到所有法线与观察向量的组合情况
    const vec3 N = normalize(vec3(r * cosf(phi), r * sinf(phi), 1.0f));
    // 通过公式计算反射向量即入射光方向
    const vec3 L = -V + 2.0f * N * dot(N, V);
    return L;
}

计算BRDF值的函数eval如下：

virtual float eval(const vec3& V, const vec3& L, const float alpha, float& pdf) const
{
    // 位于上半球之下，返回0
    if (V.z <= 0)
    {
        pdf = 0;
        return 0;
    }

    // masking
    const float LambdaV = lambda(alpha, V.z);

    // shadowing
    float G2;
    if (L.z <= 0.0f)
        G2 = 0;
    else
    {
        const float LambdaL = lambda(alpha, L.z);
        G2 = 1.0f/(1.0f + LambdaV + LambdaL);
    }

    // D
    // 法线分布函数部分
    const vec3 H = normalize(V + L);
    const float slopex = H.x / H.z;
    const float slopey = H.y / H.z;
    // 这个slopex* slopex + slopey * slopey其实等于(x ^ 2 + y ^ 2) / z ^ 2，结果就是tan(theta) * tan(theta)
    float D = 1.0f / (1.0f + (slopex * slopex + slopey * slopey) / alpha / alpha);
    D = D * D;
    D = D / (3.14159f * alpha * alpha * H.z * H.z * H.z * H.z);

    // 概率密度函数
    // GGX重要性采样得到的H向量的话：
    // 概率密度函数PDF为：D* NoH
    // 采样的是L向量的话：
    // PDF需要根据雅可比行列式进行转换，将H的分布概率转换为L的概率分布
    pdf = fabsf(D * H.z / 4.0f / dot(V, H));

    // Result = BRDF * dot(N,L) = DFG / (4 * dot(N,L) * dot(N,V)) * dot(N, L)
    // Result = BRDF * dot(N,L) = DFG / (4 * dot(N,V)) 
    // F = 1，dot(N,V) = V.z
    // Result = BRDF * dot(N,L) = DG / (4 * V.z) 
    float res = D * G2 / 4.0f / V.z;
    return res;
}

注：

这里使用的D法线分布函数部分，计算方法有点不同于平时看到的公式。

笔者曾用UE4的D_GGX进行替换发现计算过程会出现nan值。

2. 通过Nelder–Mead Simplex单纯形法不断修正M矩阵使积分结果无限近似BRDF。

单行法的算法详情查看Nelder–Mead Simplex

代码如下：

// fit brute force
// refine first guess by exploring parameter space
void fit(LTC& ltc, const Brdf& brdf, const vec3& V, const float alpha, const float epsilon = 0.05f, const bool isotropic = false)
{
	float startFit[3] = { ltc.m11, ltc.m22, ltc.m13 };
	float resultFit[3];

	FitLTC fitter(ltc, brdf, isotropic, V, alpha);

	// Find best-fit LTC lobe (scale, alphax, alphay)
    // 通过NelderMead单纯形算法，计算误差得到最终的M矩阵
	float error = NelderMead<3>(resultFit, startFit, epsilon, 1e-5f, 100, fitter);

	// Update LTC with best fitting values
	fitter.update(resultFit);
}

具体的NelderMead代码就不贴了。

最后，程序将拟合完的结果存储为两张贴图，分别为ltc_1.dds和ltc_2.dds。

• ltc_1中4个通道分别存储了逆矩阵M中的a、b、c、d系数。

const mat3& m = tab[i];
mat3 invM = inverse(m);
// normalize by the middle element，除了矩阵的中间元素，可以少存一个元素（从5个变成4个）
invM /= invM[1][1];
// store the variable terms
tex1[i].x = invM[0][0];
tex1[i].y = invM[0][2];
tex1[i].z = invM[2][0];
tex1[i].w = invM[2][2];

• ltc_2中的R通道存储了$n_D$，G通道存储了$f_D$。

三、使用LTC进行多边形光源着色

3.1 Shading with Constant Polygonal Lights

Constant Polygonal Lights， 即多边形光源各个地方的强度为恒定的值，$L({\omega }_l)=L$ 。

因此，所求的积分就变成：

$$\begin{array}{rl}I& ={\int }_{P}L({\omega }_l)D({\omega }_l)d{\omega }_l\\ & =L{\int }_{P}D({\omega }_l)d{\omega }_l\\ & =L{\int }_{P_o}{D}_o({\omega }_o)d{\omega }_o\\ & =L\ast E(P_o)\end{array}$$

E是多边形$P_o$的Irradiance。由于$Do$是clamped cosine distribution，这积分是有封闭形式的解析表示式：

$$E(p_1,\cdots ,p_n)=\frac{1}{2\pi }\sum _{i=1}^{n}acos(⟨p_i,p_j⟩)⟨\frac{p_i\times p_j}{\Vert P_i\times p_j\Vert },\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]⟩$$

其中，$p_i,p_j$表示多边形的顶点。j = (i mod n) + 1。

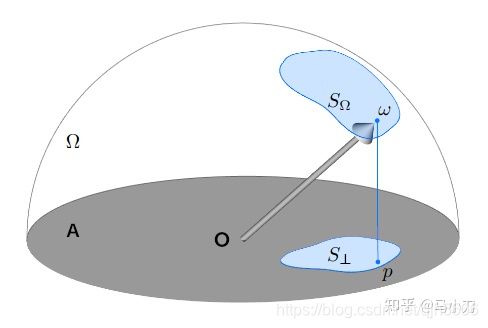
要求解的多边形的辐射照度E，等于多边形的投影面积$S_{\perp }$除以$\pi$。

所以，如何求解半球面上的多边形$S_{\Omega }$在水平面的投影面积$S_{\perp }$呢？

这可以从计算任意平面多边形的面积讲起，再扩展到半球面。

平面多边形的面积公式为：

$$S_{p_1,p_2...p_n}=\frac{1}{2}\sum _{i=1}^n(O{P}_i\times O{P}_j)$$

其中，O为原点。

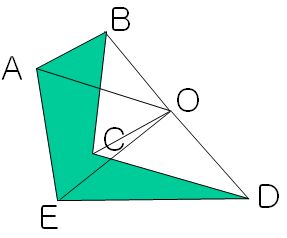
将多边形的面积拆解成为一个个三角形的面积叠加求解。

而对于半球面上的多边形在水平面上的投影面积，可以拆解为一个个扇形投影到水平面。

对于半球面上的一个扇形$O{P}_i{P}_j$，其面积为：$S=\frac{1}{2}\theta r^2$，由于这里的单位半球，$r=1$，

则只需要求解角度$\theta$，通过余弦定理有：

$$\theta =arccos(O{P}_i,O{P}_j)$$

那么扇形投影到水平面为：

$S_{\perp }=Scos\varphi$

这里，$\varphi$为扇形$O{P}_i{P}_j$法线与水平面法线的夹角。

扇形$O{P}_i{P}_j$法线可以通过平面上两向量叉乘得到，即：

$$O{P}_i\times O{P}_j$$

水平面的法线为：$n=(0,0,1)$。

则余弦值为：

$$cos\varphi =\frac{O{P}_i\times O{P}_j}{||O{P}_i\times O{P}_j||}\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$

将n个扇形的投影进行叠加，则得到了所要的半球面上的多边形在水平面的投影面积。

$$S_{\perp }(p_1,\cdots ,p_n)=\frac{1}{2}\sum _{i=1}^{n}acos(⟨p_i,p_j⟩)⟨\frac{p_i\times p_j}{\Vert P_i\times p_j\Vert },\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]⟩$$

投影面积除以π，得到多边形的辐射照度，即完成了上述公式E的推导。

3.2 Shading with Textured Polygonal Lights

假设光源发射的Radiance可以用一张2D颜色纹理进行表示，在这种情况不能像上述以常量近似而进行分离。

将公式改写为：

$$\begin{array}{rl}A& \approx {\int }_{P}L(w_l)D(w_l)d{w}_l=I_D{I}_L\\ I_D& ={\int }_{P}D(w_l)d{w}_l\\ I_L& =\frac{{\int }_{P}L(w_l)D(w_l)d{w}_l}{{\int }_{P}D(w_l)d{w}_l}\end{array}$$

通过裂项将问题拆解为：

• The Shape of the Highlight（高光的形状） $I_D$
• The Color of the Highlight（高光的颜色） $I_L$

其中，$I_D$就是3.1求解的E。

那么如何求解$I_L$项呢？

作者是这么表述的：

• 可以被看成$D$中与$P$相交的光线聚集的平均颜色，負責高光的颜色。

• 可以被表述为一个纹理空间的过滤器（texture-space filter）!!!

使用预过滤的纹理来近似，看做纹理L通过一个过滤器：

$$F(w_l)=\frac{D(w_l)}{{\int }_{P}D(w_l)d{w}_l}$$

感叹作者的思路真的太强了！ORZ

四、渲染

通过上面的介绍，我们得到了通过LTC方法渲染多边形光源的方案，实时渲染的流程如下：

1. 采样 LUT 得变换矩阵；

2. 将面光源的各个顶点变换一下；

3. 裁剪变换后的多边形（变成三角形、长方形或五边形）；

4. 利用clamped cosine distribution的解析解直接求出积分值；

5. 采样菲涅尔项调整4的结果；

4.1 采样LTC

根据粗糙度和View向量和法向量的点乘结果，查询LTC1纹理构造矩阵：

const static float LUT_SIZE = 64.0;
const static float LUT_SCALE = (LUT_SIZE - 1.0) / LUT_SIZE;
const static float LUT_BIAS = 0.5 / LUT_SIZE;

float2 LTC_Coords(float Roughness, float CosTheta)
{
	float2 Coords = float2(Roughness, sqrt(1 - CosTheta));
	// scale and bias coordinates, for correct filtered lookup
	Coords = Coords * LUT_SCALE + LUT_BIAS;
	return Coords;
}

float NoV = saturate(dot(Normal, ViewDir));
// 计算UV计算
float2 UV = LTC_Coords(Roughness, NoV);

// 采样LTC1
float4 t1 = LTC_MatrixTexture.SampleLevel(LinearSampler, UV, 0);

float3x3 Minv = float3x3
    (
    float3(t1.x, 0, t1.y),
    float3(0, 1, 0),
    float3(t1.z, 0, t1.w)
);

再利用这个矩阵对多边形进行旋转！

注，这个旋转是在切线空间定义的，所以要先经多边形的顶点变换到切线空间。

代码如下：

// Orthogonal basis of tangent space on shading point
float3 Tangent = normalize(ViewDir - Normal * dot(ViewDir, Normal));
float3 Bitangent = cross(Tangent, Normal);
// 构造TBN矩阵
float3x3 TBN = float3x3(Tangent, Bitangent, Normal);
// 求逆矩阵
TBN = transpose(TBN);

float3 L[5];
// 将多边形先变换到切线空间
L[0] = mul((Points[0] - PixelWorldPos), TBN);
L[1] = mul((Points[1] - PixelWorldPos), TBN);
L[2] = mul((Points[2] - PixelWorldPos), TBN);
L[3] = mul((Points[3] - PixelWorldPos), TBN);
// 再进行Minv的变换
L[0] = mul(L[0], Minv);
L[1] = mul(L[1], Minv);
L[2] = mul(L[2], Minv);
L[3] = mul(L[3], Minv);
L[4] = L[0];

4.2 裁剪

经过Minv矩阵的变换后，四边形可能出现部分落在下半球，需要进行裁剪。

裁剪后可能变成3边形，4边形或5边形。

裁剪的代码如下：

void ClipQuadToHorizon(inout float3 L[5], inout int n)
{
	// detect clipping config
	int config = 0;
	if (L[0].z > 0.0) config += 1;
	if (L[1].z > 0.0) config += 2;
	if (L[2].z > 0.0) config += 4;
	if (L[3].z > 0.0) config += 8;

	// clip
	n = 0;

	if (config == 0)
	{
		// clip all
	}
	else if (config == 1) // V1 clip V2 V3 V4
	{
		n = 3;
		L[1] = -L[1].z * L[0] + L[0].z * L[1];
		L[2] = -L[3].z * L[0] + L[0].z * L[3];
	}
	else if (config == 2) // V2 clip V1 V3 V4
	{
		n = 3;
		L[0] = -L[0].z * L[1] + L[1].z * L[0];
		L[2] = -L[2].z * L[1] + L[1].z * L[2];
	}
	else if (config == 3) // V1 V2 clip V3 V4
	{
		n = 4;
		L[2] = -L[2].z * L[1] + L[1].z * L[2];
		L[3] = -L[3].z * L[0] + L[0].z * L[3];
	}
	else if (config == 4) // V3 clip V1 V2 V4
	{
		n = 3;
		L[0] = -L[3].z * L[2] + L[2].z * L[3];
		L[1] = -L[1].z * L[2] + L[2].z * L[1];
	}
	else if (config == 5) // V1 V3 clip V2 V4) impossible
	{
		n = 0;
	}
	else if (config == 6) // V2 V3 clip V1 V4
	{
		n = 4;
		L[0] = -L[0].z * L[1] + L[1].z * L[0];
		L[3] = -L[3].z * L[2] + L[2].z * L[3];
	}
	else if (config == 7) // V1 V2 V3 clip V4
	{
		n = 5;
		L[4] = -L[3].z * L[0] + L[0].z * L[3];
		L[3] = -L[3].z * L[2] + L[2].z * L[3];
	}
	else if (config == 8) // V4 clip V1 V2 V3
	{
		n = 3;
		L[0] = -L[0].z * L[3] + L[3].z * L[0];
		L[1] = -L[2].z * L[3] + L[3].z * L[2];
		L[2] = L[3];
	}
	else if (config == 9) // V1 V4 clip V2 V3
	{
		n = 4;
		L[1] = -L[1].z * L[0] + L[0].z * L[1];
		L[2] = -L[2].z * L[3] + L[3].z * L[2];
	}
	else if (config == 10) // V2 V4 clip V1 V3) impossible
	{
		n = 0;
	}
	else if (config == 11) // V1 V2 V4 clip V3
	{
		n = 5;
		L[4] = L[3];
		L[3] = -L[2].z * L[3] + L[3].z * L[2];
		L[2] = -L[2].z * L[1] + L[1].z * L[2];
	}
	else if (config == 12) // V3 V4 clip V1 V2
	{
		n = 4;
		L[1] = -L[1].z * L[2] + L[2].z * L[1];
		L[0] = -L[0].z * L[3] + L[3].z * L[0];
	}
	else if (config == 13) // V1 V3 V4 clip V2
	{
		n = 5;
		L[4] = L[3];
		L[3] = L[2];
		L[2] = -L[1].z * L[2] + L[2].z * L[1];
		L[1] = -L[1].z * L[0] + L[0].z * L[1];
	}
	else if (config == 14) // V2 V3 V4 clip V1
	{
		n = 5;
		L[4] = -L[0].z * L[3] + L[3].z * L[0];
		L[0] = -L[0].z * L[1] + L[1].z * L[0];
	}
	else if (config == 15) // V1 V2 V3 V4
	{
		n = 4;
	}

	if (n == 3)
		L[3] = L[0];
	if (n == 4)
		L[4] = L[0];
}

4.3 线积分

对裁剪之后边进行线积分，求出解析解。

L[0] = normalize(L[0]);
L[1] = normalize(L[1]);
L[2] = normalize(L[2]);
L[3] = normalize(L[3]);
L[4] = normalize(L[4]);

float3 VSum = float3(0, 0, 0);
VSum += IntegrateEdgeVec(L[0], L[1]);
VSum += IntegrateEdgeVec(L[1], L[2]);
VSum += IntegrateEdgeVec(L[2], L[3]);

if (VertexNum >= 4)
    VSum += IntegrateEdgeVec(L[3], L[4]);
if (VertexNum == 5)
    VSum += IntegrateEdgeVec(L[4], L[0]);

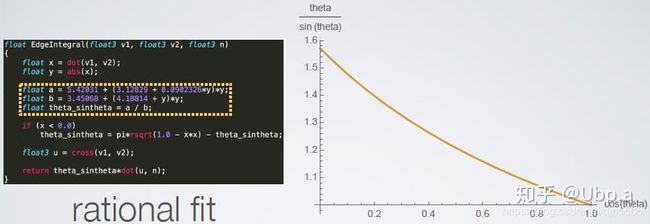
IntegrateEdgeVec函数采用了拟合的方式直接得到 $theta/sin\theta$。

笔者直接采用了selfshadow/ltc_code中的积分代码：

float inversesqrt(float f)
{
	return 1.0f / sqrt(f);
}

float3 IntegrateEdgeVec(float3 v1, float3 v2)
{
	float x = dot(v1, v2);
	float y = abs(x);

	float a = 0.8543985 + (0.4965155 + 0.0145206 * y) * y;
	float b = 3.4175940 + (4.1616724 + y) * y;
	float v = a / b;

	float theta_sintheta = (x > 0.0) ? v : 0.5 * inversesqrt(max(1.0 - x * x, 1e-7)) - v;
	float3 l = cross(v1, v2);
	return l * theta_sintheta;
}

4.4 纹理过滤与采样

纹理过滤这块笔者没有自己实现。

使用了【论文复现】Real-Time Polygonal-Light Shading with LinearlyTransformed Cosines中的资源。

将其拼成一张TextureArray.dds。

• 光源纹理，提取码: gw32。

一次纹理fetch需要两个量：

• UV坐标；
• LOD级别（这里应该是TextureArray的Index）；

在变换后的余弦空间，采用正交投影orthonormal projection，将着色点投影到纹理平面，计算UV坐标。

LOD的选择简化为到纹理平面的平方距离r2与多边形面积A之间比率的一维函数。

具体的代码如下：

float3 FetchDiffuseFilteredTexture(float3 L[5])
{
	float3 V1 = L[1] - L[0];
	float3 V2 = L[3] - L[0];
	// Plane's normal
	float3 PlaneOrtho = cross(V1, V2);
	float PlaneAreaSquared = dot(PlaneOrtho, PlaneOrtho);
	float planeDistxPlaneArea = dot(PlaneOrtho, L[0]);
	// orthonormal projection of (0,0,0) in area light space
	float3 P = planeDistxPlaneArea * PlaneOrtho / PlaneAreaSquared - L[0];

	// find tex coords of P
	float dot_V1_V2 = dot(V1, V2);
	float inv_dot_V1_V1 = 1.0 / dot(V1, V1);
	float3 V2_ = V2 - V1 * dot_V1_V2 * inv_dot_V1_V1;
	float2 UV;
	UV.y = dot(V2_, P) / dot(V2_, V2_);
	UV.x = dot(V1, P) * inv_dot_V1_V1 - dot_V1_V2 * inv_dot_V1_V1 * UV.y;

	// LOD
	float d = abs(planeDistxPlaneArea) / pow(PlaneAreaSquared, 0.75);
	float Lod = log(2048.0 * d) / log(3.0);
	float LodA = floor(Lod);
	float LodB = ceil(Lod);
	float t = Lod - LodA;
	float3 ColorA = FilteredLightTexture.Sample(LinearSampler, float3(UV, LodA)).rgb;
	float3 ColorB = FilteredLightTexture.Sample(LinearSampler, float3(UV, LodB)).rgb;
	return lerp(ColorA, ColorB, t);
}

参考博文

• 《Real-Time Polygonal-Light Shading with Linearly Transformed Cosines》
• selfshadow/ltc_code
• Real-Time Polygonal-Light with LTC
• 【论文复现】Real-Time Polygonal-Light Shading with LinearlyTransformed Cosines
• 面光源的渲染
• 利用LTC实现实时多边形面积光
• 线性变换余弦算法