图形学基础|深度缓冲（DepthBuffer）

图形学基础|深度缓冲（DepthBuffer）

一、前言

在实时渲染中，深度缓冲（Depth Buffer） 扮演着非常重要的角色。

通常，深度缓冲区记录着屏幕对应的每个像素的深度值。

通过深度缓冲区，可以进行深度测试，从而确定像素的遮挡关系，保证渲染正确。这是深度缓冲最主要的作用。

不过，知道深度缓冲的作用和深入理解深度还存在一定的距离，本文将对深度进行一个更加细致的介绍，包含了非线性深度和线性深度，Reverse-Z，以及如何根据深度重建世界坐标。

在更多的图形算法中，对深度的使用过程中一定会涉及到这些基础的知识，只有充分的理解和掌握这些内容，才能更快地理解和实现图形算法。

二、线性深度与非线性深度

2.1 线性深度

所谓线性，就是指变化曲线的一阶导数为常量。例如：$F(z)=z$。

在相机Camera空间（观察View空间），深度$z$就是线性的，$z$可能是投影平截头体的近平面（Near）和远平面（Far）之间的任何值。

但完整地记录这个确定的值是比较浪费的，因此可以通过一种方式可以将其转换到$[0,1]$区间：

$$F_{Depth}=\frac{z-near}{far-near}$$

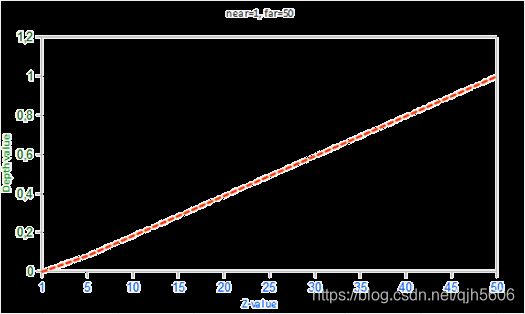
这里的$near$和$far$值是我们之前提供给投影矩阵设置可视平截头体的近平面（near plane）和远平面（far plane），可以看出来，这个方程计算得到的深度值仍然是线性的。

下图提供了一个示例，展示了$z$值和对应的深度值之间的关系。

2.2 非线性深度

$3D$图形渲染最终的目标是将三维空间的空间点投影到二维的平面上，所以在相机空间之后，还需要通过投影将坐标由Camera空间变换到Clip空间。

注，Clip Space并不等于NDC空间。通过透视除法才从ClipSpace变换到了NDC空间。

下图清晰地展示了一个顶点从相机空间到到视平面的坐标变化过程。包含了投影变换，透视除法，视口变换。

上述的NDC空间为D3D的。对于OpenGL，其NDC空间中，$z$的取值范围为$[-1,1]$。

一般而言，投影采用的矩阵为透视矩阵。投影矩阵的推导以下的文章：

OpenGL Projection Matrix

图形学基础之透视校正插值

Direct3D - 透视投影矩阵与齐次裁剪空间

经过投影矩阵的变化后，线性深度$z$将会被映射成为深度$d$。

在D3D中，z会被规范到$[0,1]$，令$g(z)$为映射函数，有：

$$\begin{array}{c}g(z)=A+\frac{B}{z}\\ 0\le g(z)\le 1\\ n\le z\le f\end{array}$$

将$z=n$和$z=f$带入，有：

$$\begin{array}{cc}A+\frac{B}{n}& =0\\ A+\frac{B}{f}& =1\end{array}$$

解的：

$$\begin{array}{cc}A& =\frac{f}{f-n}\\ B& =-\frac{nf}{f-n}\end{array}$$

则$g(z)$的表达式如下：

$$g(z)=\frac{f}{f-n}-\frac{nf}{(f-n)z}$$

这就是通常（不考虑Reverse-Z）D3D中，Depth Buffer中存储的值。

而OpenGL中Depth Buffer只是将NDC的z从[-1,1]线性映射到了[0,1]而已。

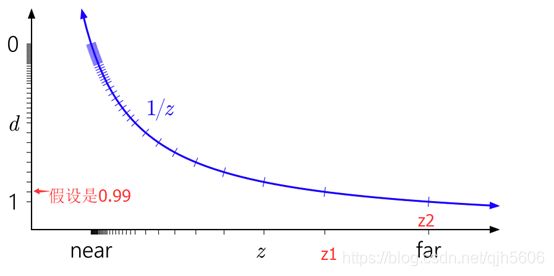
非线性方程与 1/z 成正比。

从图中，我们可以看到距离摄像机很近的地方，占据了大半的深度取值范围。离摄像机越远的物体，信息就越少，对画面的贡献也越少，根本不需要为远处物体的数据提供更高的精度。

2.3 深度可视化

屏幕空间中的深度值$d$是非线性的，可视化深度的话需要将DepthBuffer中的深度进行线性化，再进行显示。

需要处理了D3D和OpenGL平台差异性，将D3D的$[0,1]$非线性空间和OpenGL的$[0,1]$非线性空间都计算到了$[0,1]$的线性空间。

对于OpenGL：

float LinearizeDepth(float depth) 
{
    float z = depth * 2.0 - 1.0; // back to NDC 
    return (2.0 * near * far) / (far + near - z * (far - near));    
}

对于D3D：

float LinearizeDepth(float depth) 
{
    float z = depth;
    return (near * far) / (far - z * (far - near));    
}

可视化的效果如图：

三、深度测试

在绘制3D场景的时候，我们需要决定哪些部分对观察者是可见的，或者说哪些部分对观察者不可见。

对于不可见的部分，我们应该及早地丢弃，例如在一个不透明的墙壁后的物体就不应该渲染。

早期的实现方法通过画家算法进行隐藏面消除，先绘制场景中离观察者较远的物体，再绘制较近的物体。

但是这种方法无法解决物体存在互相重叠的情况如下图。

因而，出现了像素级别的深度缓冲方法：通过和颜色缓冲（Color Buffer）一样分辨率的缓冲存储深度信息，从而实现可见性的判断。它会以16、24或32位float的形式储存它的深度值。在大部分的系统中，深度缓冲的精度都是24位的。

3.1 Early-Z

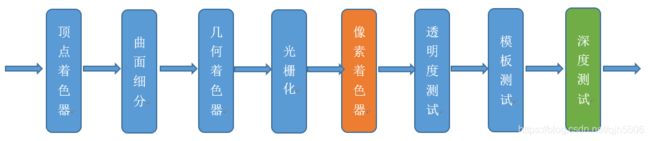
在传统的渲染管线中，深度测试是发生在Pixel/Fragment Shader之后的，这样的效率是比较低的，会造成大量的无用计算。

现在大部分的GPU都提供一个叫做提前深度测试（Early Depth Testing）的硬件特性，称为Early-Z。

Early-Z指的是：在Vertex阶段和Fragment阶段之间（光栅化之后，fragment之前）进行一次深度测试。

如果深度测试失败，就不必进行fragment阶段的计算了，因此在性能上会有很大的提升。但是最终的ZTest仍然需要进行，以保证最终的遮挡关系结果正确。

提前进行深度测试可以节省不必要像素的片元计算，所以会有性能的提升。

Intel - Early Z Rejection文章中还展示了两种方式实现early-z，一种是通过从前向后渲染，另外一种通过Pre-Z-Pass实现。

This sample demonstrates two ways to take advantage of early Z rejection. When rendering, if the hardware detects that after performing vertex shading a fragment will fail the depth test, it can avoid the cost of executing the pixel shader and reject the fragment. To best take advantage of this feature, it is necessary to maximize the number of fragments that can be rejected because of depth testing. This sample demonstrates two ways of doing this:front to back rendering and z pre-pass.

其中，Pre-Z-Pass使用额外的一个Pass屏蔽颜色的写入，写入深度。

For Z pre-pass, all opaque geometry is rendered in two passes. The first pass populates the Z buffer with depth values from all opaque geometry. A null pixel shader is used and the color buffer is not updated. For this first pass, only simple vertex shading is performed so unnecessary constant buffer updates and vertex-layout data should be avoided. For the second pass, the geometry is resubmitted with Z writes disabled but Z testing on and full vertex and pixel shading is performed. The graphics hardware takes advantage of Early-Z to avoid performing pixel shading on geometry that is not visible.

简单来说，对于所有不透明的物体（透明的没有用，本身不会写深度）。用一个超级简单的Shader进行渲染，这个Shader不写颜色缓冲区，只写深度缓冲区，第二个pass关闭深度写入，开启深度测试，用正常的Shader进行渲染。

毫无疑问，这样做会多出一个Pass的消耗，虽然这个Pass里什么都没有计算，但是还是需要CPU告诉GPU顶点数据等信息。

但Early-Z对于性能的提升往往值得我们使用这个额外的Pass写入深度。

Early-Z技术可以将很多无效的像素提前剔除，避免它们进入耗时严重的像素着色器。Early-Z剔除的最小单位不是1像素，而是像素块（pixel quad，2x2个像素）。

深入剖析GPU Early-Z优化文章对Early-Z进行了更深入的介绍。

3.2 Early-Z失效

Early-Z可以帮助我们将很多无效的像素进行剔除，但也存在很多情况Early-Z会失效，需要图形、引擎程序员特别注意这些情况。

比如下述提到的：

关闭深度测试

• Early-Z是建立在深度测试看开启的条件下，如果关闭了深度测试，也就无法启用Early-Z技术。

Shader写入深度

• 当开启深度写入时，深度会被修改，从而无法进行Early-Z测试。

开启Alpha Test

• 由于Alpha Test需要在像素着色器后面的Alpha Test阶段比较，所以无法在像素着色器之前就决定该像素是否被剔除。

开启Alpha Blend

• 启用了Alpha混合的像素很多需要与frame buffer做混合，无法执行深度测试，也就无法利用Early-Z技术。

开启Tex Kill

• Shader代码中有像素摒弃指令（DX的discard，OpenGL的clip）。

Emil Persson的Depth in Depth文章中提供了一个参考表，列出了在什么情况下Early Z会失效：

四、深度冲突

深度冲突称为Z-Fighting 、Depth-Fighting，是深度缓冲的一个常见问题。

当物体在远处时效果会更明显，因此在远离摄像机的地方，精度不够了，就容易出现两个深度值很接近的片段不断闪烁的问题，看上去就像它们在争夺谁显示在前面的权利。

例如，OpenGL中提到的例子，箱子的底部不断地在箱子底面与地板之间切换，形成一个锯齿的花纹。

4.1 缓解措施

深度冲突不能够被完全避免，但一般会有一些技巧有助于在你的场景中减轻或者完全避免深度冲突。

可采用以下措施来减缓深度冲突：

多边形偏移

永远不要把多个物体摆得太靠近，通过在两个物体之间设置一个用户无法注意到的偏移值，你可以完全避免这两个物体之间的深度冲突。

在箱子和地板的例子中，我们可以将箱子沿着正y轴稍微移动一点。箱子位置的这点微小改变将不太可能被注意到，但它能够完全减少深度冲突的发生。

然而，这需要对每个物体都手动调整，并且需要进行彻底的测试来保证场景中没有物体会产生深度冲突。

近平面调整

尽可能将近平面设置远一些。

在前面我们提到了精度在靠近近平面时是非常高的，所以如果我们将近平面远离观察者，我们将会对整个平截头体有着更大的精度。

然而，将近平面设置太远将会导致近处的物体被裁剪掉，所以这通常需要实验和微调来决定最适合你的场景的近平面距离。

提升硬件精度

牺牲一些性能，使用更高精度的深度缓冲。大部分深度缓冲的精度都是24位的，但现在大部分的显卡都支持32位的深度缓冲，这将会极大地提高精度。所以，牺牲掉一些性能，你就能获得更高精度的深度测试，减少深度冲突。

上述三个技术是最普遍也是很容易实现的抗深度冲突技术了。

然而，上述措施只能减缓深度冲突问题，并不能够完全消除。

4.2 Reverse-Z

深度的精度问题，不得不提到Reverse-Z。

所谓的Reverse-Z是指：

• 近处1.0，远处0.0的深度分布，即NDC深度取值**[0,1]变成[1,0]**。

反向z的实现很简单，只需要：

• 修改投影矩阵，使近平面处的像素映射至NDC下1.0坐标，远平面处像素映射至NDC下的0.0坐标。
• ZTest改为Greater。

使用Reverse-Z的好处：

• 可以使得深度精度变得更高！提高深度值均分分布程度！

为什么呢？

这与浮点数在计算机中的表示和存储方式有关。

根据IEEE标准，浮点数是通过科学计数法来存储的，比如$120.5$用十进制的科学计数法来表示就是$1.25\ast 10^2$。

但是计算机中所有的数据都是按照二进制存储的，所以得先$120.5$转换成为二进制数，即$1.1110001\ast 2^6$。

浮点数在计算机中存储分为三个部分：

1. 符号位（sign）：float和double符号位均为1位，0代表正数，1达标负数。
2. 指数位（exponent）：存储科学计数法中的指数部分，采用移位存储。
3. 尾数位（fraction）：存储科学计数法中的尾数部分。

IEEE 754规定，对于32位的浮点数，最高的1位表示符号，记为s（sign）。接下来8位表示指数记为E（Exponent），剩下的23位有效记作M（fraction）。

• 8位二进制位，能表示的256个数值，由于指数有正有负，标准规定从-127开始计数，也就是-127到128（与有符号数的实现不同），而且-127和128被用作特殊值处理。
• 由于M的整数部分永远是1，我们可以只表示其小数部分记为N。

所以最终表示为：$s\ast 2^E\ast (1+N)$

具体各部分拆解如下，其中$a_0$到$a_{31}$对应32位二进制的值，为0或1。

$$\begin{array}{cc}s=& (-1{)}^{a_0}\\ E=& -127+a_1\times 2^7+a_2\times 2^6+\cdots +a_8\times 2^0\\ N=& a_9\times 2^{-1}+a_{10}\times 2^{-2}+\cdots +a_{31}\times 2^{-23}\end{array}$$

浮点数的精度

精度这里指的是最大有效数字的位数，即只需要考虑尾数部分就可以。

对于float类型，尾数部分是23，转换成10进制的精度，$2^{23}=10^x$，可以求得$x=23log2\approx 6.92$，所以23位2进制最多只能表示6位10进制数。

这里就是C++中头文件中FLT_DIG=6的由来。

当一个浮点数小于1的时候，它可以确保有6位小数位是精确的，也就是说，在$(0,1)$这个开区间内至少可以包含999999（6位）个误差允许的单精度浮点数。

$(1,9)$区间同理，但由于非规约化浮点数（主要是在0值左右）的存在，使得$(0,1)$这个区间内的浮点数个数要比其他这些区间的符点数要多。

在$(10,11)$这个区间内，由于整数位占去了两位，所以这个区间内至少只可以包含99999（5位）个有效单精度浮点数。

以此类推，$(100,101)$开区间内包含9999个有效单精度浮点数，$(1000,1001)$开区间内包含999个有效单精度浮点数等等，当数量级来到$(1000000,1000001)$时(注意这里是闭区间)，这个区间内能保证有效的单精度浮点数不过就两个：1000000与1000001本身。

这说明浮点数的分布与深度值的分布一样是不均匀的，越靠近0的浮点数分布越密集，越远离0的浮点数分布越稀疏：

Depth Precision Visualized提到：

当我们用正常的Z值系统（$[n,f]$映射到$[0,1]$）与浮点数配合时，情况如下：

• z1到z2这么远的距离依然只共享一个深度值0.99。

但当我们将Reversed-Z，（$[n,f]$映射到$[1,0]$）与浮点数配合时，情况发生了变化：

• 深度值Z的降幅越来越小，看似又要陷入精度不够的死胡同，但浮点数的分布规律恰好弥补了这一不足，使得较大的也有足够的精度表示。

反向Z(Reversed-Z)的深度缓冲原理结合数据分析给出了以下结论：

• 传统的近平面映射至0，远平面至1的方法，因为 $Z_{ndc}$ 和 $Z_{view}$ 并非线性映射，再加上浮点数的精度在靠近0的范围聚集两点原因，导致高精度范围完全堆积在了靠近近平面的位置。

• 而使用反向z的方法，利用了上述两个原因互相弥补，进而使得各处的精度都得到保证。

• OpenGL使用的是[-1.0, 1.0]的剪裁范围，无法使用反向z；但是可以通过4.5版本的API修改剪裁范围为[0.0, 1.0]，从而同样可以使用反向z。

五、深度数据的应用

深度缓冲（DepthBuffer）除了用于确定像素的遮挡关系，剔除无用像素的用途之外，还有很多实用的用途。

例如Shadowmap（阴影图）、重建世界坐标等。

下面，将对重建世界坐标进行介绍。

为了求解像素的世界坐标，首先需要确定当前像素投影变换后的NDC坐标。

对于D3D而言：

// depth从深度缓存中采样得到
float3 ComputeWorldPos(float depth)
{
    float4 pos;
    pos.w = 1;
    pos.z = depth;
    // d3d的uv坐标左上为（0,0），右下（1,1）
    pos.x = v_texcoord.x * 2 - 1;
    pos.y = 1- texcoord.y * 2;
    
    // 乘以viewproj矩阵的逆
    float4 worldPos = mul(pos,Inverse_ViewProjMatrix);
    return worldPos.xyz/worldPos .w;
}

对于OpenGL而言：

// depth从深度缓存中采样得到
vec3 ComputeWorldPos(float depth)
{
    vec4 pos;
    pos.w = 1;
    // ndc空间的z为[-1,1]
    pos.z = depth * 2 - 1;
    // opengl的uv坐标左下为（0,0），右上（1,1）
    pos.x = v_texcoord.x * 2 - 1;
    pos.y = v_texcoord.y * 2 - 1;
 
    vec4 worldPos = Inverse_ViewProjMatrix * pos;
    return worldPos.xyz/worldPos .w;
}

参考博文

• 图形学基础之透视校正插值

• 深度缓冲格式、深度冲突及平台差异

• 根据深度重建世界坐标的方式

• OpenGL-Project-Matrix

• OpenGL学习脚印：深度测试(depth testing)

• Unity深度和深度贴图

• 深度缓冲和深度冲突

• D3D投影矩阵

• 容易混淆的Clip Space vs NDC，透视除法

• Unity Shader Early-Z技术

• 深入剖析GPU Early-Z优化

• 反向Z的深度缓冲原理

• IEEE 754 与浮点数的二进制表示

• IEEE754