相机标定（一）-原理及内参、外参

>>>文章索引<<<

相机标定（一）-原理及内参、外参
相机标定（二）-畸变校正，张正友标定法
相机标定（三）-相机成像模型

---

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）。无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

1 坐标系基础

理解四个坐标系是进行相机标定的基础，它们是：

• 图像像素坐标系
• 图像物理坐标系
• 相机坐标系
• 世界坐标系

1.1 图像像素坐标系、图像物理坐标系

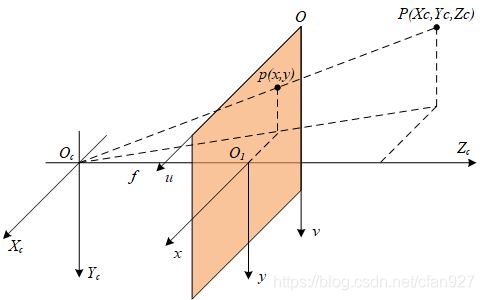
• 图像像素坐标系：是一个二维直角坐标系，反映了相机CCD芯片中像素的排列情况。其原点$O$位于图像的左上角，$u$、$v$坐标轴分别余图像的两条边重合。像素坐标为离散值（0，1，2，…），以像素（pixel）为单位。
• 图像物理坐标系：为了将图像与物理空间相关联，需要将图像转换到物理坐标系下。原点$O$位于图像中心（理想状态下），是相机光轴与像平面的交点（称为主点）。$X$、$Y$坐标轴分别与$u$、$v$轴平行。两坐标系实为平移关系，平移量为$(u_0,v_0)$。

假设相机感光器件中单个像素的物理尺寸为$dX\times dY$，有：

$$\{\begin{array}{l}u=\frac{x}{dX}+u_0\\ v=\frac{y}{dY}+v_0\end{array}\text{\hspace{1em}(1)}$$

把上式写成齐次形式，有：

$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{dX}& 0& u_0\\ 0& \frac{1}{dY}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\text{\hspace{1em}(2)}$$

公式（2）完成了图像物理坐标系到图像像素坐标系的转换。

1.2 相机坐标系

相机坐标系（camera coordinate）$(X_c,Y_c,Z_c)$，也是一个三维直角坐标系，原点位于镜头光心处，$X_c$、$Y_c$轴分别与像面的两边平行，z轴为镜头光轴，与像平面垂直。

点$P(X_c,Y_c,Zc)$为空间中任意一点，其通过投影中心的光线投影到图像平面上，在图像物理空间的投影点为$p(x,y)$，扩展到相机坐标系下其坐标为$(x,y,f)$。根据相似三角形原理，有：

$$\frac{Z_c}{f}=\frac{X_c}{x}=\frac{Y_c}{y}\Rightarrow \{\begin{array}{l}x=f\frac{X_c}{Z_c}\\ y=f\frac{Y_c}{Z_c}\end{array}\text{\hspace{1em}(3)}$$

转为齐次形式为：

$$Z_c\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]\text{\hspace{1em}(4)}$$

公式（4）完成了相机坐标系到图像物理坐标系的转换。

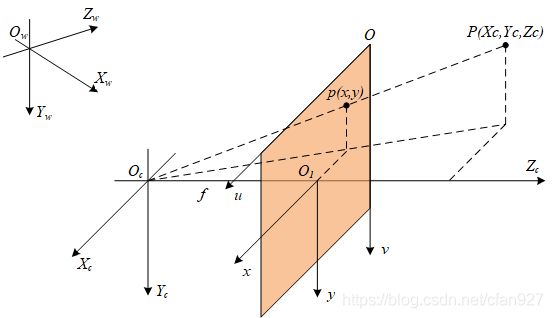
1.3 世界坐标系

世界坐标系（world coordinate）$(X_w,Y_w,Z_w)$，也称为测量坐标系、参考坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。

世界坐标系到相机坐标系的变换，实际上就是一个刚体变换，可以由旋转矩阵$R$和平移矢量$t$来表示。设$(X_w,Y_w,Z_w{)}^T$表示世界坐标系中的点，$(X_c,Y_c,Z_c{)}^T$表示相机坐标系中的点，则它们之间的转换可由下式表示：

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=R\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+t\text{\hspace{1em}(5)}$$

即：

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{3\times 3}& t_{3\times 1}\\ 0_{1\times 3}& 1_{1\times 1}\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\text{\hspace{1em}(6)}$$

公式（6）完成了世界坐标系到相机坐标系的转换。

1.4 世界坐标系到像素坐标系

联立上面的（2）、（4）、（6）式，可以得到世界坐标系与像素坐标系之间的转换关系，有：

$$\begin{array}{rl}{Z}_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]& =\left[\begin{array}{ccc}\frac{1}{dX}& 0& u_0\\ 0& \frac{1}{dY}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\\ & =M_1{M}_2\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\\ & =M\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\end{array}\text{\hspace{1em}(7)}$$

$$M_1=\left[\begin{array}{ccc}\frac{1}{dX}& 0& u_0\\ 0& \frac{1}{dY}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]=\left[\begin{array}{cccc}{f}_x& 0& u_0& 0\\ 0& f_y& v_0& 0\\ 0& 0& 1& 0\end{array}\right]\text{\hspace{1em}(8)}$$

$$M_2=\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\text{\hspace{1em}(9)}$$

其中：

• $M_1$称为相机的内部参数矩阵
• $M_2$称为相机的外部参数矩阵
• $M$称为投影矩阵
• $f_x$、$f_y$分别为相机在x、y轴方向上的归一化焦距，单位为像素，具体解释可以参考这里